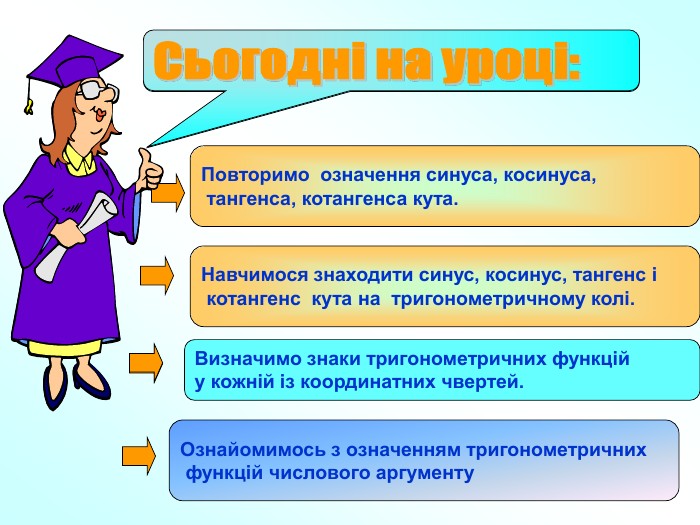
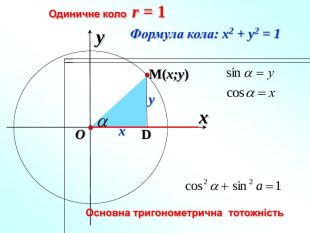
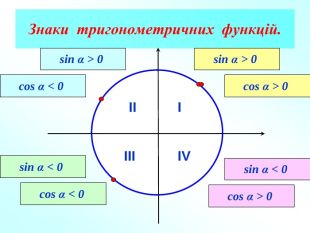
Презентація для уроку з алгебри і початків аналізу 10 клас на тему " Синус, косинус, тангенс кута "
Про матеріал
Презентація для уроку з алгебри і початків аналізу 10 клас на тему " Синус, косинус, тангенс кута " Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Алгебра і початки аналізу (академічний рівень) 10 клас (Мерзляк А.Г., Номіровський Д.А., Полонський В.Б., Якір М.С.)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку



![4. Якщо то кут є кутом… чвертi. 5. Якщо градусна мiра кута дорiвнює 60° [90°], то його радiанна мiра дорiвнює… 6. Якщо градусна мiра кута дорiвнює 270° [45°], то його радiанна мiра дорiвнює… 4. Якщо то кут є кутом… чвертi. 5. Якщо градусна мiра кута дорiвнює 60° [90°], то його радiанна мiра дорiвнює… 6. Якщо градусна мiра кута дорiвнює 270° [45°], то його радiанна мiра дорiвнює…](/uploads/files/193649/271718/295686_images/4.jpg)






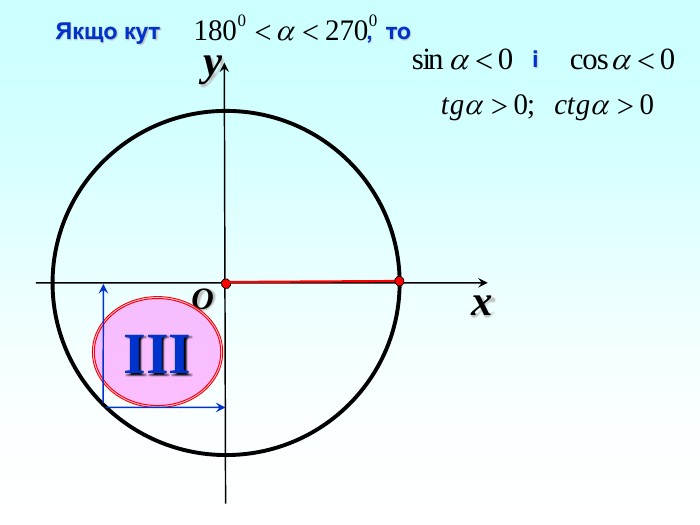
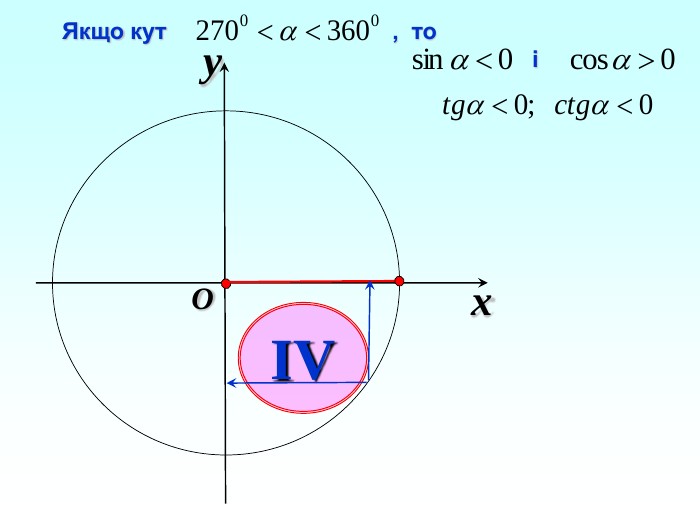







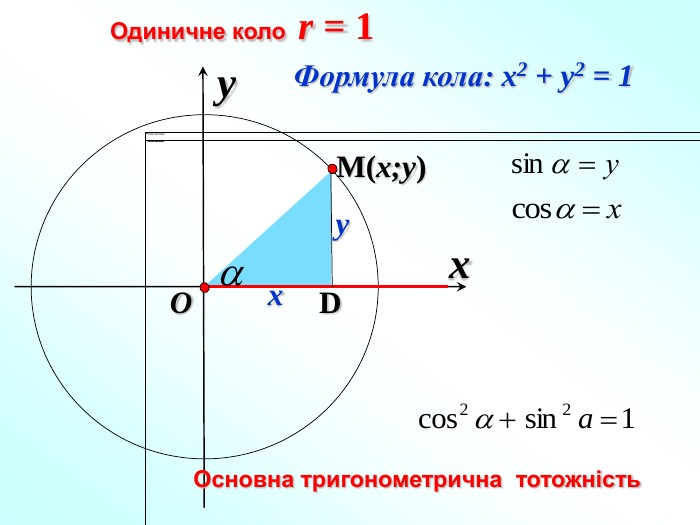







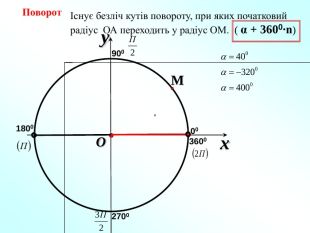
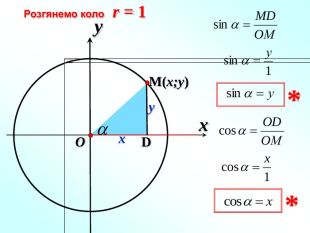
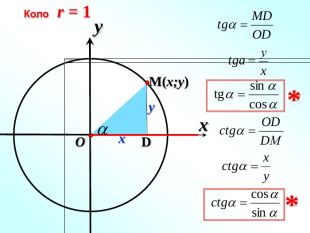


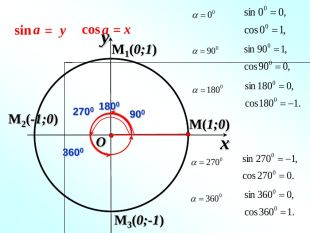



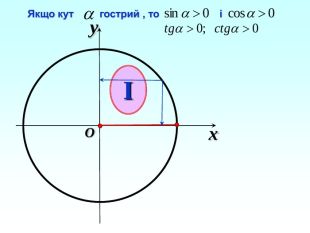
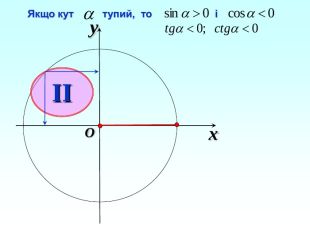
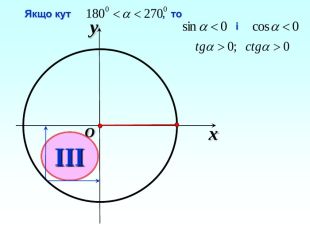
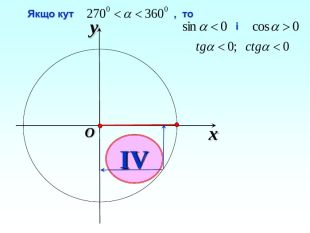








-

Карпович Олег Іванович
09.01.2024 в 11:09
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Самойленко Євгеній
02.05.2023 в 01:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Левадній Сергій Павлович
14.01.2023 в 17:56
Робота виконана на дуже високому рівні!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Базалій Світлана
09.01.2022 в 13:01
Робота виконана на високому рівні користувача ПК.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук