Презентація ,до модуля:"Математичні основи інформатики", на тему: "Нормалізований запис дійсних чисел.Подання чисел з плаваючою комою."

Нормалізований запис дійсних чисел. Подання чисел з плаваючою комою. Підготувала: вчитель інформатики Бойко Оксана Іллівна

Число з плаваючою комою Число з плаваючою комою - форма представлення дійсних чисел, в якій число зберігається у формі мантиси і показника ступеня. При цьому число з плаваючою комою має фіксовану відносну точність і мінливу абсолютну. Найбільш часто використовуване уявлення затверджено в стандарті IEEE 754.

Походження назви. Назва "плаваюча кома" походить від того, що кома в позиційному поданні числа (десяткова кома, або, для комп'ютерів, двійкова кома - далі за текстом просто кома) може бути поміщена де завгодно щодо цифр в рядку. Це положення коми вказується окремо у внутрішньому поданні. Таким чином, подання числа у формі з плаваючою комою може розглядатися як комп'ютерна реалізація експоненційної запису чисел.

Приклад, у формі з фіксованою комою Число, що займає 8 розрядів в цілій частині і 2 розряду після коми, може бути представлено у вигляді 123456,78; 8765,43; 123,00 і так далі. У свою чергу, у форматі з плаваючою комою (у тих же 8 розрядах) можна записати числа 1,2345678; 1234567,8; 0,000012345678; 12345678000000000 і так далі, але для цього необхідно дворозрядне додаткове поле для запису показників ступеня 10 від 0 до 16 10, при цьому загальне число розрядів складе 8 +2 = 10.

Швидкість виконання комп'ютером операцій з числами, представленими у формі з плаваючою комою, вимірюється в мегафлопcах (від англ. FLOPS – число операцій з плаваючою комою в секунду ), гігафлопcах і так далі, і є однією з основних одиниць вимірювання швидкодії обчислювальних систем.

Число з плаваючою комою складається з: Мантиси (що виражає значення числа без урахування порядку) Знака мантиси (що вказує на негативні чи позитивні числа) Порядку (виражає ступінь підстави числа, на яке множиться мантиса) Знака порядку{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}Мантиса. Зсунений порядок. Біт знака8 біт 23 біта Основні формати чисел з плаваючою комою в стандарті IEEE-754: 32-бітовий формат

Нормальна форма і нормалізована форма. Перевага використання представлення чисел у форматі з плаваючою комою над виставою у форматі з фіксованою комою (і цілими числами) полягає в тому, що можна використовувати істотно більший діапазон значень при незміннійвідносної точності.

Нормальна форма числа Нормальною формою числа з плаваючою комою називається така форма, в якій мантиса (без урахування знака) знаходиться на полуінтервале [0; 1) (0≤a<1). Число з плаваючою комою, що знаходиться не в нормальній формі, втрачає точність у порівнянні з нормальною формою.

Така форма запису має недолік:деякі числа записуються неоднозначно (наприклад, 0,0001 можна записати у 4 формах - 0,0001 10 0, 0,001 10 -1, 0,01 10 -2, 0,1 10 -3), тому поширена (особливо в інформатиці) також інша форма запису - нормалізована, в якій мантиса десяткового числа приймає значення від 1 (включно) до 10 (невключно), а мантиса двійкового числа приймає значення від 1 (включно) до 2 (не включно) (1≤a

Так як старший розряд (ціла частина числа) мантиси двійкового числа (крім «0») в нормалізованому вигляді дорівнює "1", то при записі мантиси числа в ЕОМ старший розряд можна не записувати, що і використовується в стандарті IEEE 754. Впозиційних системах числення з підставою більшим, ніж 2 (в троичной, четверичной та ін), цієї властивості немає.

Запис у формі з плаваючою комою Запис у формі з плаваючою комою схожа на запис чисел у стандартному вигляді, але мантиса і експонента записуються роздільно. Мантиса записується в нормалізованому форматі - з фіксованою комою, після першої значущої цифри. Наприклад, період обігу (на орбіті) супутника планети Юпітера Іо, який дорівнює 152853,5047 с, в стандартному вигляді можна записати як 1,528535047 *10 5с. Приклад запису у формі з плаваючою комою буде 1528535047 з показником 5. Це означає, що записане число в 10 5 разів більше числа 1,528535047, тобто для отримання подразумеваемого числа кома зсувається на 5 розрядів вправо.

Запис числа у формі з плаваючою комою дозволяє робити обчислення над широким діапазоном величин, поєднуючи фіксована кількість розрядів і точність. Наприклад, у десятковій системі надання чисел з плаваючою комою (3 розряду) операцію множення, яку ми б записали як 0,12 0,12 = 0,0144 в нормальній формі представляється у вигляді (1,20 10 -1) (1,20 10 -1) = (1,44 10 -2). У форматі з фіксованою комою ми б отримали вимушене округлення 0,120 0,120 = 0,014. Ми втратили крайній правий розряд числа, так як даний формат не дозволяє коми "плавати" по запису числа.

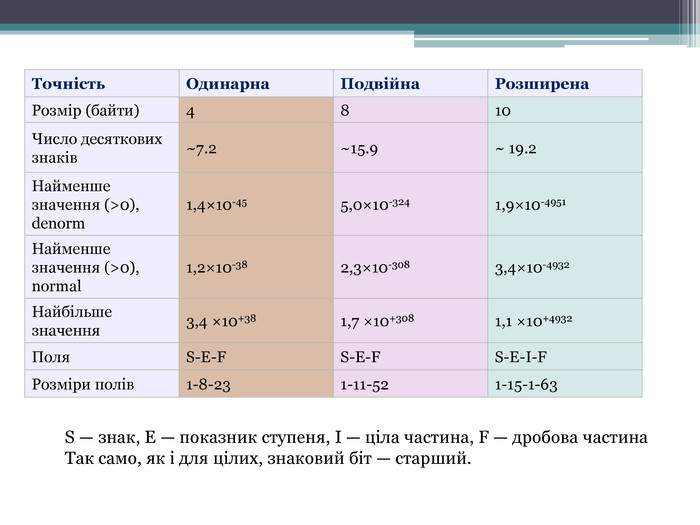
Діапазон чисел, представлених у форматі з плаваючою комою. Діапазон чисел, які можна записати даними способом, залежить від кількості біт, відведених для представлення мантиси і показника. На звичайній 32-бітної обчислювальній машині, що використовує подвійну точність (64 біта), мантиса становить 1 біт знак + 52 біта, показник - 1 біт знак + 10 біт. Таким чином отримуємо діапазон точності приблизно від 4,94 10 -324 до 1.79 10 308 (від 2 -522 - 1022 до ~ 1 2 1024).

Точність. Одинарна. Подвійна. Розширена. Розмір (байти)4810 Число десяткових знаків~7.2~15.9~ 19.2 Найменше значення (>0), denorm1,4×10-455,0×10-3241,9×10-4951 Найменше значення (>0), normal1,2×10-382,3×10-3083,4×10-4932 Найбільше значення3,4 ×10+381,7 ×10+3081,1 ×10+4932 Поля. S-E-FS-E-FS-E-I-FРозміри полів1-8-231-11-521-15-1-63 S — знак, E — показник ступеня, I — ціла частина, F — дробова частина. Так само, як і для цілих, знаковий біт — старший.

Приклад Записати двійкове число в нормалізованій формі формату із рухомою комою:11101,011=00.11101011∙25=00.11101011.00.0101. При нормалізації число зсувають вправо (якщо є ціла частина числа) або вліво (до одиниці після коми). При зсуві вправо, порядок (тобто степінь основи) збільшується з кожним зсувом на 1. При зсуві вліво порядок зменшується щораз на 1.

Для прийнятого формату це число запишеться як:01234567891011121314150011101011000101

При запису мантиси зручно, щоб старший розряд мантиси і порядку був ліворуч. Іноді розташування старшого розряду визначають окремо. Приклад запису числа із від’ємним знаком порядку. N=00.00011111;Nm=00.11111∙2-3=00.11111000.11.0011 Оскільки основа q=2(10)=010(2)завжди постійна, то її запис у характеристиці числа опускається. Діапазон поданих чисел визначається розрядною сіткою автомата.

Діапазон поданих чисел визначається розрядною сіткою автомата. Максимальне число буде при позитивних знаках мантиси і порядку і при максимальних значеннях їх чисел, тобто, коли у всіх розрядах будуть одиниці. Мінімальне число має негативні знаки мантиси і порядку, при максимальному значенні мантиси і порядку (одиниці по всіх розрядах). Nmax=(00.111…1)∙2111…1, Nmin=(11.111…1)∙2-111…1 При використанні формату з рухомою комою, швидкість обчислень падає, але точність і діапазон подання чисел зростає.