Презентація ,до модуля:"Математичні основи інформатики", на тему: "Основні поняття позиційної і непозиційної системи числення.Позиційні і непозиційні системи числення в історії "

Основні поняття позиційної і непозиційної системи числення. Позиційні і непозиційні системи числення в історії людства. Підготувала: вчитель інформатики Бойко Оксана Іллівна

Сукупність прийомів та правил найменування й позначення чисел називається системою числення. Звичайною для нас і загальноприйнятою є позиційна десяткова система числення.

Непозиційна cистема числення. Система числення, в якій значення кожної цифри в довільному місці послідовності цифр, яка означає запис числа, не змінюється, називається непозиційною. Наприклад, непозиційною системою числення є римська нумерація, в якій використовуються такі знаки або цифри для позначення чисел: І -1, У – 5, Х – 10, L – 50, C – 100, D – 500, M – 1000 тощо.

Позиційна cистема числення. Система числення, в якій значення кожної цифри залежить від місця в послідовності цифр у записі числа, називається позиційною. Щоб визначити число, недостатньо знати тип і алфавіт. Добре відомим прикладом непозиційної системи числення є римська система, в якій роль цифр відіграють букви алфавіту: І – один; V – п’ять; Х – десять; С – сто; L – п’ятдесят; D – п’ятсот; М – тисяча.

Десяткова позиційна система числення. Загальноприйнятою в сучасному світі є десяткова позиційна система числення, яка з Індії через арабські країни прийшла в Європу. Основою цієї системи є число десять. Основою системи числення називається число, яке означає, у скільки разів одиниця наступного розрядку більше за одиницю попереднього. Число у цій системі числення можна представити у вигляді степенів десяти, наприклад:23710 = 2·102+3·101 + 7·100

Позиційна cистема числення. Перша позиційна система числення виникла понад 2000 років до н.е. в стародавньому Вавилоні. Це була шістдесяткова позиційна нумерація. Проте принцип позиційного значення цифр тут ще не використовувався скрізь. Винахід позиційної системи числення приписують шумерам, а подальший розвиток – індусам. Ідея позиційної системи числення була описана ще Архімедом у роботі«Обчислення піску».

Позиційна cистема числення. Позиційна СЧ складається з обмеженої кількості цифр, проте позиція кожної цифри у числі забезпечує значимість (вагу) цієї цифри. Позиція цифри на мові математики називається розрядом. Тобто значення цифри «мінливе» і залежить від її позиції в числі. Наприклад, у 10-й СЧ, в числі 33 дві трійки мають різне значення: права трійка означає цифру 3 (кількість одиниць), а ліва – число 30 (кількість десятків).

Позиційна cистема числення. Для позиційних систем числення характерні наочність зображення чисел і відносна простота виконання арифметичних операцій. Саме позиційні системи числення стали основою сучасної математики. Будь-яке натуральне число можна зобразити у довільній позиційній системі числення і до того ж єдиним чином.

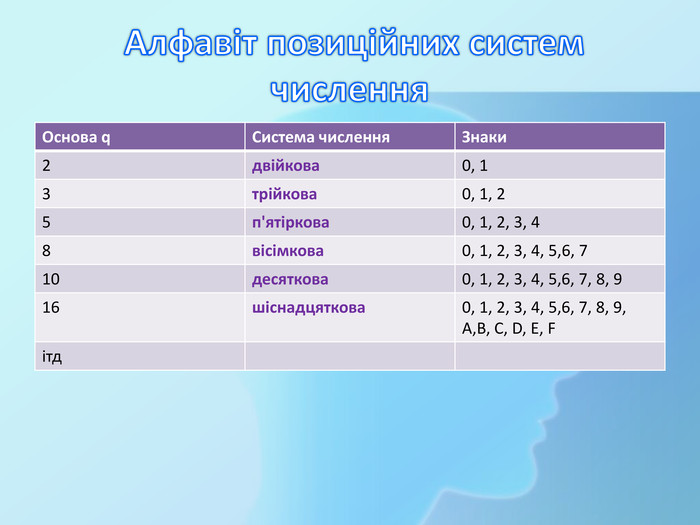
Алфавіт позиційних систем числення{00 A15 C55-8517-42 AA-B614-E9 B94910 E393}Основа q. Система числення. Знаки2двійкова0, 13трійкова0, 1, 25п'ятіркова0, 1, 2, 3, 48вісімкова0, 1, 2, 3, 4, 5,6, 710десяткова0, 1, 2, 3, 4, 5,6, 7, 8, 916шіснадцяткова0, 1, 2, 3, 4, 5,6, 7, 8, 9, A,B, C, D, E, Fітд

Приклад Числа трійкової СЧ будуть наступними: 0, 1, 2, 10, 11, 12, 20, 21,22…Для зазначення основи системи, до якої належить число, вводять індексне позначення: 7510 , 10112 , 2 А716 , 548.

Приклад. Приклади запису чисел: двійкова СЧ, q=2; ai Є {0,1}, A2 =1012 =1*2 2 +0*2 1*2 0вісімкова СЧ, q=8; aiЄ{0,1...7}, A8 =1758 =1*1082 + 7*10 81+5*1080+1*8 =7*8 101 +5*8100 , тобто 108=810 десяткова СЧ, q=10; aiЄ{0,1...9}, A10=531,2610 =5*102 +3*10 1+ 1*100 +2*10-1 +6*10 -2 =500=30+1+0,20+0,06