Презентація до уроку на тему:"Особливості реалізації дійсночисельної комп'ютерної арифметики"
Про матеріал
Інформатика. Вибірковий модуль. Презентація до уроку на тему:"Особливості реалізації дійсночисельної комп'ютерної арифметики"
Особливості додавання чисел, представлених у формі з плаваючою комою. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку














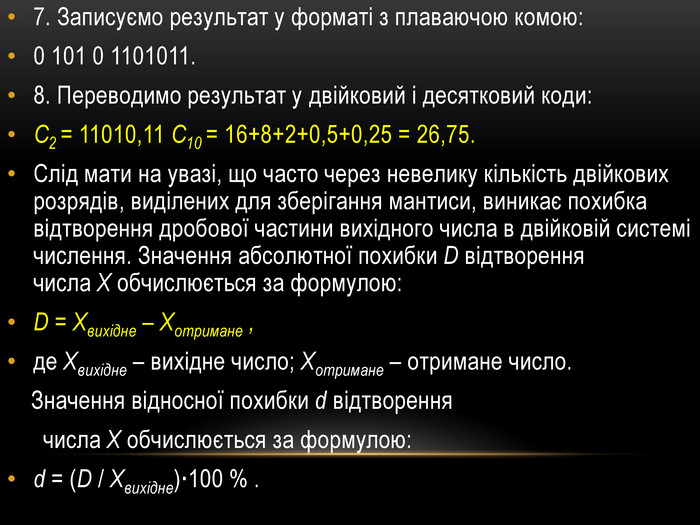
![Приклад А10 = 6,25, В10 = 20,51. Записуємо числа в двійковому коді: А2 = 110,01 = 0.11001·2+3 В2 = 10100,1 = 0.101001·2+52. Записуємо числа у форматі з плаваючою комою:[А]пк = 0 011 0 11001[В]пк= 0 101 0 101001 Приклад А10 = 6,25, В10 = 20,51. Записуємо числа в двійковому коді: А2 = 110,01 = 0.11001·2+3 В2 = 10100,1 = 0.101001·2+52. Записуємо числа у форматі з плаваючою комою:[А]пк = 0 011 0 11001[В]пк= 0 101 0 101001](/uploads/files/63663/118877/130225_images/16.jpg)
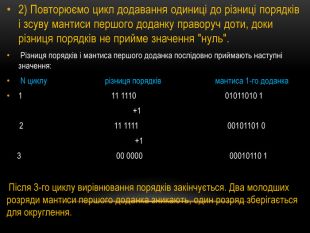
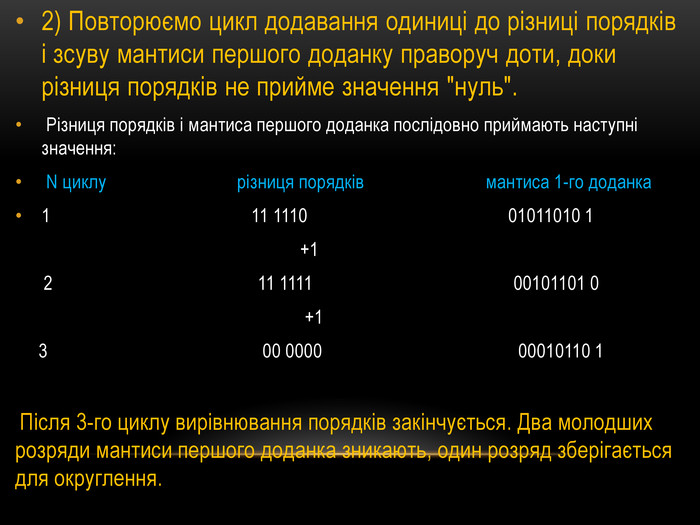
![3. Порівнюємо порядки: РВ – РА = 5 – 3 = 2.4. Різниця порядків не дорівнює нулю, тому виконуємо вирівнювання порядку числа A і відповідну корекцію мантиси числа A (порядок числа А менше порядку числа В на 2, тому робимо зсув мантиси числа А на два розряди вправо і збільшуємо порядок числа А на 2):[А]пк = 0 101 0 0011001[В]пк= 0 101 0 101001 3. Порівнюємо порядки: РВ – РА = 5 – 3 = 2.4. Різниця порядків не дорівнює нулю, тому виконуємо вирівнювання порядку числа A і відповідну корекцію мантиси числа A (порядок числа А менше порядку числа В на 2, тому робимо зсув мантиси числа А на два розряди вправо і збільшуємо порядок числа А на 2):[А]пк = 0 101 0 0011001[В]пк= 0 101 0 101001](/uploads/files/63663/118877/130225_images/17.jpg)
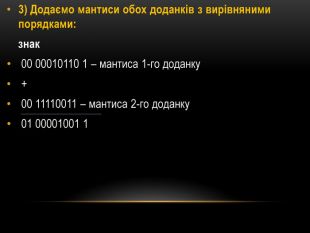
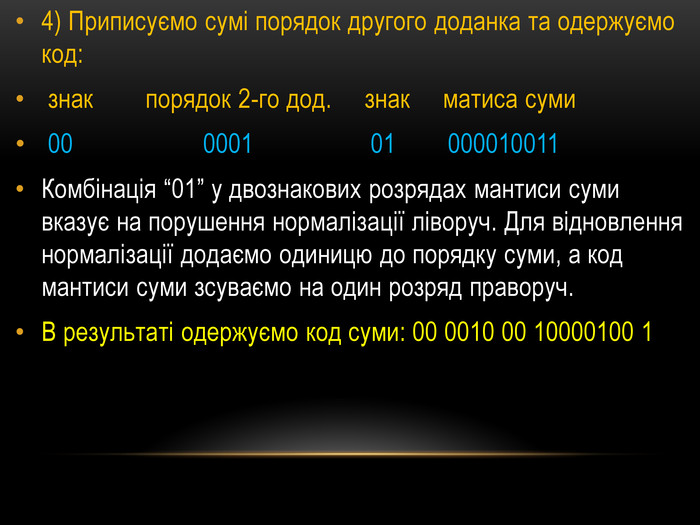
![5. Вирівнюємо кількість двійкових розрядів у мантисах чисел А і В (розрядна сітка мантиси числа В на одиницю менша, тому в мантису числа Bдописуємо один нуль справа):[А]пк = 0 101 0 0011001[В]пк= 0 101 0 10100106. Виконуємо операцію додавання мантис у додатковому модифікованому коді (знаки мантис відображаємо двома двійковими розрядами):[МА]дк = 00 0011001+[МВ]дк = 00 1010010[МС]дк = 00 1101011 Мантиса результату додавання не потребує нормалізації, тому що розряди знака мають однакові значення і значення старшого розряду мантиси не дорівнює значенню молодшого розряду знака. 5. Вирівнюємо кількість двійкових розрядів у мантисах чисел А і В (розрядна сітка мантиси числа В на одиницю менша, тому в мантису числа Bдописуємо один нуль справа):[А]пк = 0 101 0 0011001[В]пк= 0 101 0 10100106. Виконуємо операцію додавання мантис у додатковому модифікованому коді (знаки мантис відображаємо двома двійковими розрядами):[МА]дк = 00 0011001+[МВ]дк = 00 1010010[МС]дк = 00 1101011 Мантиса результату додавання не потребує нормалізації, тому що розряди знака мають однакові значення і значення старшого розряду мантиси не дорівнює значенню молодшого розряду знака.](/uploads/files/63663/118877/130225_images/18.jpg)