Презентація до позакласного заходу з математики "Цікаві способи усної математичної лічби"

Цікаві числа та способи математичної лічби

Особливості числа 1729 Дивне число 142857 Цікавий добуток чисел, утворених з одиниць. Множення чисел записаних за допомогою дев’яток. Таблиця чисел, утворених із вісімок. Спосіб округлення у швидкісній лічбіШвидкі способи множення десяткових чисел. Російський спосіб усної лічби Італійський спосіб усної лічбиІндійський спосіб усної лічби Відомі постаті,що володіли швидкісною лічбою

Особливості числа 1729 Цікавим є натуральне число 1729. Про нього можна сказати ,що це найменше натуральне число , яке можна подати у вигляді суми кубів двома різними способами :1729=13 +123 (1+1728)1729=93 + 103 (729+1000)Меншого натурального числа , яке має такі властивості не існуєОсобливість числа 1729 помітив також Масахіко Фуджівара. Він довів , що якщо знайти суму цифр цього числа і отримане число помножити на його дзеркальне відображення , то отримане число знову 1729.1 + 7 + 2 + 9=1919 * 91 =1729 Фуджівара довів , що чисел із такими властивостями всього 4 : 1729, 81, 1, 145881 = 8 + 1 =99*9 = 811 + 4 + 5 + 8=1818*81 = 14581 = 11*1 = 1

Дивне число 142857 Ще одним цікавим числом є 142857. У ньому при множенні просто міняються цифри місцями :142857 * 1 = 142857142857 * 2 = 285714142857 * 3 = 428571142857 * 4 = 571428142857 * 5 = 714285142857 * 6 = 857142 А при множенні цього числа 7:142857 * 7 = 999999 , а ще цікаво , що 142 + 857 = 999 і 14 + 28 + 57 = 99 1 + 4 + 2 + 8 + 5 + 7 = 27 =2+7 =9. А також 1428572 = 20408122449, до того ж 20408 + 122499 = 142857

Цікавий добуток чисел, утворених з одиниць. Досліджуючи добутки чисел можна побачити і такий результат:111111111 * 111111111 = 12345678987654321 У ході досліджень також було виявлено , що числа складені з одиниць також дають ряд цікавих співвідношень . Наприклад : 11 * 11 – 10 * 1 * 1 = 111 111 * 111 – 10 *11 * 11 = 11111 1111 * 1111 – 10 * 111 * 111 =1111111 11111 * 11111 – 10 * 1111 * 1111 = 11111111 і т. д. Цей ряд можна продовжувати безкінечно . А пояснити отримані результати можна таким чином : 11* 11 =121 10 * 1 *1 = 10 , 121 – 10 = 111. 111 * 111 = 12321 10 * 11 * 11= 1210, 12321 – 1210 = 11111. 1111 * 1111= 1234321 111 * 111 = 123210, 1234321- 123210 = 111111111.

Множення чисел записаних за допомогою дев’яток. При вивченні таблички множення на 9 зручно користуватися 10 пальцями рук. Наприклад , щоб 3*9 починаючи із великого пальця лівої руки відраховуємо 3 палець ( бо множимо на 3) і загинаємо його у долоню . Тоді зліва від нього кількість пальців , що показує десятки у добутку , а справа одиниці тобто 3 * 9 = 27. На цю таблицю множення дуже схожою є таблиця множення числа складеного з дев’ яток:99 * 2 = 198 999 * 2 = 199899 * 3 = 297 999 * 3 = 299799 * 4 = 396 999 * 4 = 399699 * 5 = 495 999 * 5 = 499599 * 6 = 594 999 * 6 = 599499 * 7 = 693 999 * 7 = 699399 * 8 = 792 999 * 8 = 799299 * 9 = 891 999 * 9 = 8991   9999 * 2 = 19998 9999 * 3 = 29997 9999 * 4 = 39996 9999 * 5 = 49995 9999 * 6 = 59994 9999 * 7 = 69993 9999 * 9 = 89991 Цікаво , що коли виконувати множення 99999 * 2 = 199998 99999 * 3 = 299997 99999 * 4 = 399996 і т.д. Можна помітити особливість цих добутків . В результаті множення 5-и цифрового числа , кожна цифра якого 9, на множник 4 – отримаємо число . Перша і остання цифри цього числа 3 і 6 ( бо 4 * 9 = 36 ) а між ними знаходяться ще 4 цифри – дев’ятки І продовжувати знаходження подібних добутків чисел складених із 9 можна до безкінечності.

Спосіб округлення у швикісній лічбі Для швидкого усного обчислення суми чисел можна використовувати спосіб округлення . Ось у чому його суть : Якщо один з доданків , округлюючи збільшити на кілька одиниць , то отриману суму треба зменшити на стільки ж одиниць: 251 + 368 = 251 + 370 -2 = 621 – 2 =619 364 + 391 = 364 + 400 – 9 = 764 – 9 =755 Якщо один доданок зменшити на кілька одиниць , а інший доданок на стільки ж одиниць збільшити , то сума не зміниться: 697 + 546 = 700 + 543 = 1243 Якщо при відніманні від’ємник збільшуємо на кілька одиниць , то і зменшувати також треба на стільки ж одиниць збільшити: 1574 – 995 = 1579 – 1000 = 579 Якщо при обчисленні зменшуване зменшити на кілька одиниць, то отриманий результат потрібно збільшити на цю кількість одиниць: 954 – 252 = 952 - 252 +2 = 702 1076 - 378 = 1068 - 378 + 8 = 718

Швидкість думки можна розвинути за допомогою. Усна лічба. Швидке читання. Пам’ять

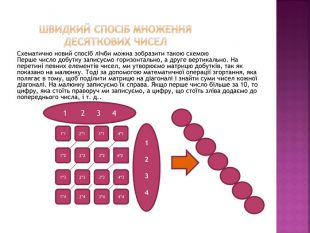
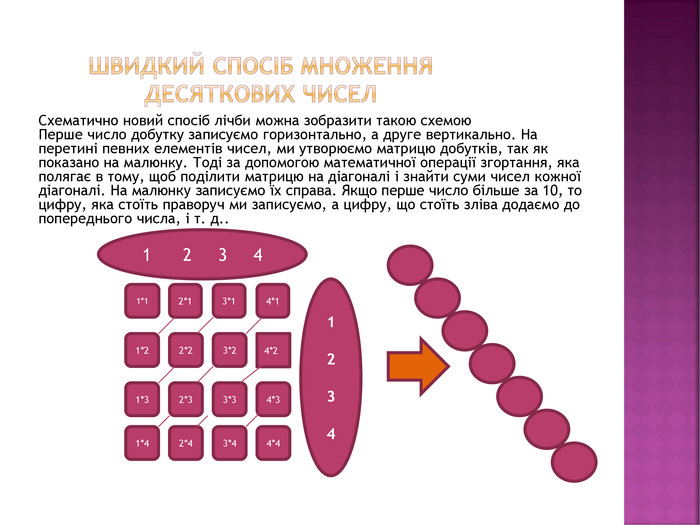
Швидкий спосіб множення десяткових чисел. Схематично новий спосіб лічби можна зобразити такою схемою. Перше число добутку записуємо горизонтально, а друге вертикально. На перетині певних елементів чисел, ми утворюємо матрицю добутків, так як показано на малюнку. Тоді за допомогою математичної операції згортання, яка полягає в тому, щоб поділити матрицю на діагоналі і знайти суми чисел кожної діагоналі. На малюнку записуємо їх справа. Якщо перше число більше за 10, то цифру, яка стоїть праворуч ми записуємо, а цифру, що стоїть зліва додаємо до попереднього числа, і т. д..1 2 3 4 12341*12*13*14*14*23*22*21*24*33*32*31*31*42*43*44*4

Знайдемо добуток 754*326 Матриця добутків. Отже, 754*326=245804{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}754*211512314108242302462438642921

Графічний спосіб лічби Множити десяткові числа можна й іншим способом. Він полягає в тому, щоб зображати цифрі, з яких складаються множники у вигляді ліній. Наприклад, 34*45 . Для цього цифри десятків та одиниць першого множника запишемо горизонтальними прямими, а другого множника – вертикальними прямими.12 15  16 20 Потрібно порахувати кількість перетинів у кожному куточку. Записуємо отримані суми з кінця таким чином 20, далі суму 16+15, тоді 12. Отже, 123120. Число 3 додаємо до 12, буде 15, а 1 додаємо до 2, отримаємо 3. Очікуваний добуток – 1530.

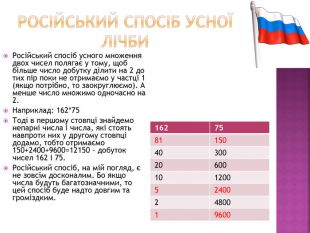
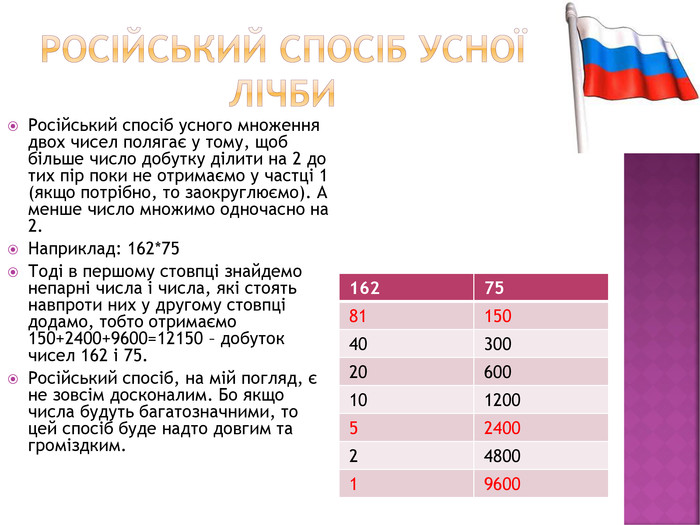
Російський спосіб усної лічби{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}16275811504030020600101200524002480019600 Російський спосіб усного множення двох чисел полягає у тому, щоб більше число добутку ділити на 2 до тих пір поки не отримаємо у частці 1 (якщо потрібно, то заокруглюємо). А менше число множимо одночасно на 2. Наприклад: 162*75 Тоді в першому стовпці знайдемо непарні числа і числа, які стоять навпроти них у другому стовпці додамо, тобто отримаємо 150+2400+9600=12150 – добуток чисел 162 і 75. Російський спосіб, на мій погляд, є не зовсім досконалим. Бо якщо числа будуть багатозначними, то цей спосіб буде надто довгим та громіздким.

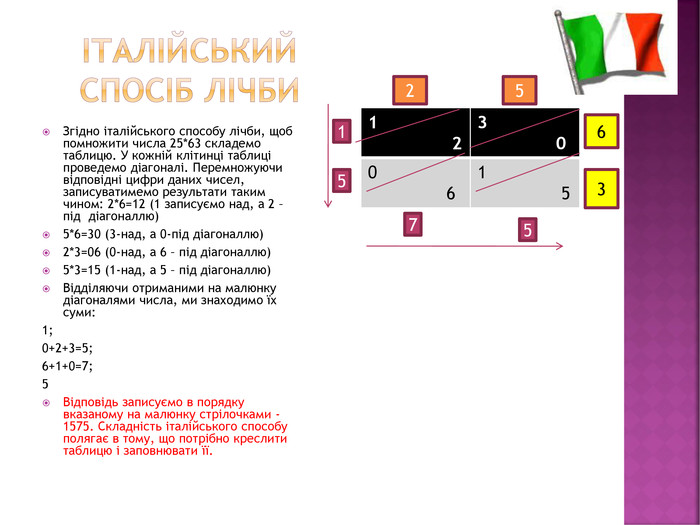
Італійський спосіб лічби. Згідно італійського способу лічби, щоб помножити числа 25*63 складемо таблицю. У кожній клітинці таблиці проведемо діагоналі. Перемножуючи відповідні цифри даних чисел, записуватимемо результати таким чином: 2*6=12 (1 записуємо над, а 2 –під діагоналлю)5*6=30 (3-над, а 0-під діагоналлю)2*3=06 (0-над, а 6 – під діагоналлю)5*3=15 (1-над, а 5 – під діагоналлю)Відділяючи отриманими на малюнку діагоналями числа, ми знаходимо їх суми:1;0+2+3=5;6+1+0=7;5 Відповідь записуємо в порядку вказаному на малюнку стрілочками - 1575. Складність італійського способу полягає в тому, що потрібно креслити таблицю і заповнювати її.{5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}{073 A0 DAA-6 AF3-43 AB-8588-CEC1 D06 C72 B9}1 2 3 00 61 515572563

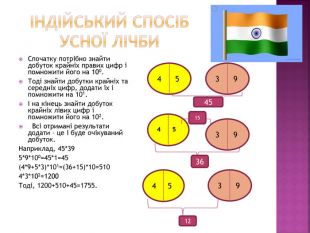
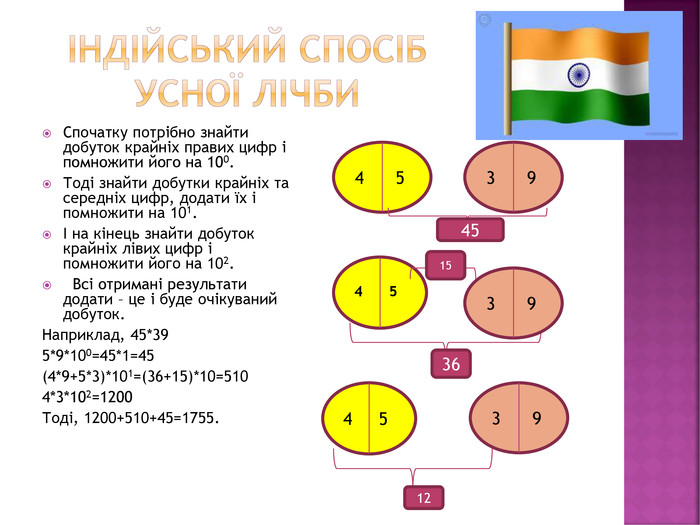
Індійський спосіб усної лічби. Спочатку потрібно знайти добуток крайніх правих цифр і помножити його на 100. Тоді знайти добутки крайніх та середніх цифр, додати їх і помножити на 101.І на кінець знайти добуток крайніх лівих цифр і помножити його на 102. Всі отримані результати додати – це і буде очікуваний добуток. Наприклад, 45*395*9*100=45*1=45(4*9+5*3)*101=(36+15)*10=5104*3*102=1200 Тоді, 1200+510+45=1755.4 5 3 94 5 3 94515364 53 912

Відомі постаті, що володіли швидкісною лічбою Серед відомих особистостей, котрі володіли швидкою усною лічбою є Джордж Паркер Бідер, Шакунтала Деві та Деніел Мак. Картні. Джордж Паркер Бідер будучи маленьким хлопчиком дивував оточуючих своїми унікальними математичними здібностями. Батько прозвав його «рахуючий хлопчик». Пізніше він здобув освіту і займався розвитком мережі залізничних доріг у Англії. Бідер міг з одного разу запам’ятати будь-які 43 числа і за 6 хвилин перемножував дев’ятизначні числа між собою.

Шакунтала Деві з дитинства виступала у батьківському цирку. З 3 років дивувала всіх лічильними карточними фокусами, а в майбутньому обігрувала досвіченних граків. Вона могла добути корінь 21 степеня з 220-значного числа. Деніел Мак. Картні був дивовижною людиною. Від народження він був сліпий, але за 10 хвилин міг піднести число 29 до 6-го степеня, а за 3 хвилини знайшов кубічний корінь з семизначного числа. До того ж він володів феноменальною пам’ятю і міг розказати в деталях про будь-який день свого життя.

Математику ніколи не пізно почати вчити і любити. Адже ця наука дуже багатогранна, захоплююча і цікава. В математиці завжди можна для себе відкрити щось нове та нерозгадане, випробувати свої знання і можливо, зробити відкриття