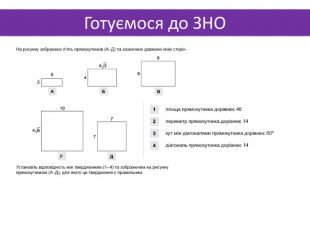
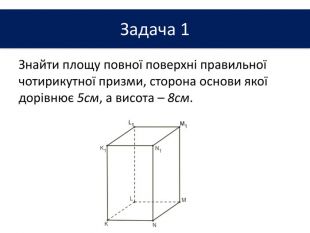
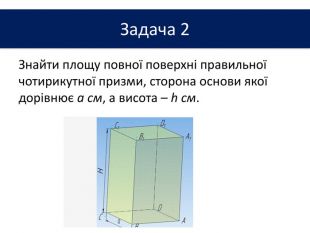
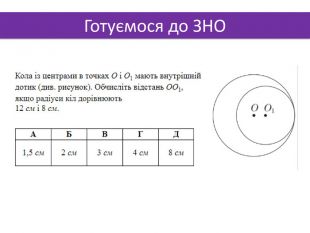
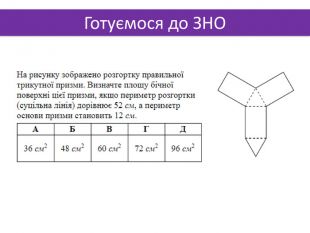
Презентація до теми "Многогранники"

Готуємося до ЗНО

Тема: Двогранні кути. Лінійний кут двогранного кута

Двогранним кутом називається фігура, утворена двома півплощинами α та β зі спільною прямою МN, що їх обмежує. Півплощини α та β називають гранями двогранного кута. Пряму МN, що їх обмежує, - ребром двогранного кута. αβм. N

ADCHКут між площинами АСН та СНD – це двогранний кут АСНD, де СН ребро. Точки А та D лежать на гранях цього кута. FAF⊥CH, FD ⊥CH. Тоді кут AFD називають лінійний кут двогранного кута АCHD 

Всі лінійні кути двогранного кута рівні один одному. АВOА1 В1 O1 Промені ОА та О1 А1 – співнапрямлені. Промені ОВ та О1 В1 – співнапрямлені. Кути АОВ та А1 О1 В1 рівні, як кути зі співнапрямленими сторонами. Двогранні кути можна порівнювати: більший той, у якого більший лінійний кут.

кут РОК – лінійний кут двогранного кута РDEК. DEГрадусною мірою двогранного кута називається градусна міра його лінійного кута. PDEK = POKАЛГОРИТМ ПОБУДОВИ ЛІНІЙНОГО КУТАDOРК

Двогранний кут може бути гострим, прямим, тупим

Двогранні кути можуть бути суміжними і вертикальними ПИТАННЯ: Дано двогранний кут, міра якого 52. Чому дорівнює міра суміжного з ним двогранного кута?Вертикального?

Півплощина, яка обмежена ребром двогранного кута і ділить його на два рівні двогранні кути, називається бісекторною півплощиною, або бісектором двогранного кута. ПИТАННЯ: Чому дорівнює двогранний кут між бісекторами двох суміжних двогранних кутів?

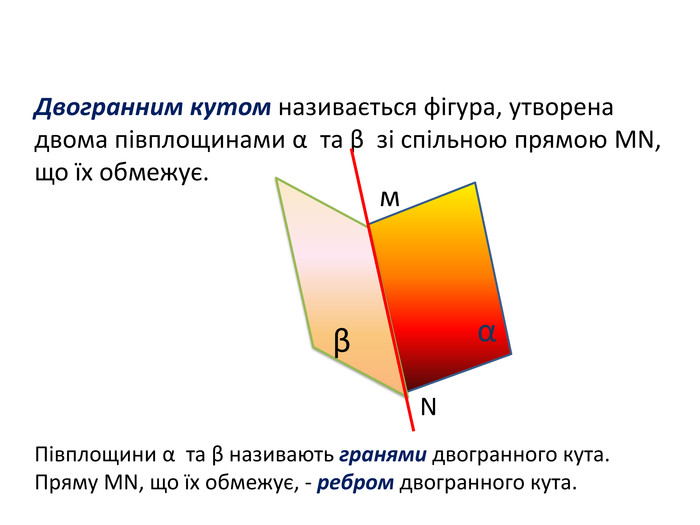
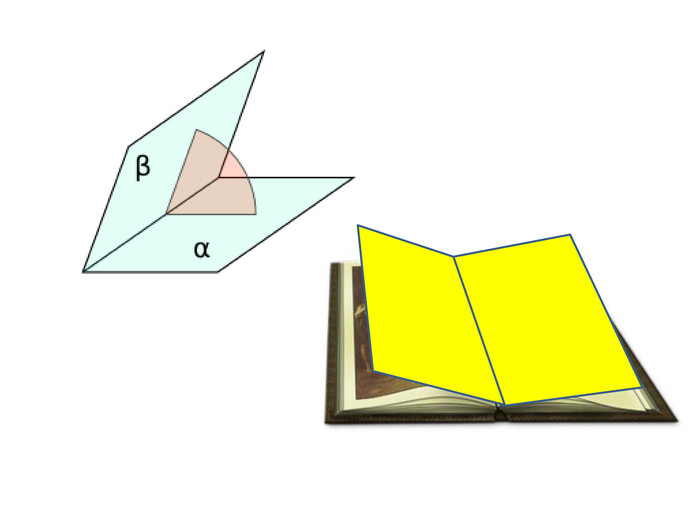
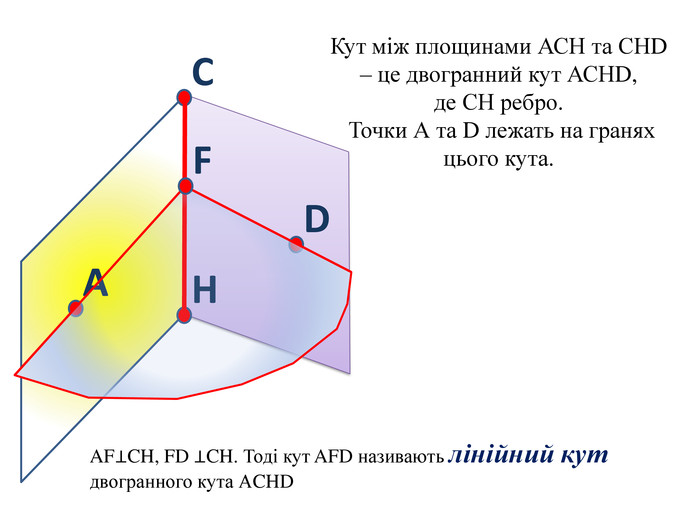
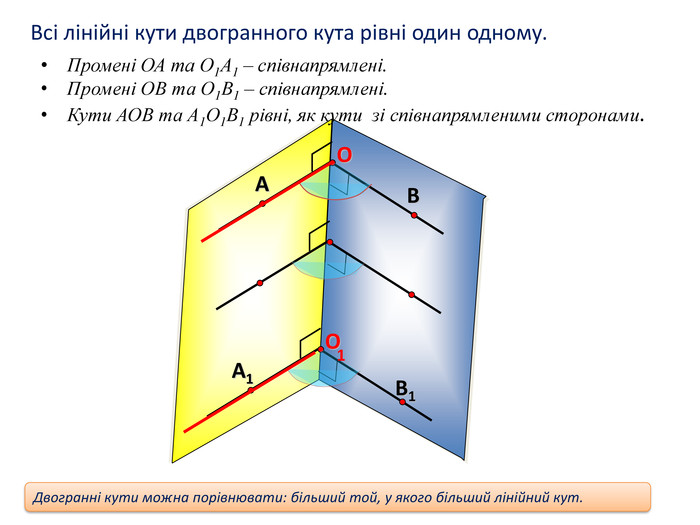
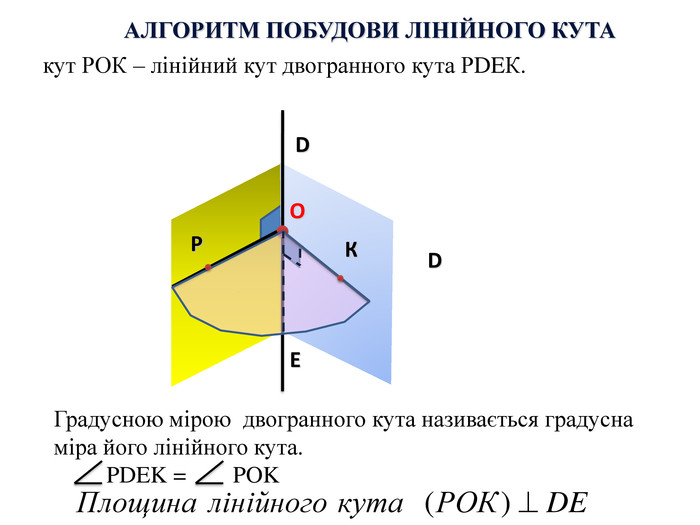
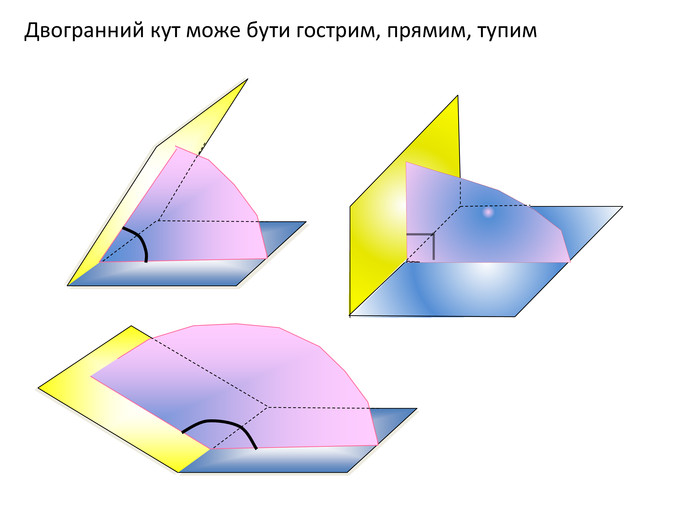
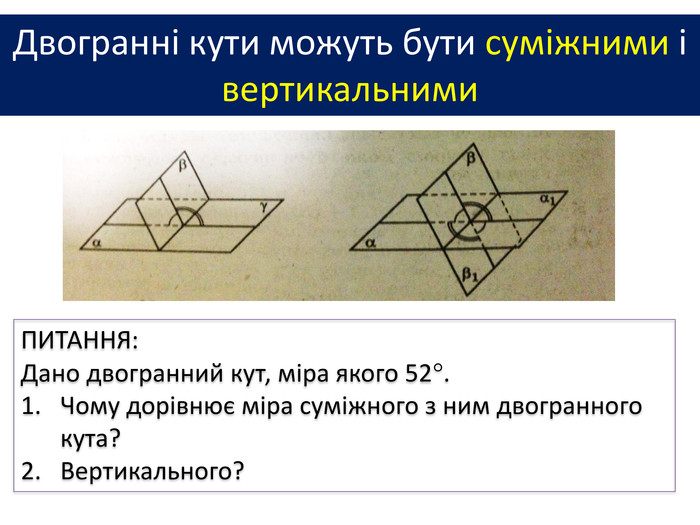
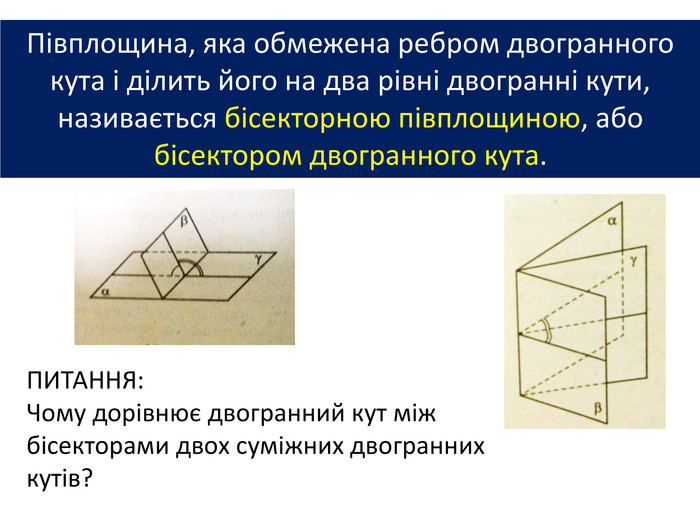
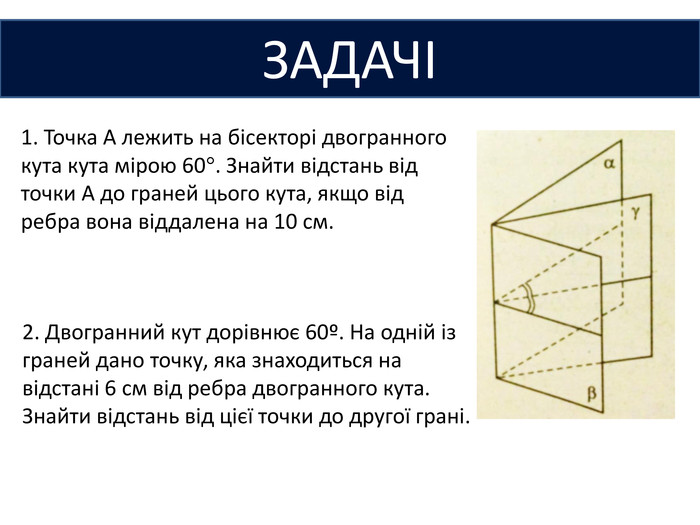
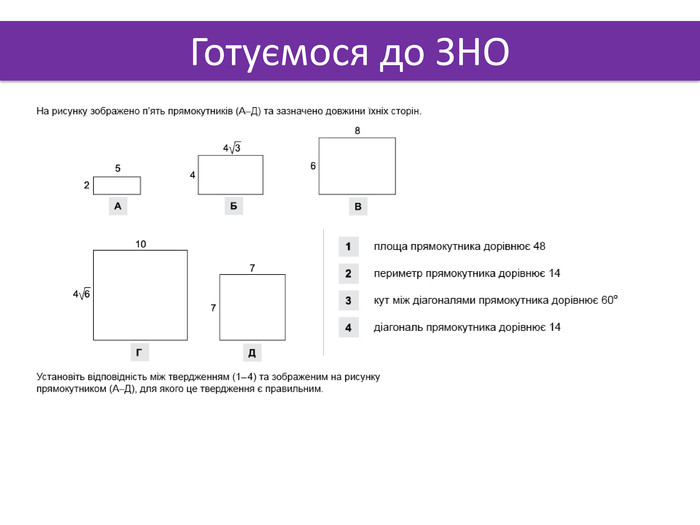
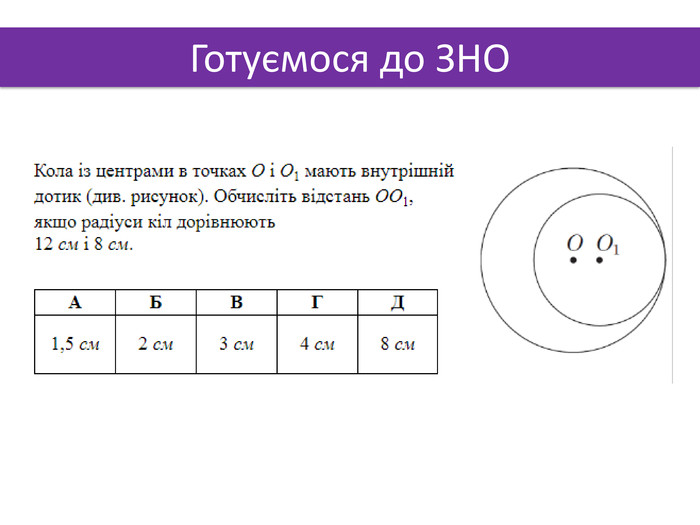
1. Точка А лежить на бісекторі двогранного кута кута мірою 60. Знайти відстань від точки А до граней цього кута, якщо від ребра вона віддалена на 10 см.2. Двогранний кут дорівнює 60º. На одній із граней дано точку, яка знаходиться на відстані 6 см від ребра двогранного кута. Знайти відстань від цієї точки до другої грані. ЗАДАЧІ

Готуємося до ЗНО

Готуємося до ЗНО

Тема: Многогранник та його елементи. Опуклі многогранники

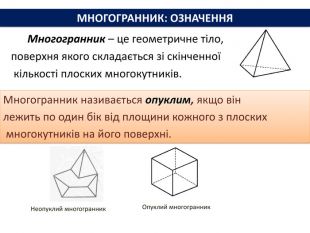
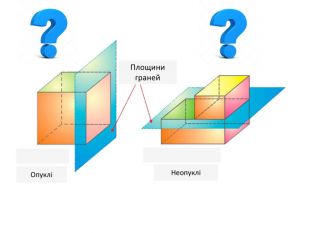
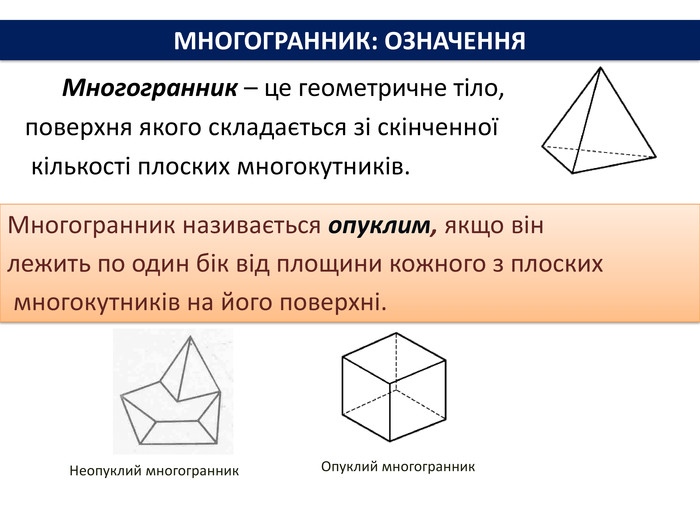
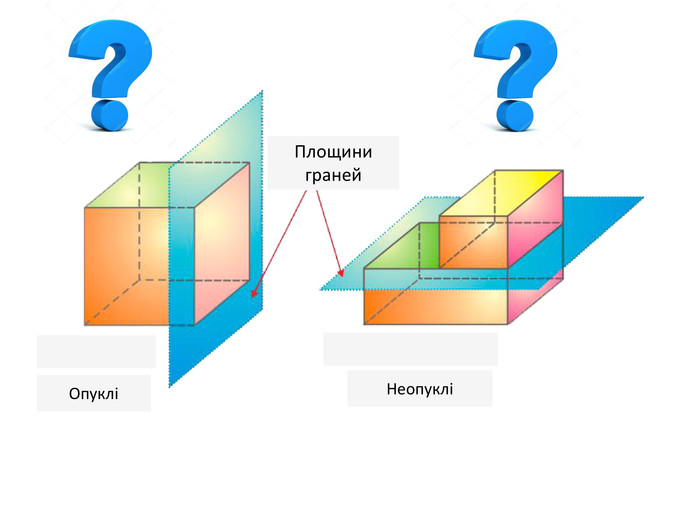
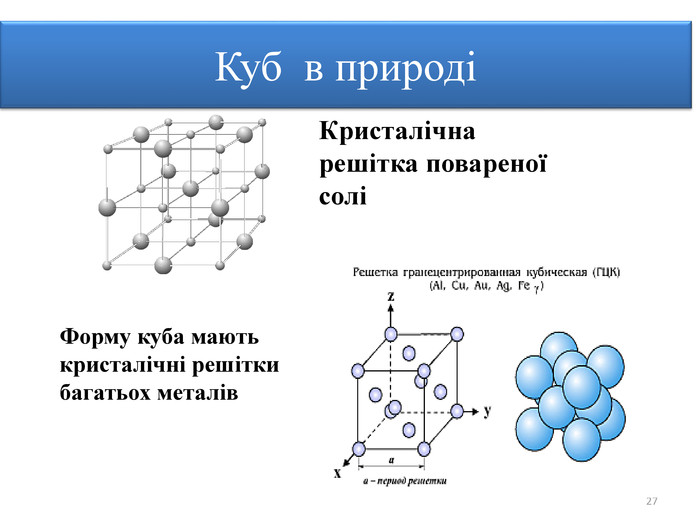
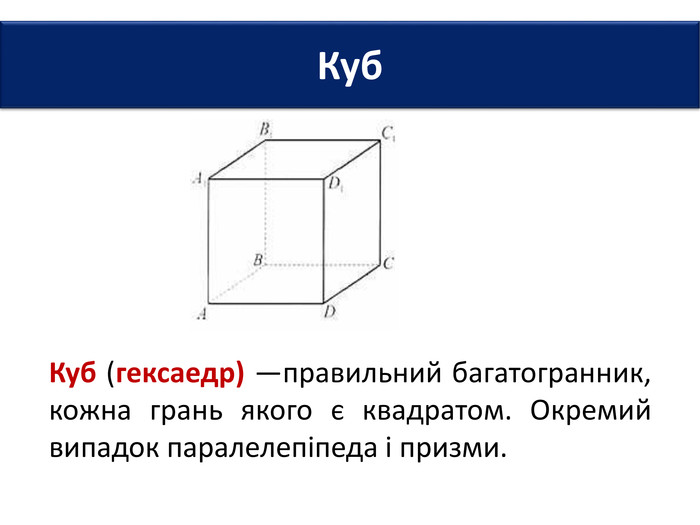
Многогранник – це геометричне тіло, поверхня якого складається зі скінченної кількості плоских многокутників.  Многогранник називається опуклим, якщо він лежить по один бік від площини кожного з плоских многокутників на його поверхні. Неопуклий многогранник. Опуклий многогранник. МНОГОГРАННИК: ОЗНАЧЕННЯ

Площини граней. ОпукліНеопуклі

Спільна частина площини і поверхні опуклого многогранника називається гранню. Грані опуклого многогранника є плоскими опуклими многокутниками. Сторони граней називаються ребрами многогранника, а вершини - вершинами многогранника. МНОГОГРАННИК: ЕЛЕМЕНТИ

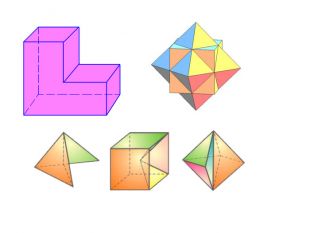
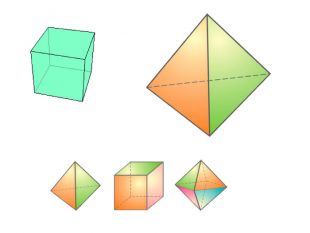
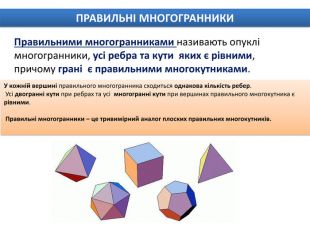
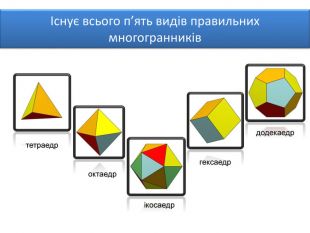
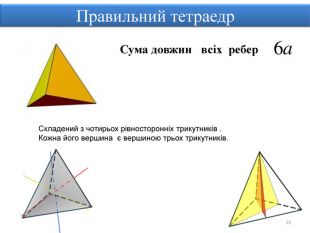
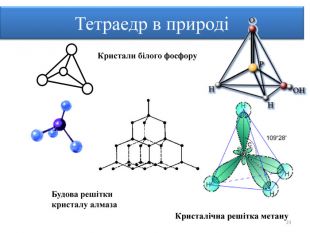
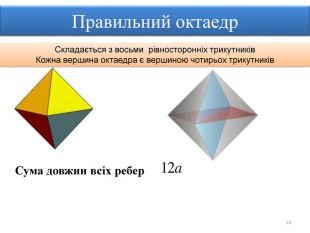
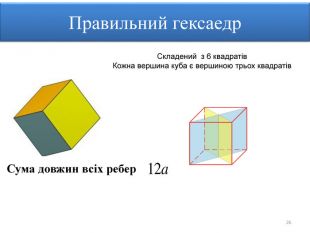
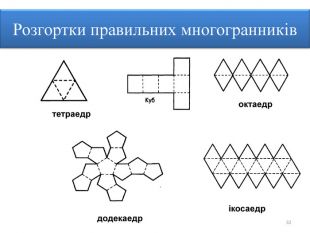
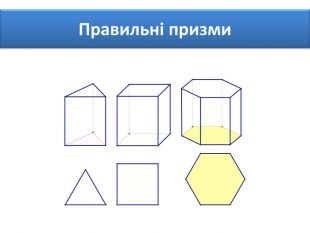
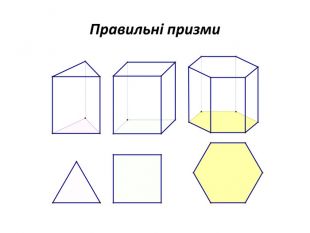
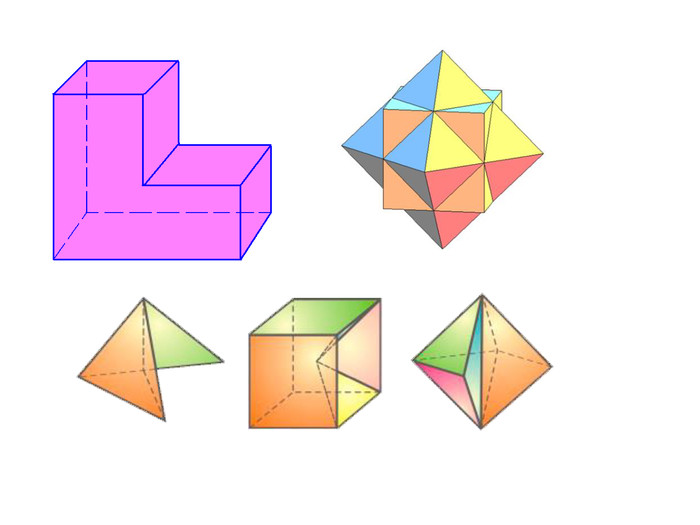
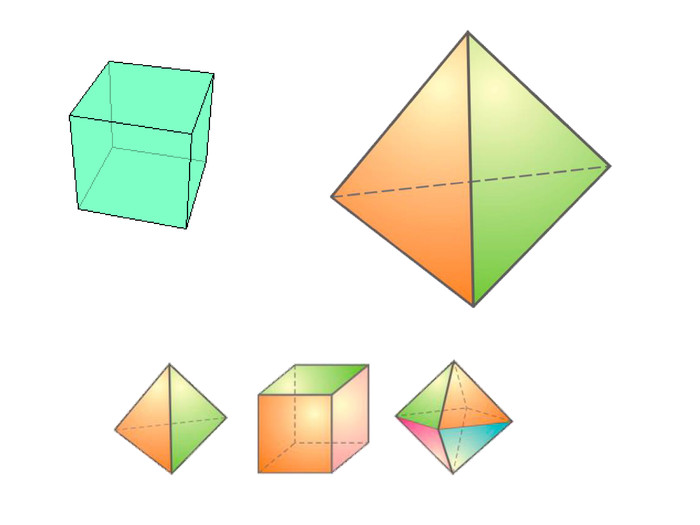
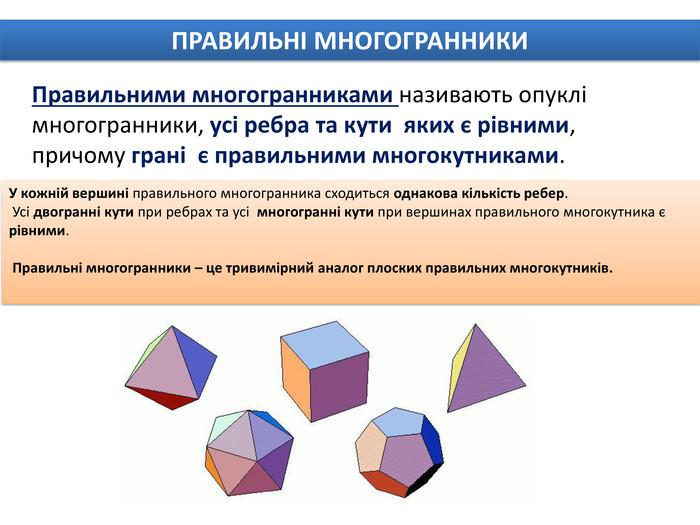
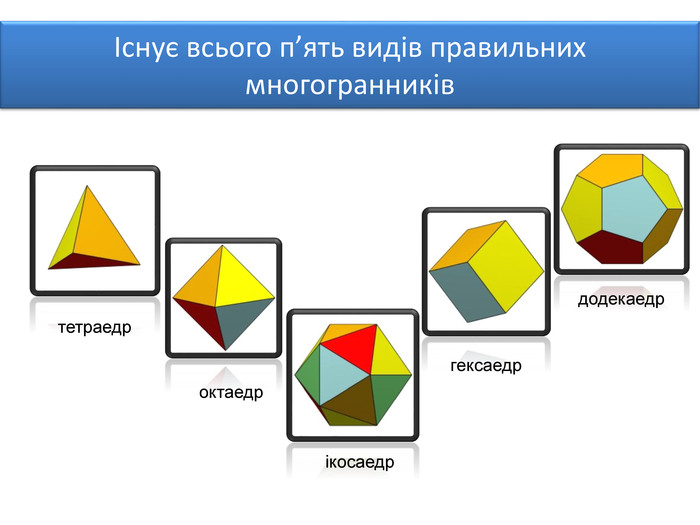
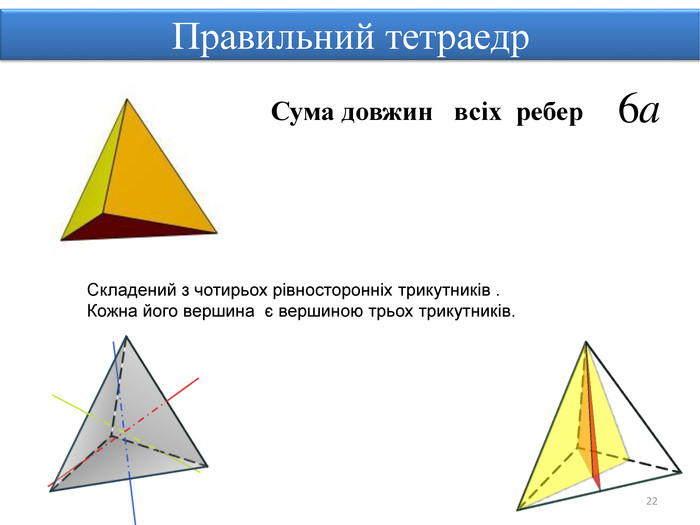
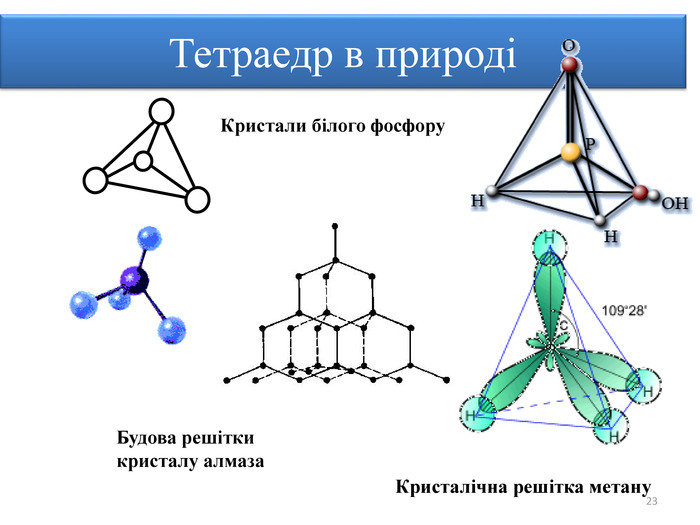
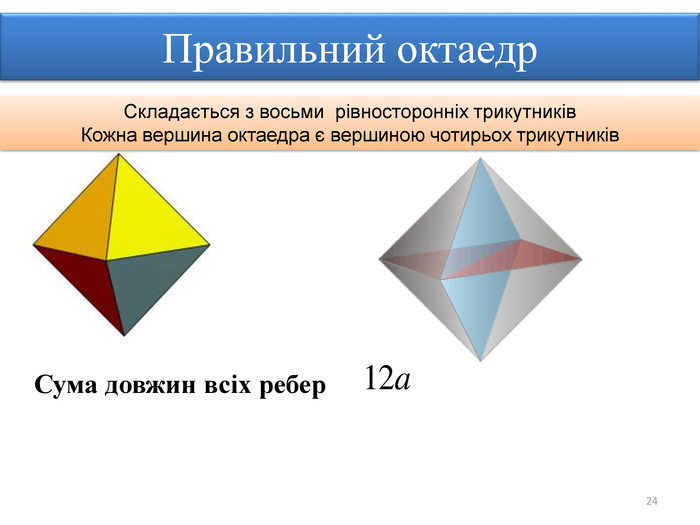
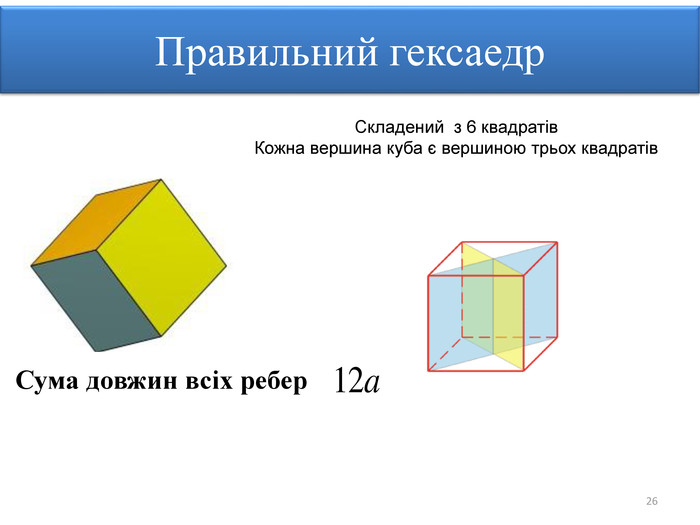
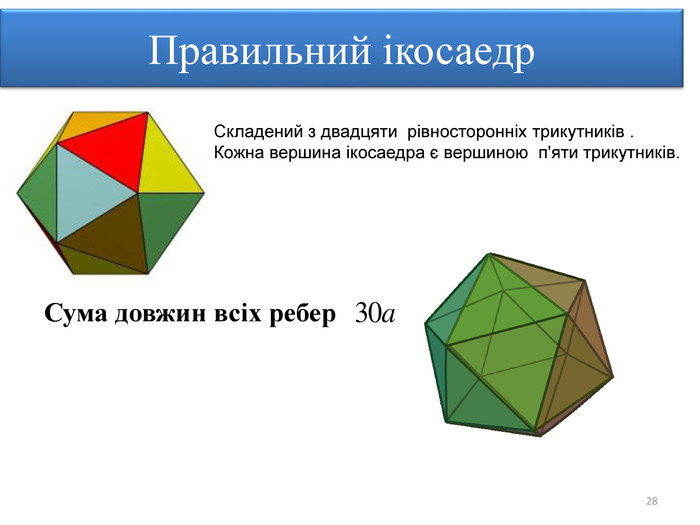
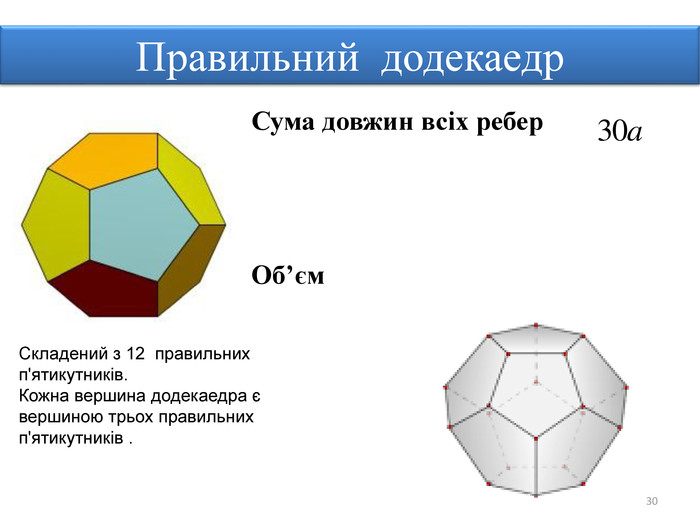
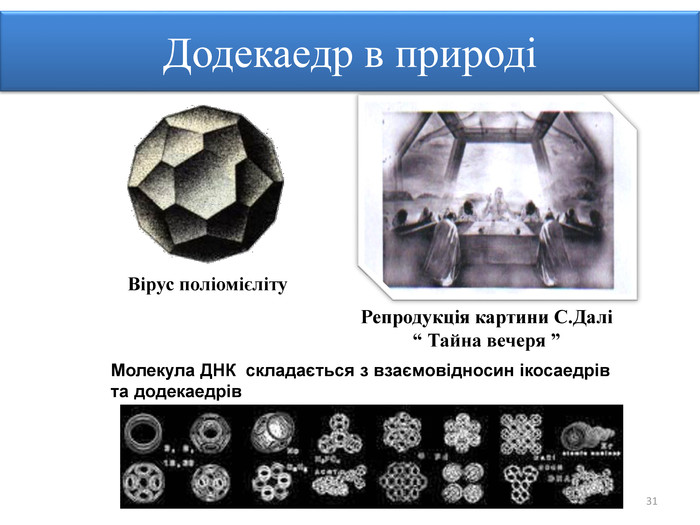
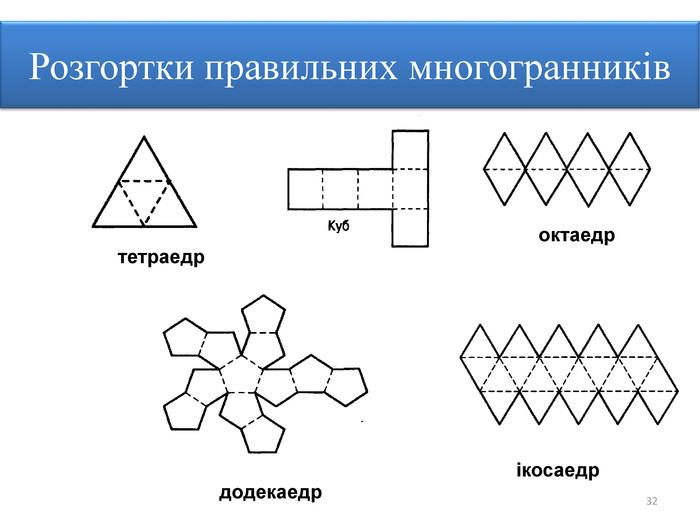
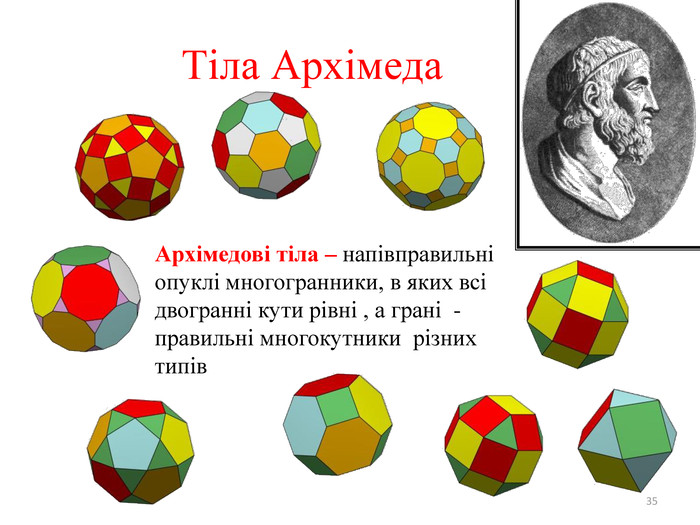
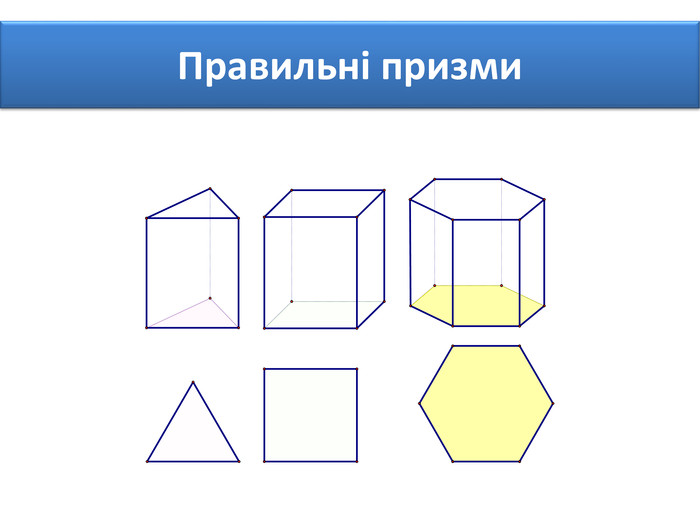
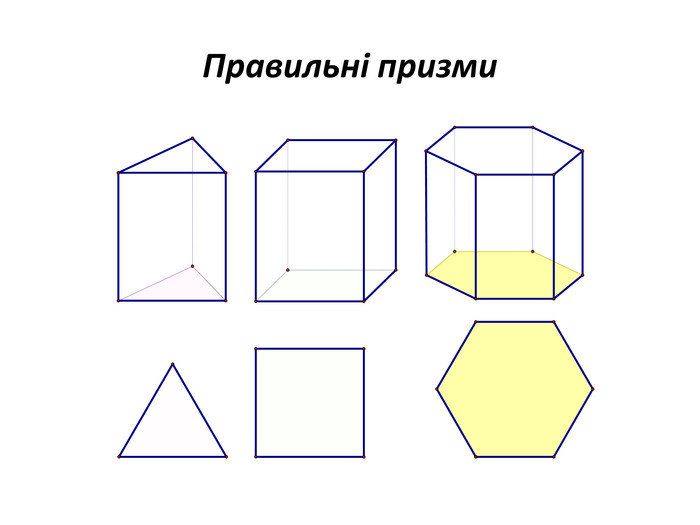
Правильними многогранниками називають опуклі многогранники, усі ребра та кути яких є рівними, причому грані є правильними многокутниками. ПРАВИЛЬНІ МНОГОГРАННИКИУ кожній вершині правильного многогранника сходиться однакова кількість ребер.  Усі двогранні кути при ребрах та усі многогранні кути при вершинах правильного многокутника є рівними.  Правильні многогранники – це тривимірний аналог плоских правильних многокутників. 

Існує всього п’ять видів правильних многогранників тетраедроктаедрікосаедргексаедрдодекаедр

Правильний тетраедр22 Сума довжин всіх ребер Складений з чотирьох рівносторонніх трикутників . Кожна його вершина є вершиною трьох трикутників.

Тетраедр в природі23 Кристали білого фосфору. Будова решітки кристалу алмаза. Кристалічна решітка метану

Правильний октаедр24 Сума довжин всіх ребер. Складається з восьми рівносторонніх трикутників Кожна вершина октаедра є вершиною чотирьох трикутників

Октаедр в природі25 Вуглець С характеризується структурою октаедра. Кристали алмаза

Правильний гексаедр26 Сума довжин всіх ребер. Складений з 6 квадратів Кожна вершина куба є вершиною трьох квадратів

Куб в природі27 Кристалічна решітка повареної соліФорму куба мають кристалічні решітки багатьох металів

Правильний ікосаедр28 Сума довжин всіх ребер. Складений з двадцяти рівносторонніх трикутників . Кожна вершина ікосаедра є вершиною п'яти трикутників.

Ікосаедр в природі29 Кристал бору має форму ікосаедра. У біології німецький біолог початку ХХ століття Еге Геккель дослідив,що одноклітинні організми – феодарії, точно передають форму ікосаедра. У фізиці капсиди багатьох вірусів (наприклад бактеріофаги, мімівірус)

Правильний додекаедр30 Сума довжин всіх ребер. Об’єм Складений з 12 правильних п'ятикутників. Кожна вершина додекаедра є вершиною трьох правильних п'ятикутників .

Додекаедр в природі31 Вірус поліомієліту. Молекула ДНК складається з взаємовідносин ікосаедрів та додекаедрів. Репродукція картини С. Далі“ Тайна вечеря ”

Розгортки правильних многогранників32тетраедроктаедрікосаедрдодекаедр

Платон вважав, що світ будується з чотирьох «стихій» – вогню, землі, повітря і води, атоми цих «стихій» мають форму чотирьох правильних многогранників, а п’ятий же многогранник символізував Всесвіт

34вогонь тетраедр вода ікосаедр повітря октаеэдр земля гексаедр всесвіт додекаедр

Тіла Архімеда35 Архімедові тіла – напівправильні опуклі многогранники, в яких всі двогранні кути рівні , а грані - правильні многокутники різних типів

Тіла Пуансона36 Малий зірковий додекаедр. Великий зірковий додекаедр. Великий додекаедр. Великий ікосаедр

ПРИЗМА

Призма. Многогранник, складений із двох рівних многокутників A1 A2 ... An і B1 B2 ... Bn, розташованих в паралельних площинах, і n паралелограмів, називається призмоюstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Многокутники A1 A2 ... An і B1 B2 ... Bn називаються основами призми,а паралелограми– бічними гранями призми

Бічні ребра призмивідрізки A1 B1, A2 B2, … , An. Bn називаються бічними ребрами призми. Бічні ребра призми рівні і параллельніstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Призму з основами A1 A2 ... An і B1 B2 ... Bn позначають A1 A2 ... An. B1 B2 ... Bn і називають n-кутною призмоюstyle.colorfillcolorfill.type

ПРИЗМА: ЕЛЕМЕНТИосновавершинибічні гранібічні ребра (висота)

Висота призми. Перпендикуляр, проведений з якої-небудь точки одної основи до площині іншої основи, називається висотою призмиstyle.colorfillcolorfill.type

Пряма і похила призми. Якщо бічні ребра призми перпендикулярні до основи, то призма називається прямою, в іншому випадку - похилою Висота прямої призми дорівнює її бічному ребруstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Правильна призма. Пряма призма називається правильною, якщо в її основі - правильні багатокутники Властивість правильної призми. У правильної призми всі бічні грані - рівні прямокутникиstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Правильні призми

ПРИЗМА: площа бічної поверхні (бп), повної поверхні (пп)𝑺пп=𝑺бп+𝟐∙𝑺осн 𝑺бп=𝑷осн∙𝑯 

ПРИЗМА

Діагоналі призми. Діагоналлю призми називається відрізок, який сполучає дві вершин призми, що не належать одній граніstyle.colorfillcolorfill.type

Діагональні перетини призми. Перетини призми площинами, що проходять через два бічних ребра, які не належать одній грані, називаються діагональними перерізами Діагональні перетини призми називаються паралелограмами

Діагональні перетини призми

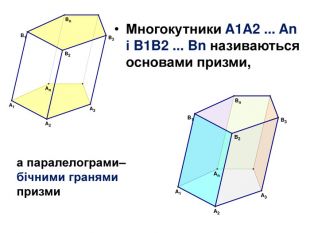
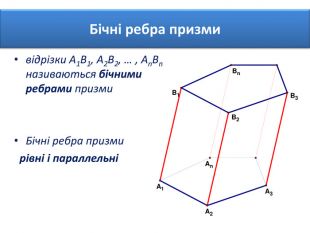
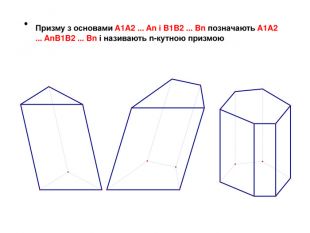
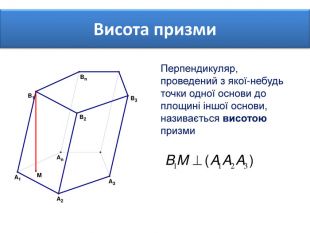
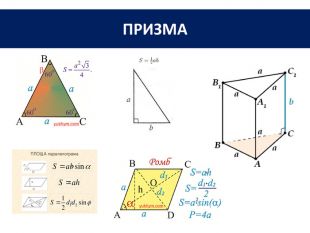
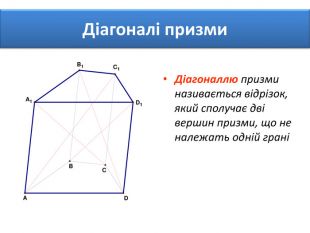
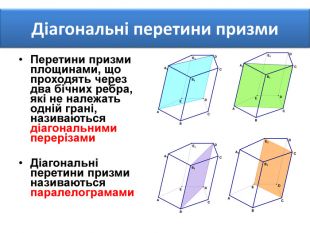
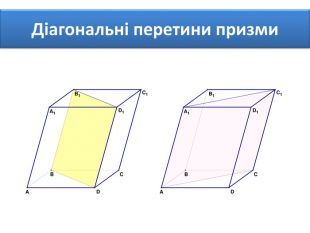
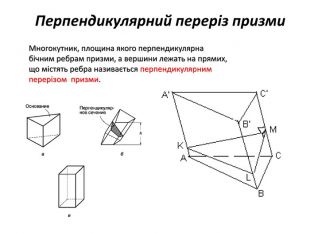
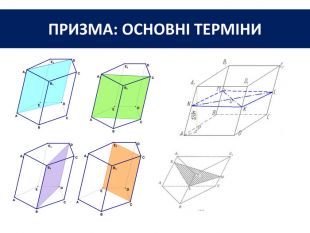
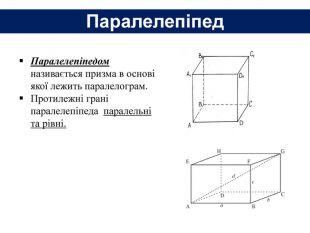
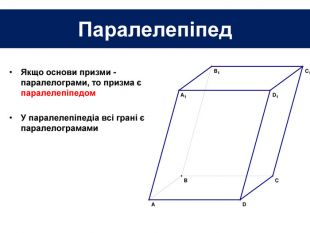
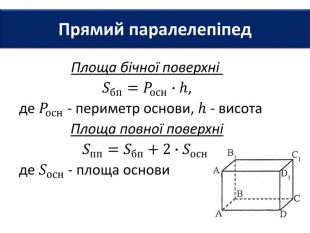
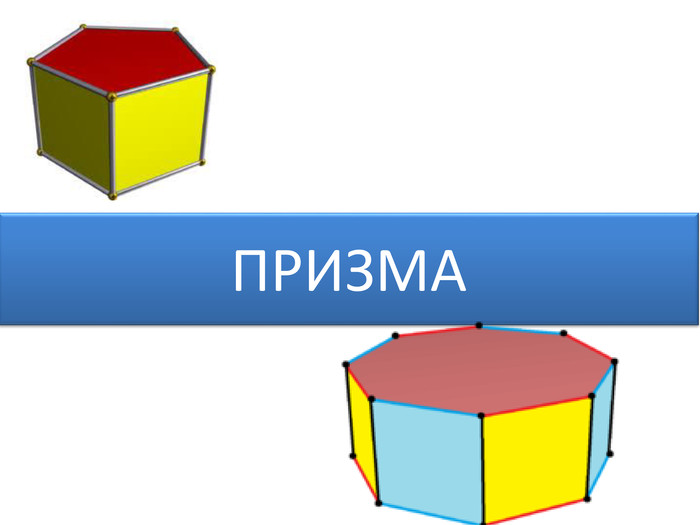
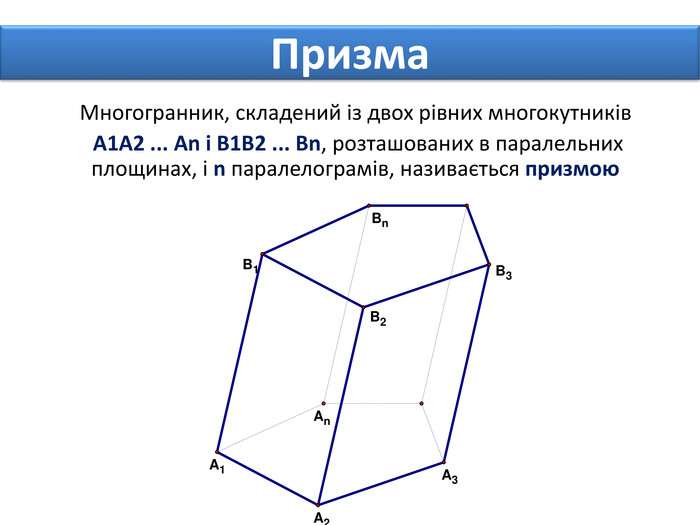
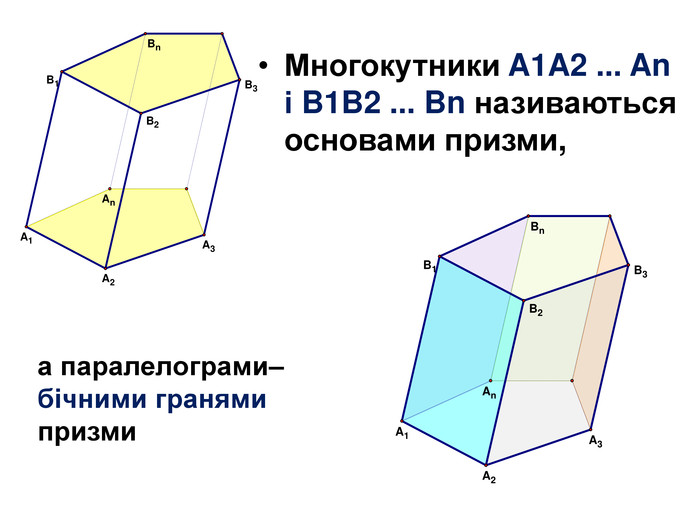
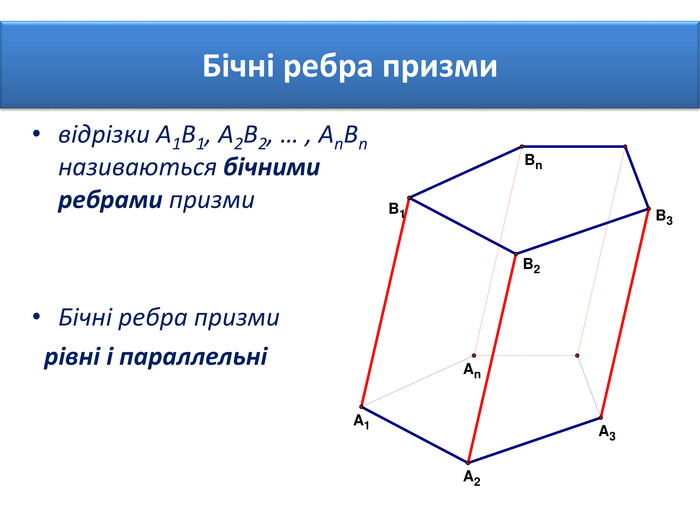
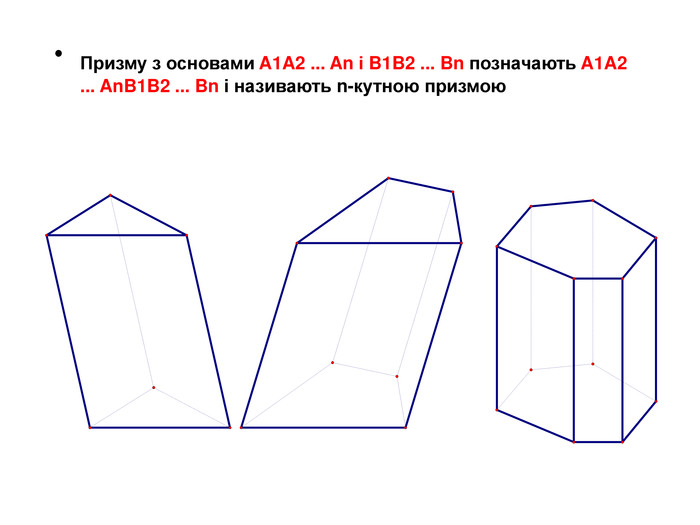
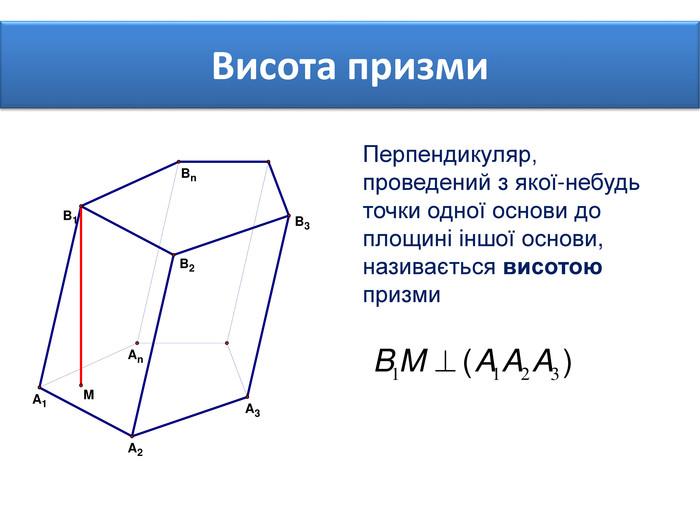
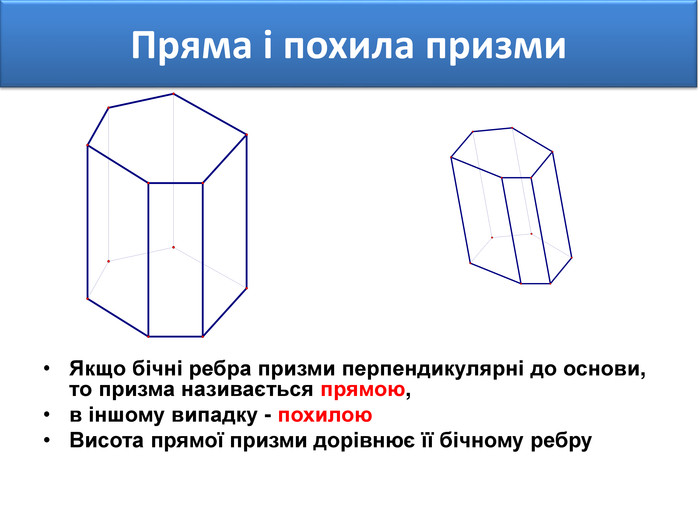
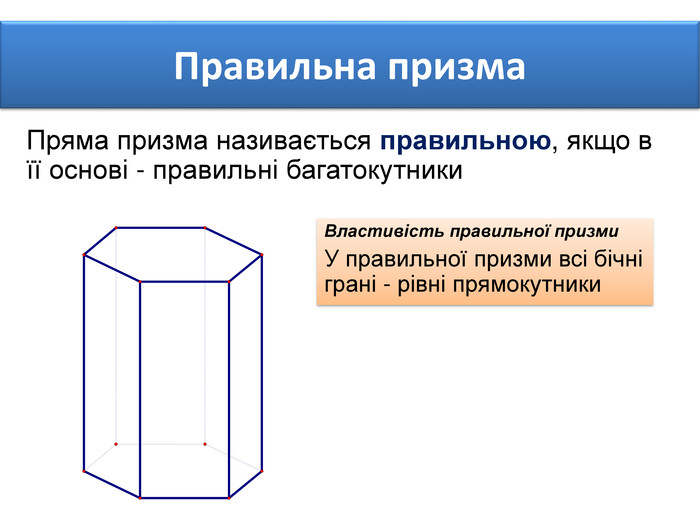
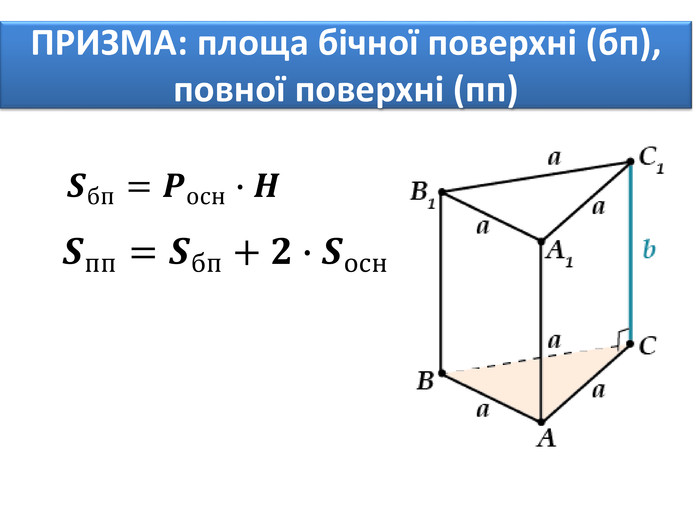
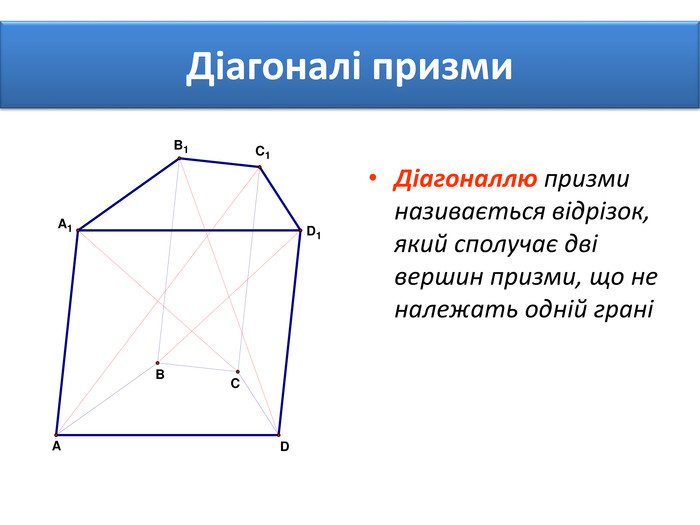
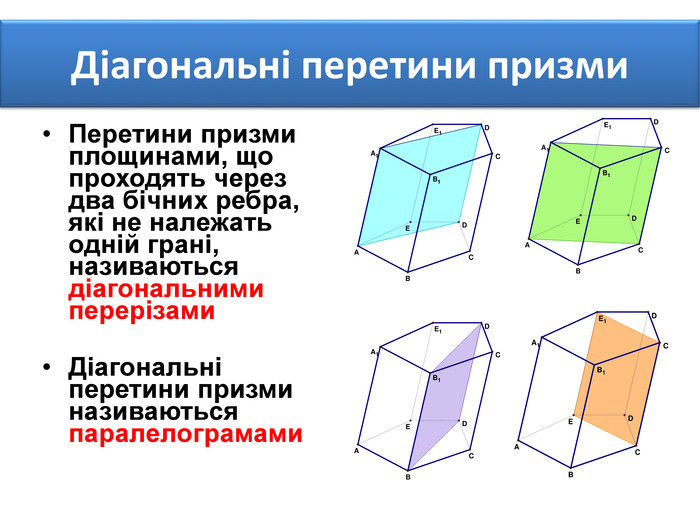
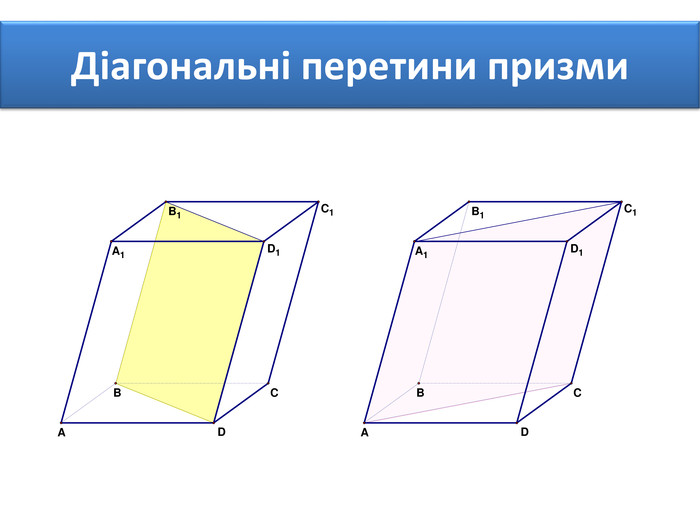
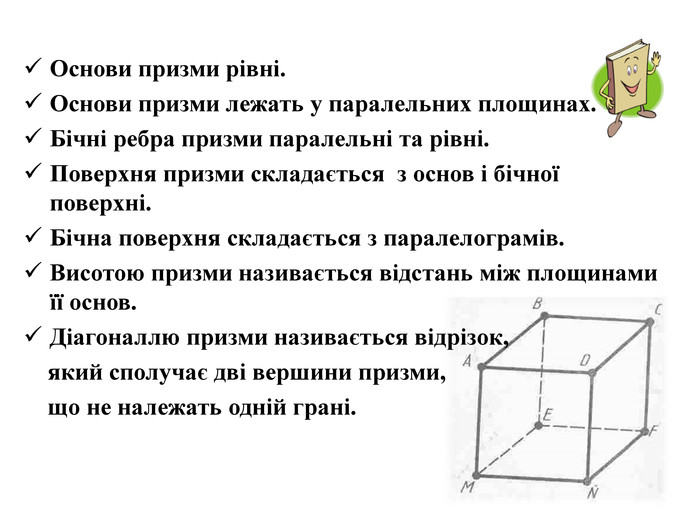
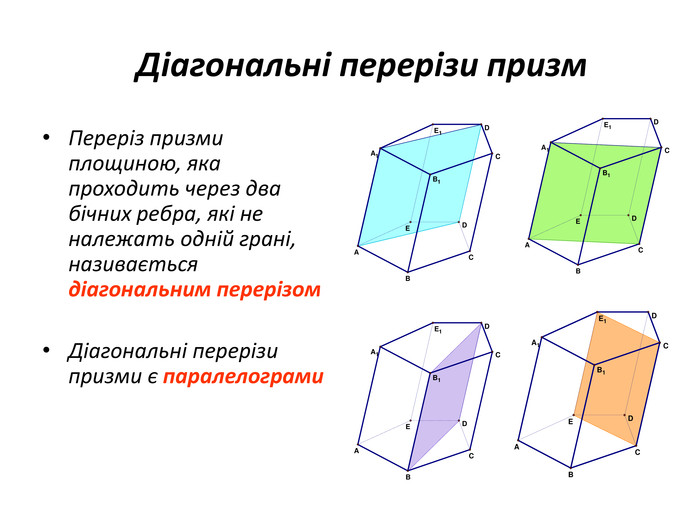
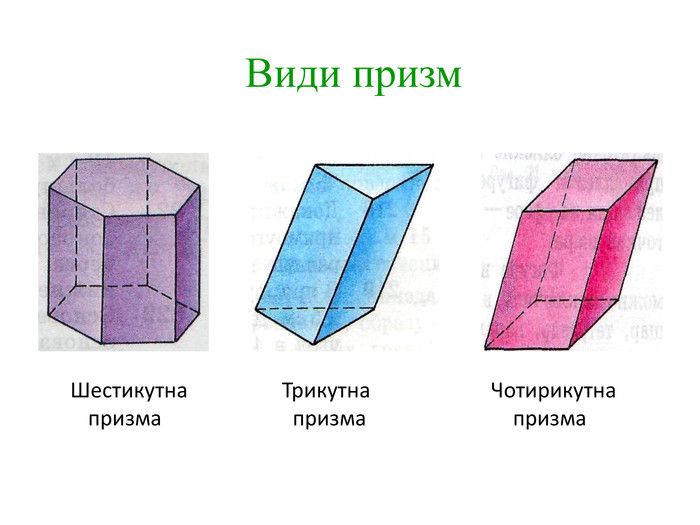
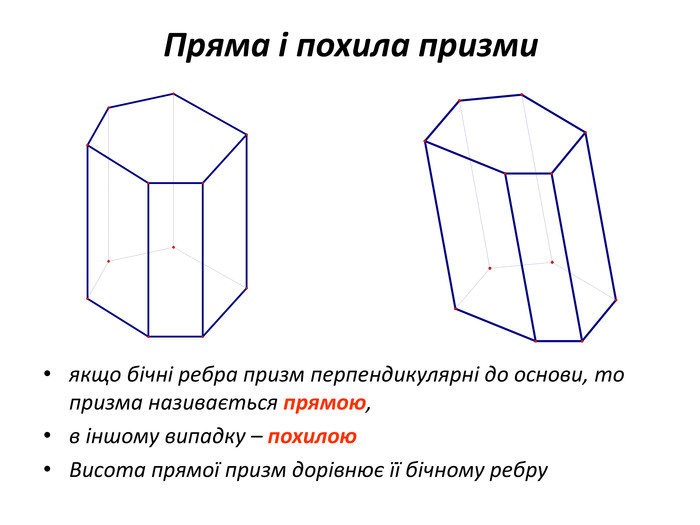
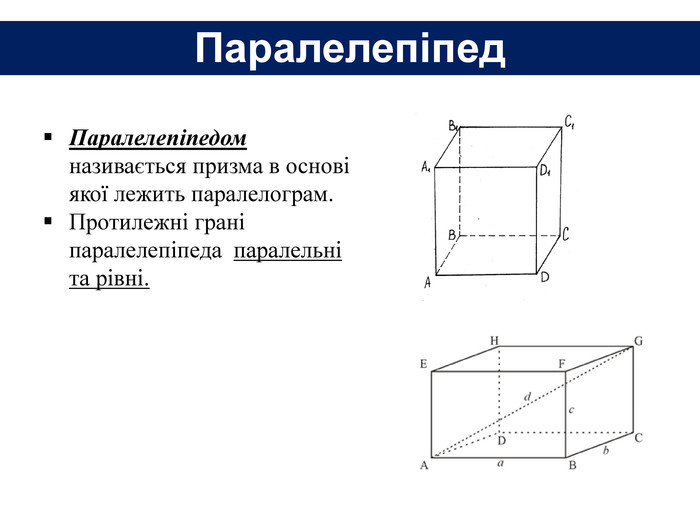
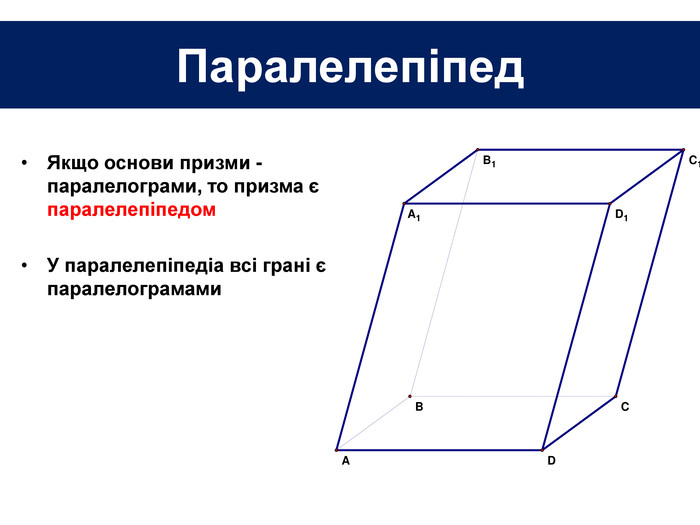
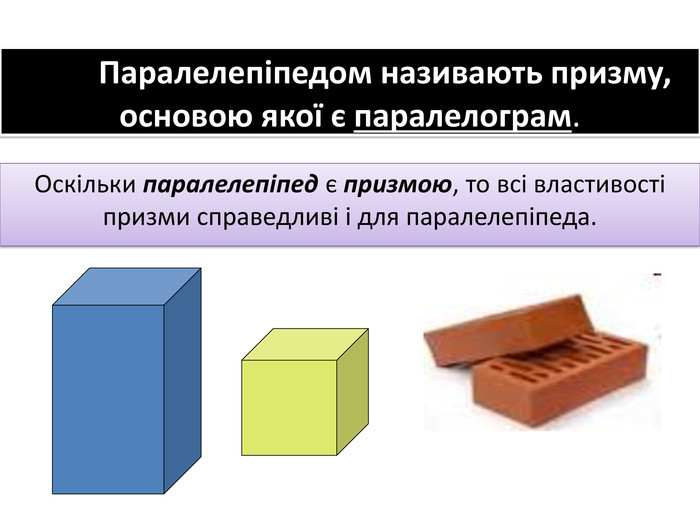
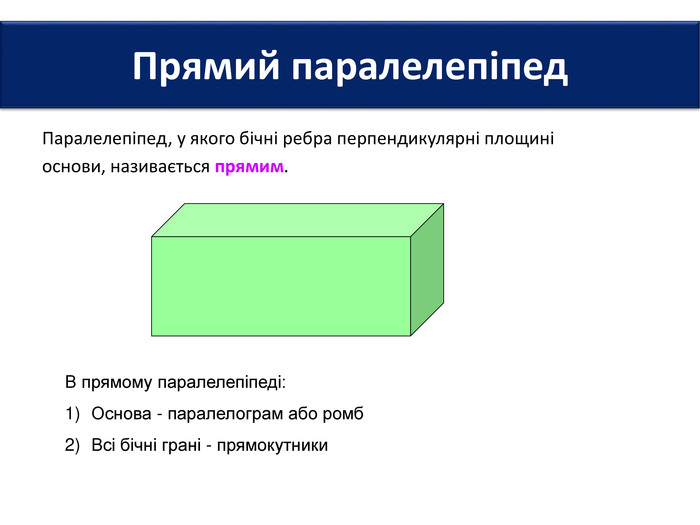
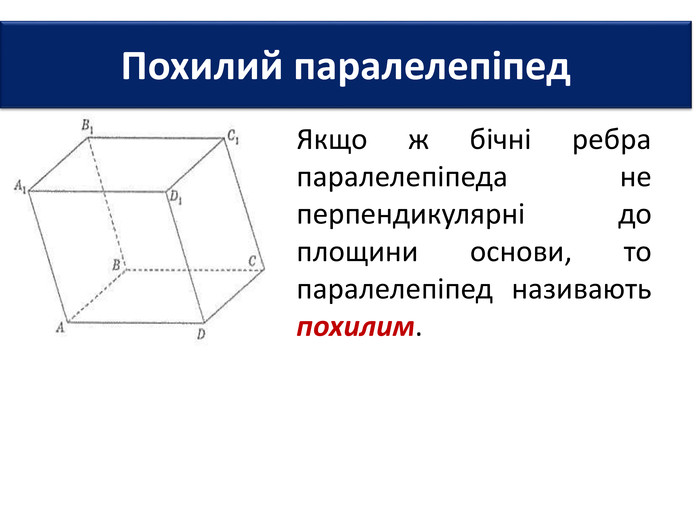
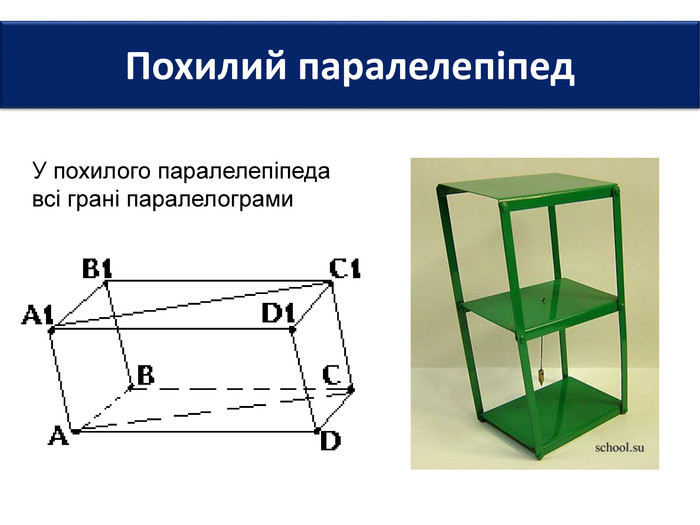
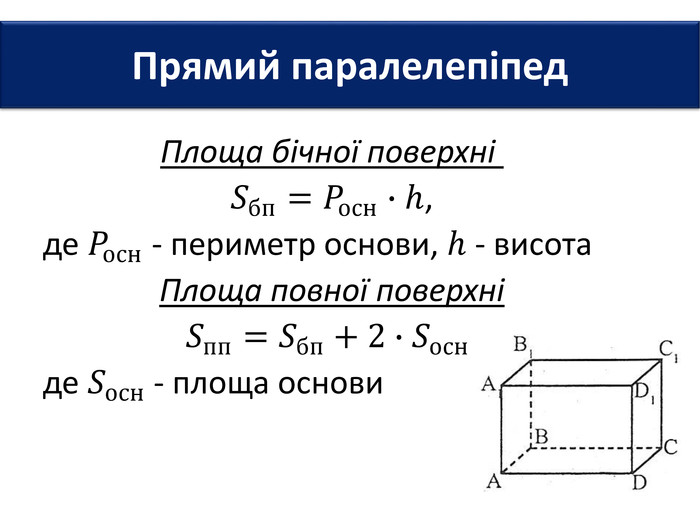
Основи призми рівні. Основи призми лежать у паралельних площинах. Бічні ребра призми паралельні та рівні. Поверхня призми складається з основ і бічної поверхні. Бічна поверхня складається з паралелограмів. Висотою призми називається відстань між площинами її основ. Діагоналлю призми називається відрізок, який сполучає дві вершини призми, що не належать одній грані.

Кількість елементів призми. Кількість: граней n-кутної призми 𝒏+𝟐ребер n-кутної призми 𝟑𝒏вершин n-кутної призми 𝟐𝒏діагоналей n-кутної призми 𝒏−𝟑𝒏сума всіх плоских кутів n-кутної призми 𝟕𝟐𝟎°𝒏−𝟏сума всіх двограних кутів 𝟑𝟔𝟎°𝒏−𝟏 

Діагональні перерізи призм. Переріз призми площиною, яка проходить через два бічних ребра, які не належать одній грані, називається діагональним перерізом. Діагональні перерізи призми є паралелограми

Многокутник, площина якого перпендикулярна бічним ребрам призми, а вершини лежать на прямих, що містять ребра називається перпендикулярним перерізом призми. Перпендикулярний переріз призми

Види призм Шестикутна Трикутна Чотирикутна призма призма призма

Правильні призми

Пряма і похила призмиякщо бічні ребра призм перпендикулярні до основи, то призма називається прямою, в іншому випадку – похилою. Висота прямої призм дорівнює її бічному ребруstyle.colorfillcolorfill.typestyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Задача 1 Знайти площу повної поверхні правильної чотирикутної призми, сторона основи якої дорівнює 5см, а висота – 8см. 

Задача 2 Знайти площу повної поверхні правильної чотирикутної призми, сторона основи якої дорівнює a см, а висота – h см. 

Готуємося до ЗНО

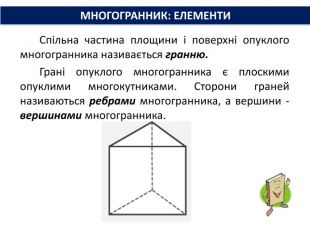
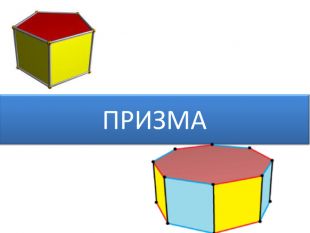
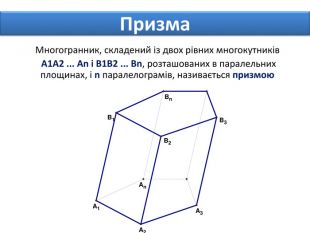
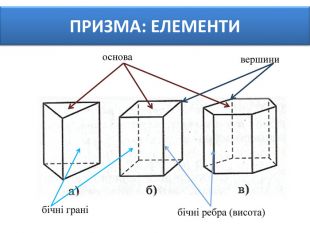
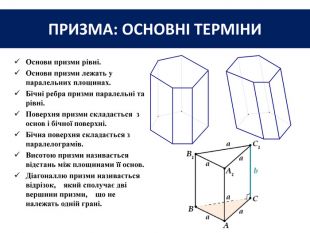
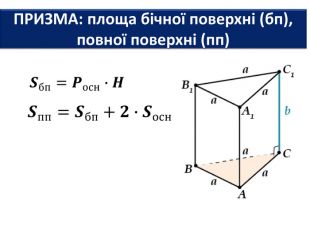
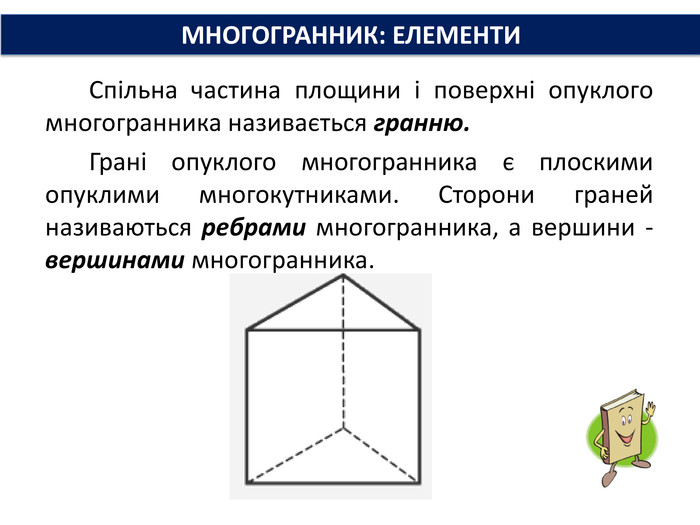
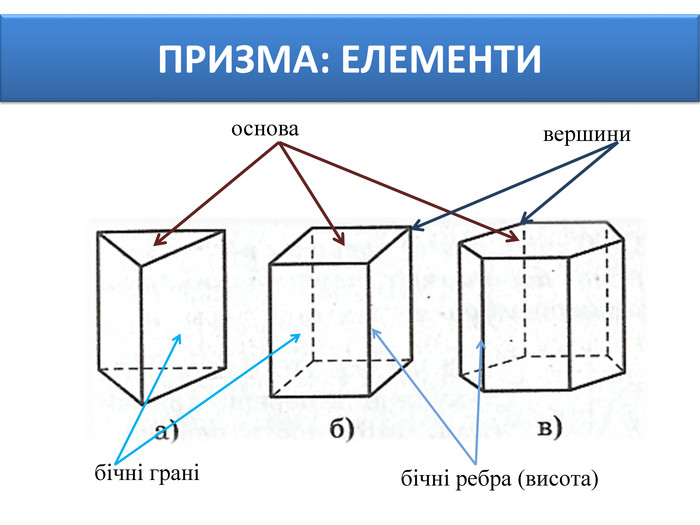
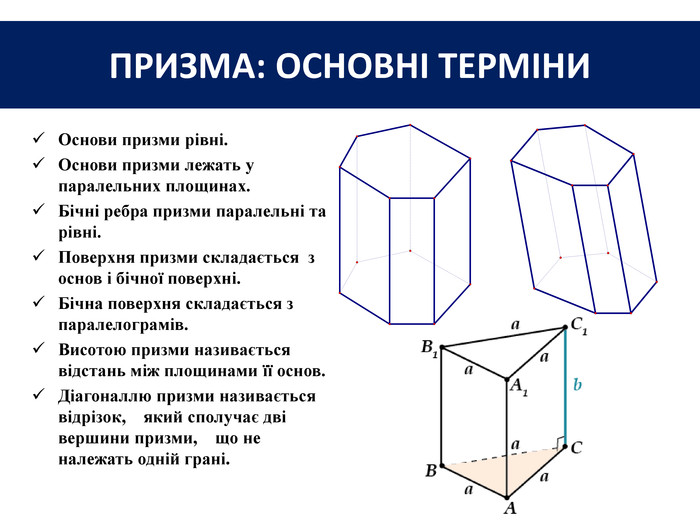
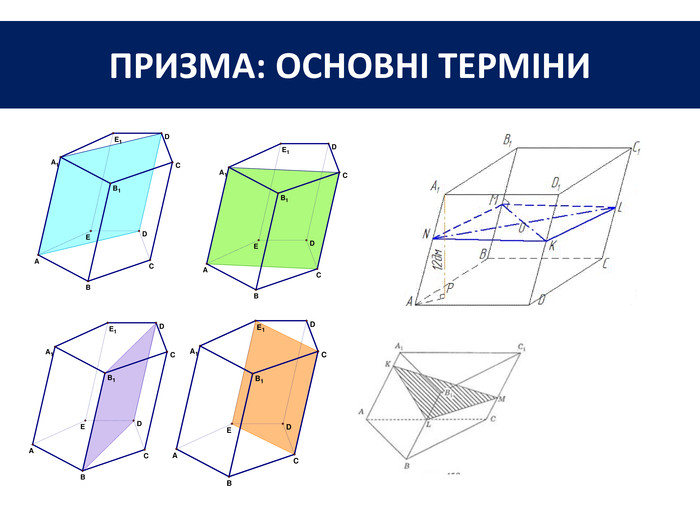
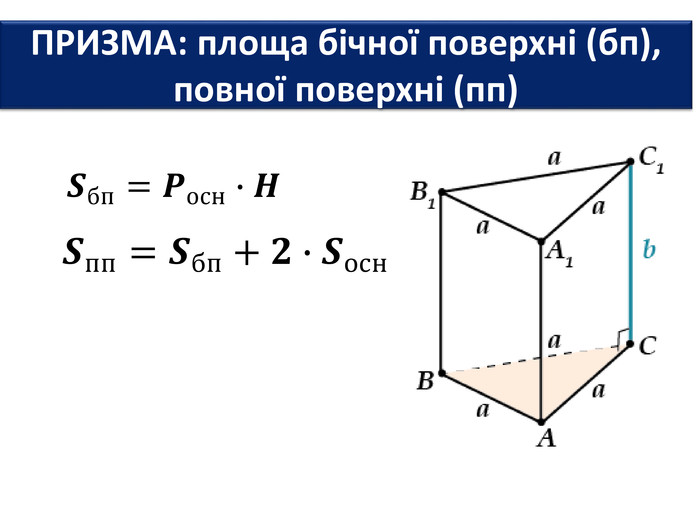
Основи призми рівні. Основи призми лежать у паралельних площинах. Бічні ребра призми паралельні та рівні. Поверхня призми складається з основ і бічної поверхні. Бічна поверхня складається з паралелограмів. Висотою призми називається відстань між площинами її основ. Діагоналлю призми називається відрізок, який сполучає дві вершини призми, що не належать одній грані. ПРИЗМА: ОСНОВНІ ТЕРМІНИ

ПРИЗМА: ОСНОВНІ ТЕРМІНИ

ПРИЗМА: площа бічної поверхні (бп), повної поверхні (пп)𝑺пп=𝑺бп+𝟐∙𝑺осн 𝑺бп=𝑷осн∙𝑯 

Задача. Діагональ правильної чотирикутної призми дорівнює 13 см, а діагональ бічної грані дорівнює 12 см. Знайти площу основи призми. 

Задача. Установити відповідність між сторонами основи та діагоналями (1–4) бічних граней правильних трикутних призм та площами їх бічних поверхонь 

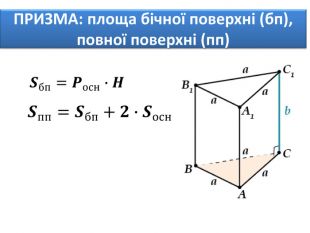
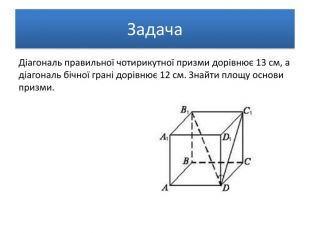
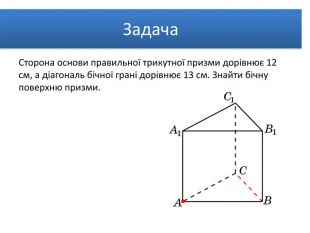
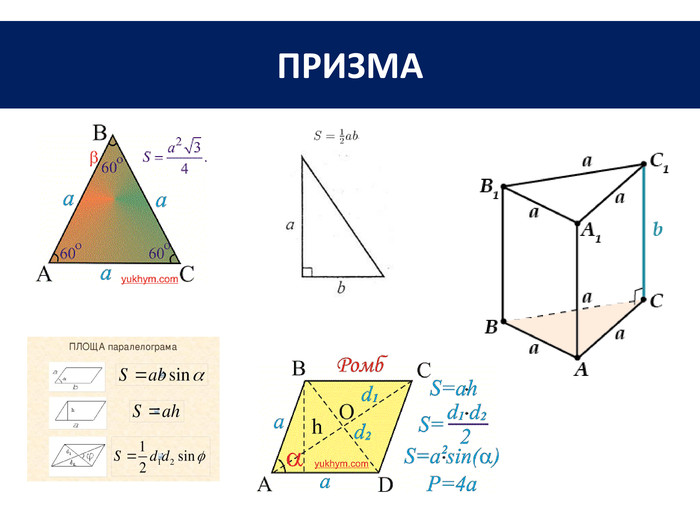
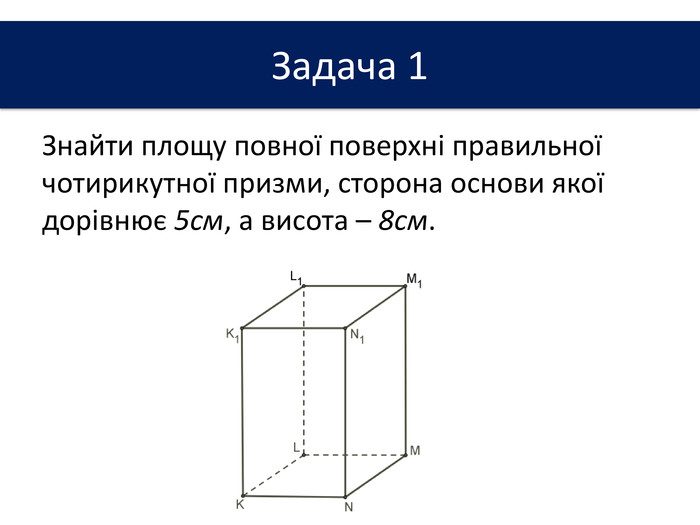
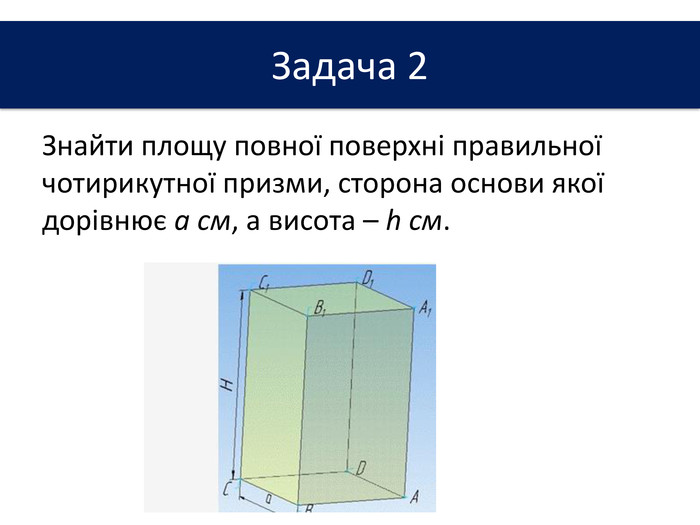
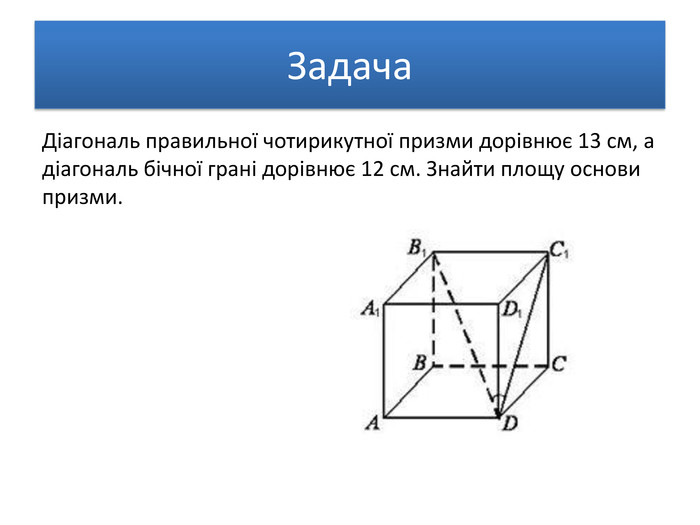
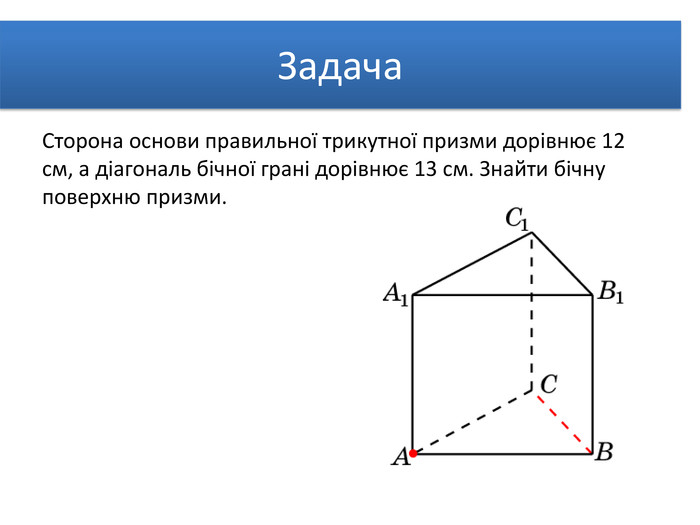
Задача. Бічна поверхня правильної чотирикутної призми дорівнює 64 см2, а повна поверхня – 96 см2. Знайти висоту призми. В основі прямої призми лежить рівнобічна трапеція з основами 4 см і 10 см і бічною стороною 5 см. Бічне ребро призми дорівнює 10 см. Обчислити повну поверхню призми. У правильній чотирикутній призмі площа діагонального перерізу дорівнює S. Визначити площу бічної поверхні.  Задача. Задача

Задача. Сторона основи правильної трикутної призми дорівнює 12 см, а діагональ бічної грані дорівнює 13 см. Знайти бічну поверхню призми. 

Готуємося до ЗНО

Готуємося до ЗНО

Паралелепіпедом називається призма в основі якої лежить паралелограм. Протилежні грані паралелепіпеда паралельні та рівні. Паралелепіпед

Паралелепіпед. Якщо основи призми - паралелограми, то призма є паралелепіпедом У паралелепіпедіа всі грані є паралелограмамиstyle.colorfillcolorfill.typestyle.colorfillcolorfill.type

Діагоналі паралелепіпеда перетинаються в одній точці і точкою перетину діляться навпіл У прямокутному паралелепіпеді квадрат будь-якої діагоналі дорівнює сумі квадратів трьох його вимірів Паралелепіпед

Діагоналі паралелепіпеда. Діагоналі паралелепіпеда перетинаються в одній точці і діляться цією точкою навпілstyle.colorfillcolorfill.type

Паралелепіпедом називають призму, основою якої є паралелограм. Оскільки паралелепіпед є призмою, то всі властивості призми справедливі і для паралелепіпеда.

Прямий паралелепіпед. Паралелепіпед, у якого бічні ребра перпендикулярні площиніоснови, називається прямим. В прямому паралелепіпеді: Основа - паралелограм або ромб. Всі бічні грані - прямокутники

Якщо ж бічні ребра паралелепіпеда не перпендикулярні до площини основи, то паралелепіпед називають похилим. Похилий паралелепіпед

Похилий паралелепіпед. У похилого паралелепіпеда всі грані паралелограми

Куб (гексаедр) —правильний багатогранник, кожна грань якого є квадратом. Окремий випадок паралелепіпеда і призми. Куб

Куб. Прямокутний паралелепіпед, у якого всіребра рівні, називається кубом. У куба всі грані - квадрати. Квадрат діагоналі куба дорівнює потроєному квадрату його виміру.

Куб. Площа бічної поверхні S бп = 4a , де а - ребро куба. Площа повної поверхніS пп = 6a

Куб. Задача. Діагональ куба дорівнює 6 см. Знайдіть площу повної поверхні куба. 

Прямокутний паралелепіпед. Прямий паралелепіпед, у якого основою є прямокутник, називається прямокутним паралелепіпедом. Усі грані прямокутного паралелепіпеда – прямокутники. У прямокутному паралелепіпеді квадрат будь - якої діагоналі дорівнює сумі квадратів трьох його вимірів.

Прямий паралелепіпед. Площа бічної поверхні 𝑆бп=𝑃осн∙h, де 𝑃осн - периметр основи, h - висота. Площа повної поверхні𝑆пп=𝑆бп+2∙𝑆осн де 𝑆осн - площа основи 

Прямокутний паралелепіпед. Площа бічної поверхні S бп = 2c (a + b), де a, b - сторони основи, c - бічне ребро прямокутного паралелепіпеда. Площа повної поверхні S пп = 2 (ab + bc + ac)

Задачі1. Діагональ куба дорівнює 9 см. Знайти ребро куба.2. В прямокутному паралелепіпеді лінійні виміри дорівнюють 2 см, 3 см, 4 см. Знайти квадрат діагоналі

Задача Обчислити діагоналі прямокутного паралелепіпеда за трьома його вимірами: 7 см, 2 см і 12 см.

Сторона основи прямокутного паралелепіпеда дорівнюють a і b. Діагональ паралелепіпеда нахилена до площини основи під кутом 𝛽 . Визначити висоту паралелепіпеда. Задача

4. Знайти діагональ прямокутного паралелепіпеда, виміри якого дорівнюють 2 см, 3 см і 6 см. Задачі5. Сторони основи прямокутного паралелепіпеда дорівнюють 5 см і 12 см, а діагональ паралелепіпеда нахилена до площини основи під кутом 450. Знайти бічне ребро паралелепіпеда.

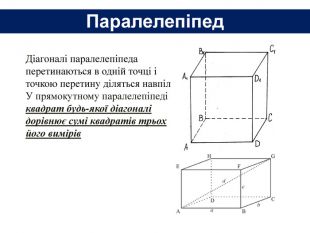
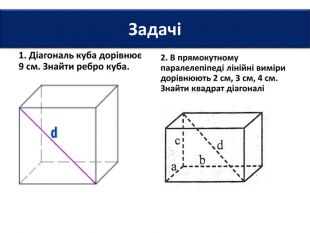
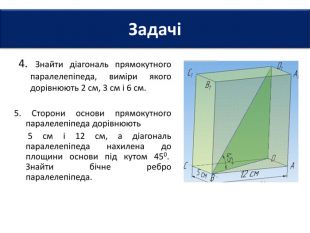
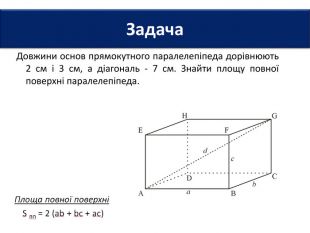
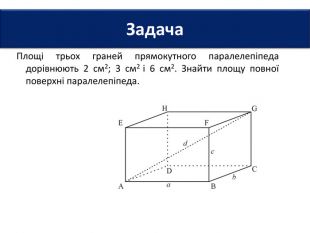
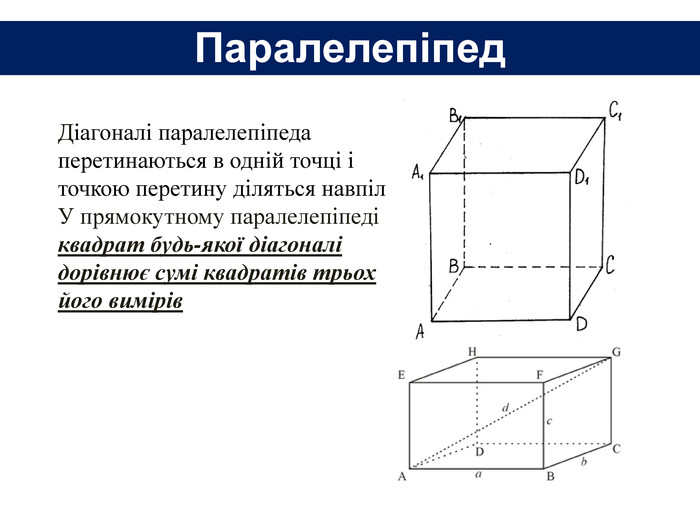
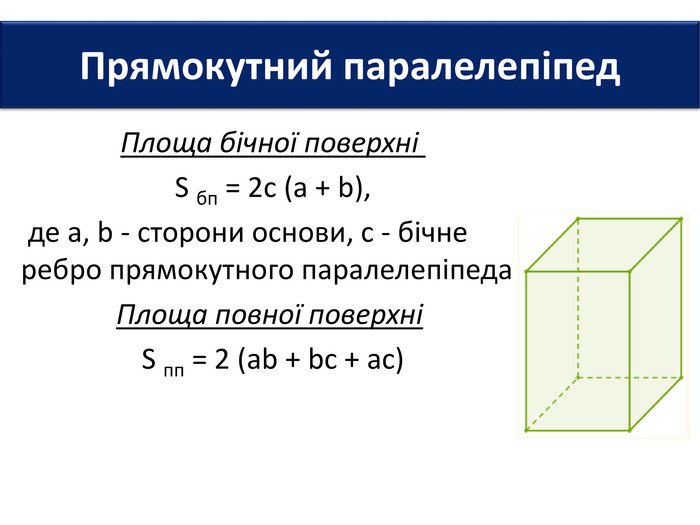
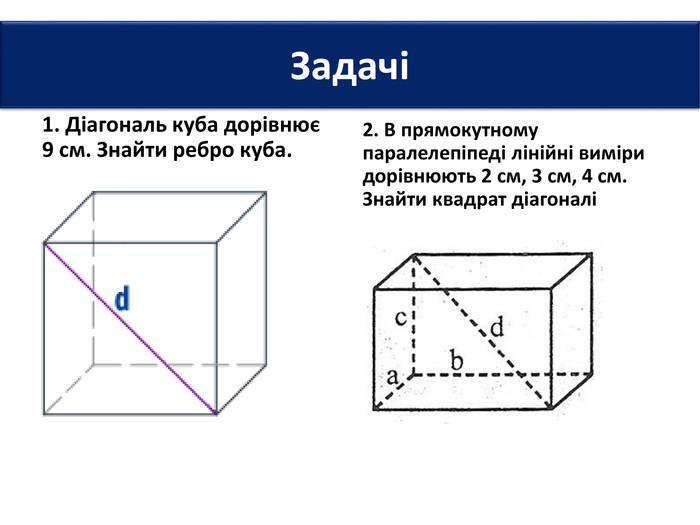
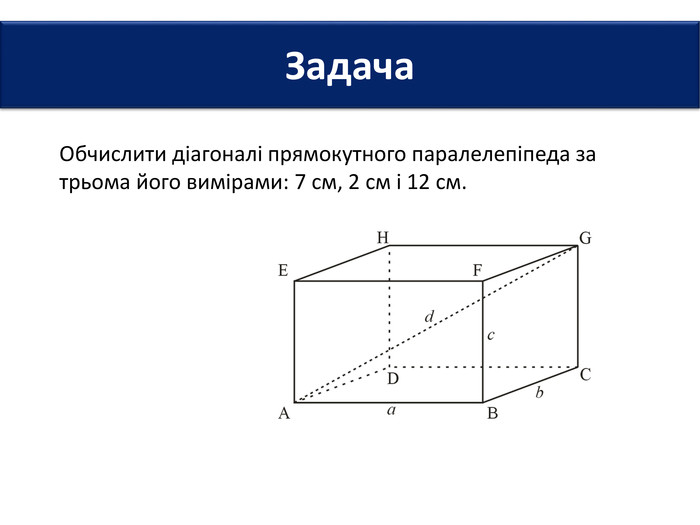
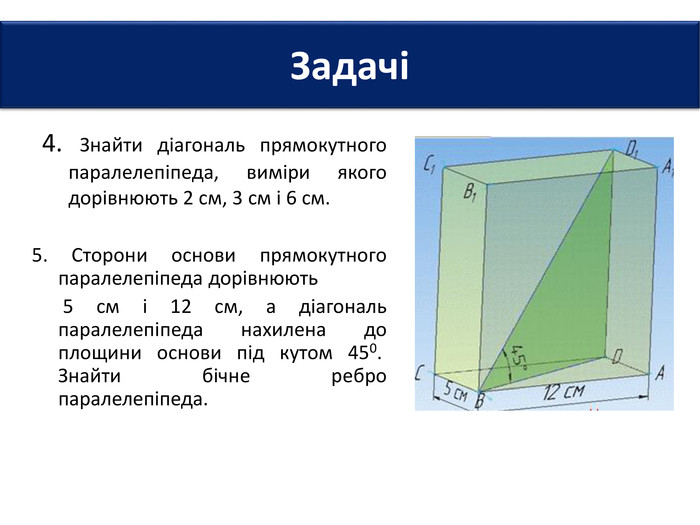
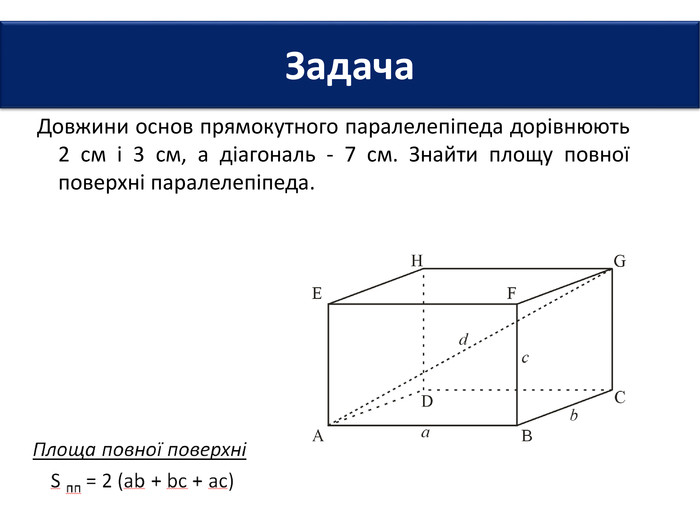
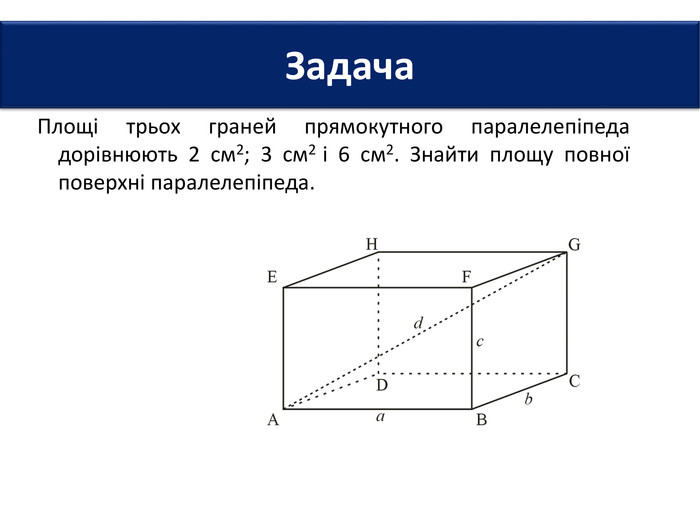
6. Довжини основ прямокутного паралелепіпеда дорівнюють 2 см і 3 см, а діагональ - 7 см. Знайти площу повної поверхні паралелепіпеда.7. Площі трьох граней прямокутного паралелепіпеда дорівнюють 2 см2; 3 см2 і 6 см2. Знайти площу повної поверхні паралелепіпеда.8. Сторони основи прямокутного паралелепіпеда дорівнюють 6 см і 8 см, а висота - 3 см. Знайти площу діагонального перерізу паралелепіпеда. Задачі

 9. Знайти площу (у см2) повної поверхні прямокутного паралелепіпеда, якщо його діагональ більша за лінійні виміри відповідно на 2 см, 5 см і 9 см. Задачі

Довжини основ прямокутного паралелепіпеда дорівнюють 2 см і 3 см, а діагональ - 7 см. Знайти площу повної поверхні паралелепіпеда. Задача

Площі трьох граней прямокутного паралелепіпеда дорівнюють 2 см2; 3 см2 і 6 см2. Знайти площу повної поверхні паралелепіпеда. Задача

Задача 10 В основі прямокутного паралелепіпеда лежить квадрат. Знайти висоту паралелепіпеда, якщо площа його повної поверхні дорівнює 160 см2, а площа бічної поверхні – 128 см2.

Готуємося до ЗНО