Презентація до уроку алгебри в 10 класі "Показникові рівняння.Способи розв'язування показникових рівнянь "

Показникові рівняння. Показниковими називаються рівняння,у яких невідоме міститься в показнику степеня при постійних основах. Наприклад:  2𝑥 +3=0; 3𝑥+1−3𝑥−1=0; 5𝑥=125. 

Розв'яжіть рівняння. Приклад 1.      𝟓𝒙=𝟏𝟐𝟓 Розв'язання. Оскільки      𝟓𝒙=𝟏𝟐𝟓, а 𝟏𝟐𝟓=𝟓𝟑, то маємо       𝟓𝒙=𝟓𝟑, звідси 𝒙=𝟑 Відповідь: 3 

Приклад 2. Розв'яжіть рівняння 𝟏𝟕𝒙=𝟒𝟗. Розв'язання. Оскільки 𝟒𝟗=𝟕𝟐=𝟏𝟕−𝟐,то 𝟏𝟕х=𝟏𝟕−𝟐, звідси 𝒙=−𝟐. Відповідь : -2 

Приклад 3. Розв'яжіть рівняння 𝟏𝟓𝒙𝟐−𝟓𝒙+𝟔=𝟏. Розв'язання. Оскільки 1=𝟏𝟓𝟎,то 𝟏𝟓𝒙𝟐−𝟓𝒙+𝟔=𝟏𝟓𝟎, 𝒙𝟐−𝟓𝒙+𝟔= 0, звідси 𝒙𝟏=𝟐 ,𝒙𝟐=𝟑. Відповідь : 2; 3 

Приклад 4.      𝟐𝒙−𝟐=−𝟐. Розв'язання. Оскільки      𝟐𝒙−𝟐>𝟎 при всіх 𝒙, то рівняння коренів немає. Відповідь: коренів немає 

Способи розв'язування показникових рівнянь. Спосіб зведення до спільної основи. Приклад . Розв'яжіть рівняння 𝟐𝒙∙𝟓𝒙=𝟎,𝟏𝟏𝟎𝒙−𝟏𝟑 Розв'язання.𝟐𝒙∙𝟓𝒙=𝟎,𝟏𝟏𝟎𝒙−𝟏𝟑𝟏𝟎𝒙=𝟏𝟎−𝟏∙𝟏𝟎𝟑𝒙−𝟑𝟏𝟎𝒙=𝟏𝟎𝟑𝒙−𝟒𝒙=𝟑𝒙−𝟒𝒙=𝟐 Відповідь:2 

2. Спосіб винесення спільного множника за дужки. Приклад1. Розв'яжіть рівняння 𝟑𝒙−𝟐∙𝟑𝒙−𝟐=𝟔𝟑 Розв'язання. 𝟑𝒙−𝟐∙𝟑𝒙−𝟐=𝟔𝟑𝟑𝒙−𝟐𝟑𝟐−𝟐 =63𝟑𝒙−𝟐∙𝟕 =63𝟑𝒙−𝟐=𝟗𝒙−𝟐=𝟐𝒙=𝟒 Відповідь:4 

Приклад 2. Розв'яжіть рівняння 𝟓𝟐𝒙−𝟏−𝟓𝟐𝒙+𝟐𝟐𝒙+𝟐𝟐𝒙+𝟐=𝟎 Розв'язання. 𝟐𝟐𝒙+𝟐𝟐𝒙+𝟐= 𝟓𝟐𝒙−𝟓𝟐𝒙−𝟏𝟐𝟐𝒙(𝟏+𝟐𝟐)= 𝟓𝟐𝒙(𝟏−𝟓−𝟏)𝟐𝟐𝒙∙𝟓=𝟓𝟐𝒙∙𝟒𝟓 поділимо на 𝟓𝟐𝒙∙ 𝟓𝟐𝟐𝒙𝟓𝟐𝒙=𝟒𝟐𝟓;       𝟐𝟓𝟐𝒙=𝟐𝟓𝟐; 𝟐𝒙=𝟐 ;       𝒙=𝟏 Відповідь: 1 

3. Спосіб зведення рівняння до квадратного. Приклад1. Розв'яжіть рівняння 𝟒𝟗𝒙−𝟖∙𝟕𝒙+𝟕=𝟎. Розв'язання.𝟒𝟗𝒙−𝟖∙𝟕𝒙+𝟕=𝟎𝟕𝟐𝒙−𝟖∙𝟕𝒙+𝟕=𝟎𝟕𝒙𝟐−𝟖∙𝟕𝒙+𝟕=𝟎 Заміна: 𝟕𝒙=𝒕 , тоді 𝒕𝟐−𝟖∙𝒕+𝟕=𝟎 , звідси 𝒕𝟏=𝟕;  𝒕𝟐=𝟏 З урахуванням заміни 𝟕𝒙=𝒕 ,  маємо: 𝒕𝟏=𝟕 , 𝟕𝒙=𝟕 ;𝒙=𝟏;𝒕𝟐=𝟏, 𝟕𝒙=𝟏 ;       𝟕𝒙=𝟕𝟎,     𝒙=𝟎. Відповідь: 1; 0.  

Приклад 2. 𝟑∙𝟏𝟔𝒙+𝟐∙𝟖𝟏𝒙=𝟓∙𝟑𝟔𝒙. Розв'язування.𝟑∙𝟒𝟐𝒙+𝟐∙𝟗𝟐𝒙=𝟓∙𝟒𝒙∙𝟗𝒙𝟑∙𝟒𝟐𝒙𝟗𝟐𝒙+𝟐∙𝟗𝟐𝒙𝟗𝟐𝒙=𝟓∙𝟒𝒙∙𝟗𝒙𝟗𝟐𝒙𝟑∙𝟒𝟗𝟐𝒙−𝟓∙𝟒𝟗𝒙+𝟐=𝟎 Заміна:𝟒𝟗𝒙=t , тоді 𝟑∙𝒕𝟐−𝟓∙𝒕+𝟐=𝟎, звідси 𝒕𝟏=𝟐𝟑 ;𝒕𝟐=𝟏 З урахуванням заміни,маємо:𝟏)𝒕𝟏=𝟐𝟑    𝟒𝟗𝒙=𝟐𝟑 𝟐𝟑𝟐𝒙=𝟐𝟑 𝟐𝒙=𝟏    ; 𝒙=𝟏𝟐2) 𝒕𝟐=𝟏     𝟒𝟗𝒙=1 𝒙=𝟎 Відповідь:0;1 

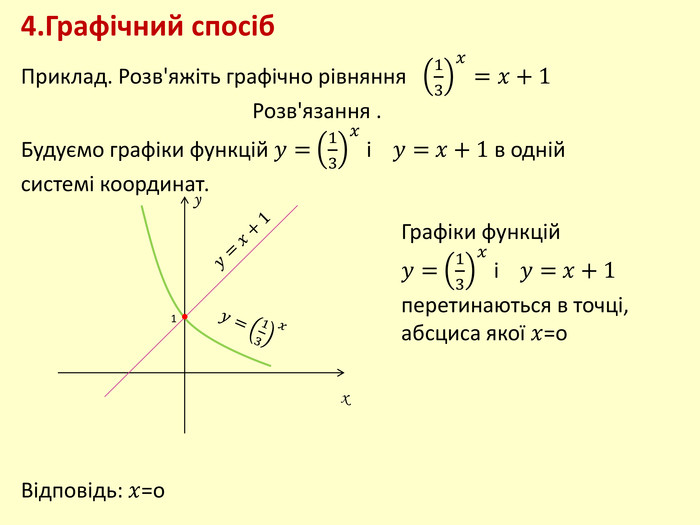
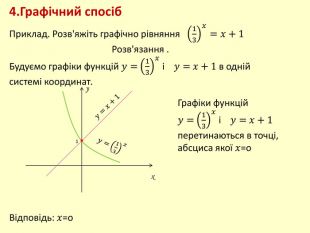
4. Графічний спосіб. Приклад. Розв'яжіть графічно рівняння 13𝑥=𝑥+1 Розв'язання . Будуємо графіки функцій 𝑦= 13𝑥 і 𝑦= 𝑥+1 в одній системі координат. 1ху𝑦= 𝑥+1  𝑦= 13𝑥 Графіки функцій 𝑦= 13𝑥 і 𝑦= 𝑥+1 перетинаються в точці, абсциса якої 𝑥=о Відповідь: 𝑥=о