Презентація до уроку алгебри в 9 класі "Побудова графіка квадратичної функції"
Про матеріал
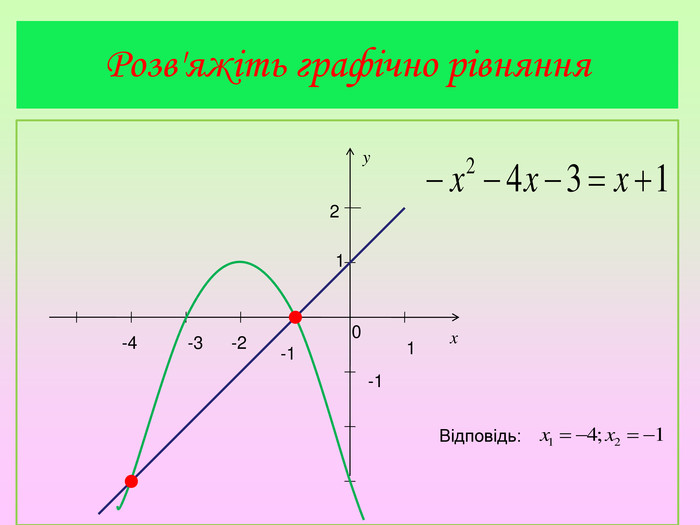
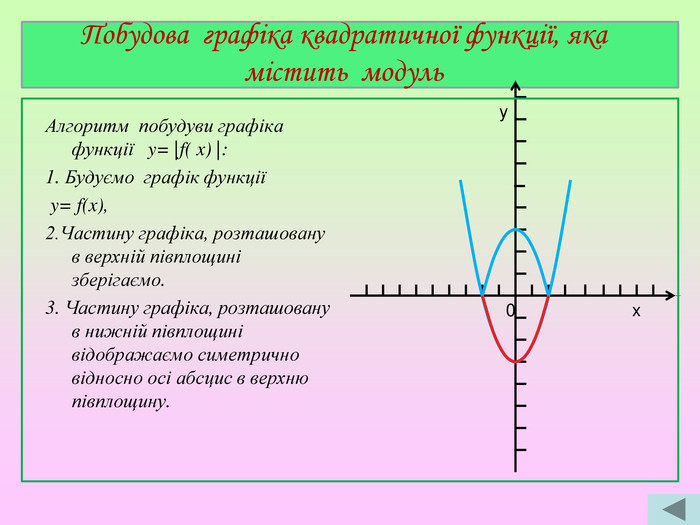
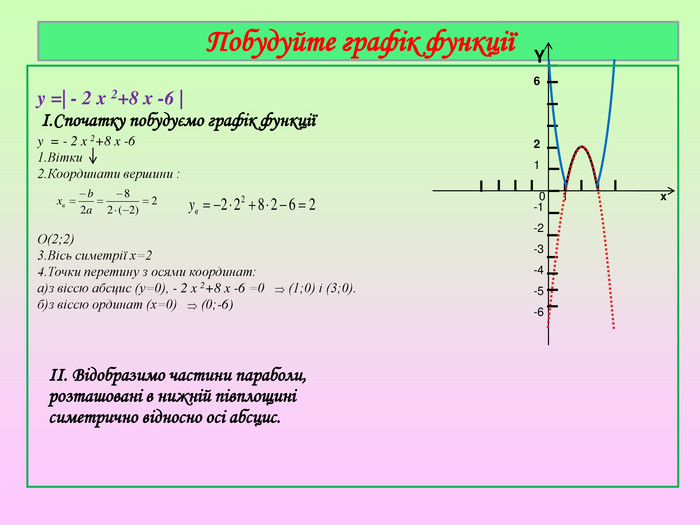
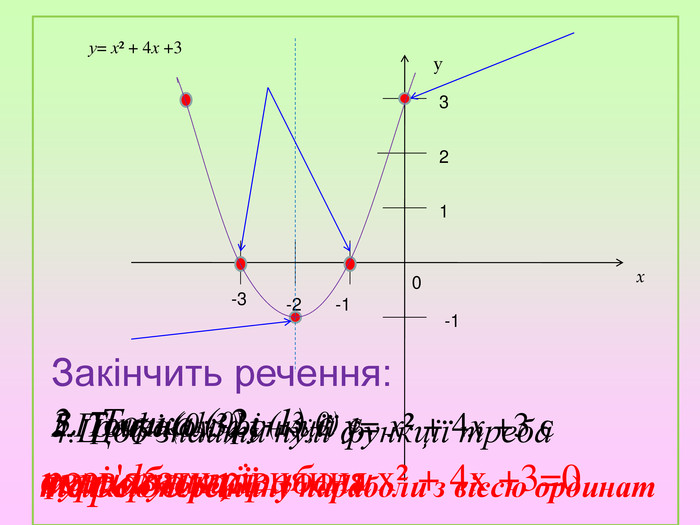
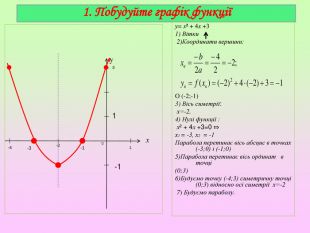
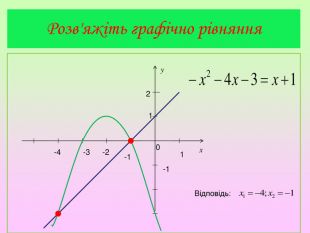
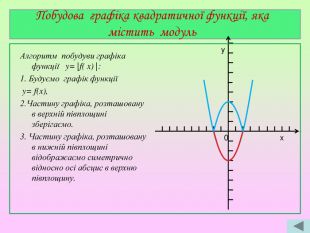
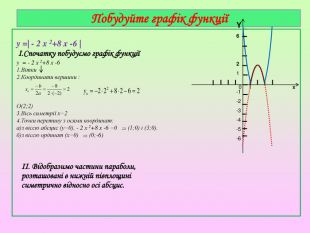
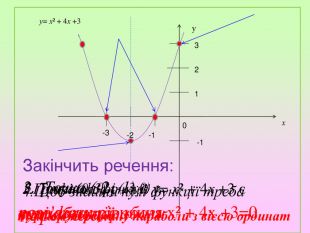
Презентація містять завдання актуалізації опорних знань, побудову графіка квадратичної функції, графічне розв'язування рівнянь.. Побудова графіка є поетапною та наглядною.
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 9 клас (Бевз Г.П., Бевз В.Г.)
До уроку
Розділ 2. КВАДРАТИЧНА ФУНКЦІЯ Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку




























-

Приходько Наталія Михайлівна
14.12.2023 в 21:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Олішкевич Валентина Петрівна
08.12.2018 в 13:17
Дякую!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Посохова Людмила Вікторівна
25.02.2018 в 21:25
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Туінов Іван Володимирович
21.02.2018 в 19:33
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Туінова Світлана Григоріївна
21.02.2018 в 19:25
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Туінова Тетяна Іванівна
21.02.2018 в 19:19
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 3 відгука