Презентація до уроку геометрії в 9 класі з теми "Правильні многокутники"

Правильні многокутники

В світі немає місця для некрасивої математики Г.Х.Харді

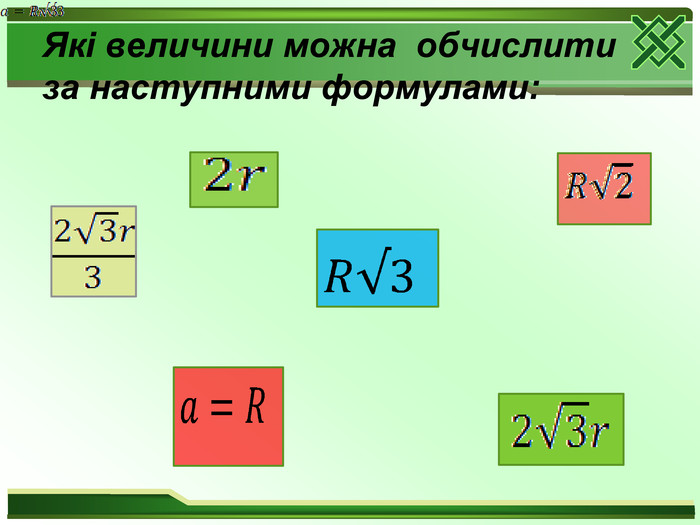
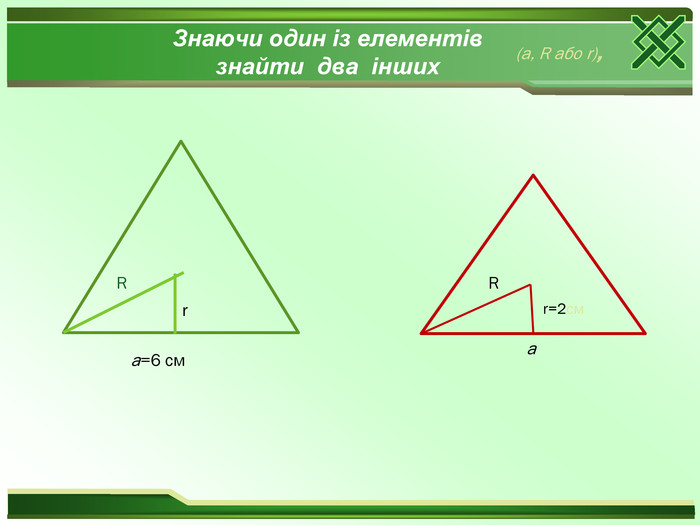
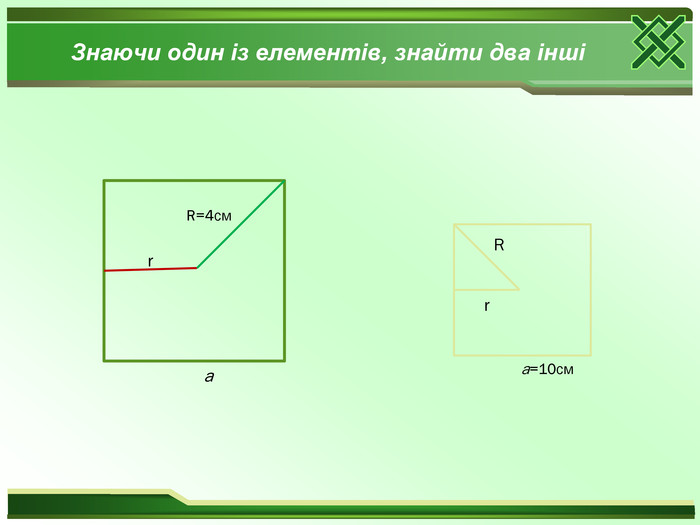
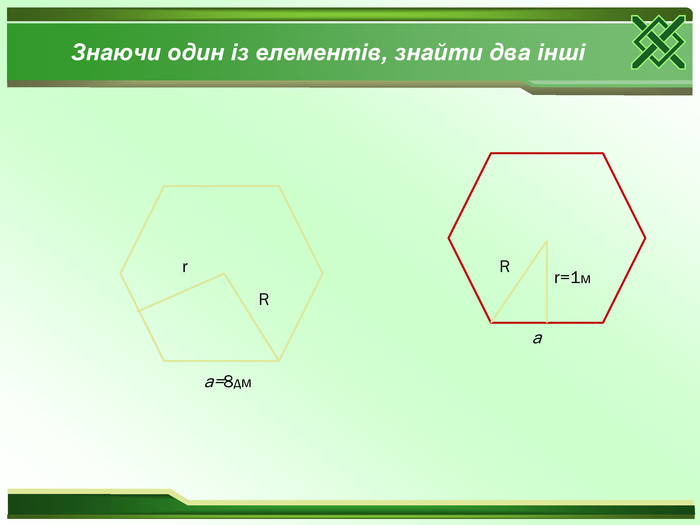
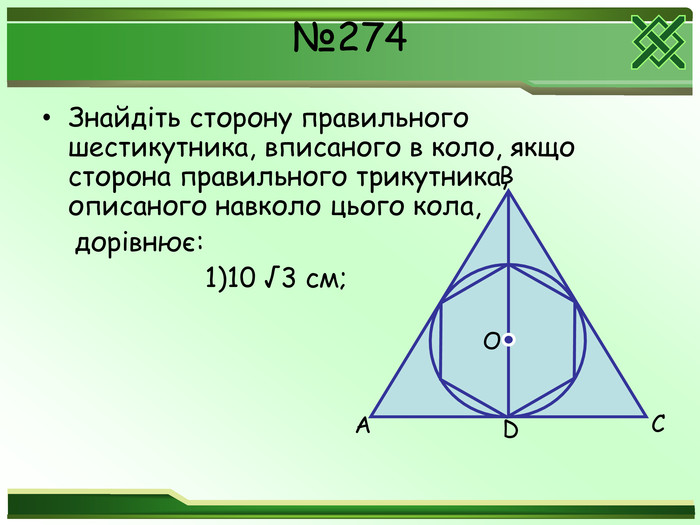
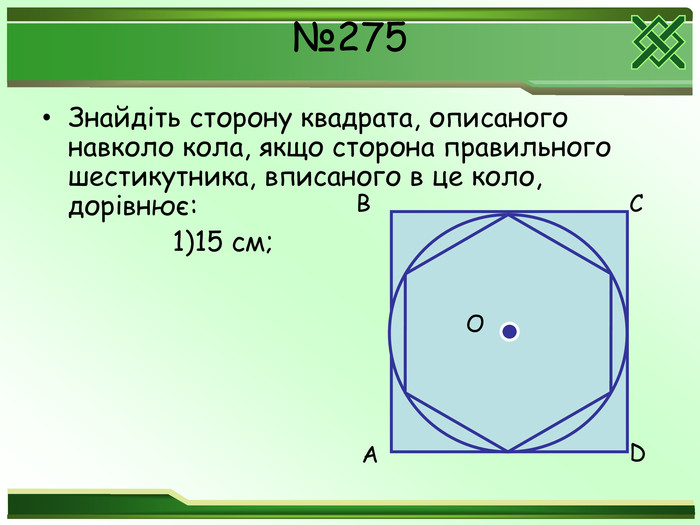
Який многокутник називається правильним? Яке найменше число можна поставити замість «много»? Чи вірно , що будь-який рівносторонній трикутник являється правильним? Чи вірно, що будь-який рівносторонній чотирикутник являється правильним? Знайдіть величину внутрішнього кута при будь – якій вершині правильного :  а)трикутника; б)чотирикутника; в)шестикутника. Знайдіть величину зовнішнього кута при будь – якій вершині правильного :  а)трикутника; б)чотирикутника; в)шестикутника. Що називається центром правильного многокутника?

Які величини можна обчислити за наступними формулами:

Знаючи один із елементів знайти два інших R r a=6 см r=2см R a (a, R або r),

Знаючи один із елементів, знайти два інші r R=4см а а=10см R r

Знаючи один із елементів, знайти два інші а=8дм R r r=1м R а

№260 а- сторона правильного трикутника, Р – його периметр, R I r – радіуса описаного і вписаного кіл. Накресліть у зошиті таблицю та заповніть її

№264 а- сторона правильного чотирикутника, Р – його периметр, R I r – радіуса описаного і вписаного кіл. Накресліть у зошиті таблицю та заповніть її

№268 а- сторона правильного шестикутника, Р – його периметр, R I r – радіуса описаного і вписаного кіл. Накресліть у зошиті таблицю та заповніть її

№274 Знайдіть сторону правильного шестикутника, вписаного в коло, якщо сторона правильного трикутника, описаного навколо цього кола, дорівнює: 1)10 √3 см; А В С D O

№275 Знайдіть сторону квадрата, описаного навколо кола, якщо сторона правильного шестикутника, вписаного в це коло, дорівнює: 1)15 см; А В С D O

Сума кутів, що сходяться в одній вершині, дорівнює 360˚  (60˚·6=360˚; 90˚ ·4=360˚; 120˚·3=360˚). 

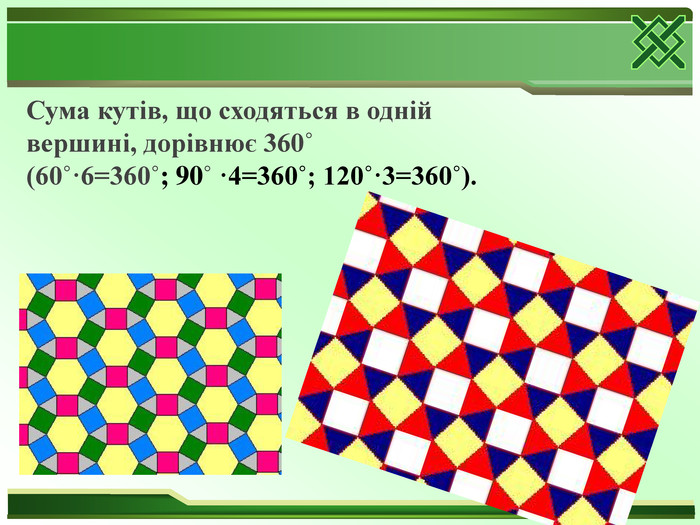
Чи знають бджоли математику ? Учені, які досліджували бджолині стільники, переконалися: всі кути, що утворюють шестикутник бджолиної чарунки саме такі, для яких чарунка найбільш містка і при цьому на неї йде найменше воску. Начебто бджоли, будуючи свої стільники, користуються складними математичними обчисленнями. Побудовані ними без усяких креслень стільники з найбільшою точністю відтворили розміри ідеальної споруди розрахованої за всіма правилами науки.

Будуючи шестикутні чарунки, бджоли найбільш економно використали стільники при найменшій витраті воску. Отже, бждоли, не знаючи математики, правильно “визначили”, що правильний шестикутник матиме найменший периметр.

 « Далее этой ступени совершенства в архитектуре естественный отбор не мог вести, потому что соты пчёл абсолютно совершенны с точки зрения экономии труда и воска» Чарльз Дарвін

Правильні многокутники у вишивці

Правильні многокутники в мозаїці

Правильні многокутники в плитці

З давніх-давен правильні многокутники застосовуються в архітектурі, у живопису. Правильні чотирикутники, шестикутники і восьмикутники зустрічаються в старовинних вавілонських і єгипетських пам’ятках у вигляді зображень на стінах, прикрас, викарбуваних з каменю.

Правильні многокутники в архітектурі Національна бібліотека в Білорусії, Мінськ. В основі будівлі – правильний шестикутник У Вашингтоні одна з будівель побудована у формі правильного п’ятикутника

В живому світі ми можемо розгледіти правильні многокутники

В рослинному світі ми теж можемо розгледіти правильні многокутники

Сніжинки падають на землю правильними шестикутниками. Природа ще раз підтверджує нам свою досконалість.

Калейдоскоп, дитяча гра, в якій зачаровують симетричні узори, що змінюються

Правильні многокутники в дитячих іграшках

Правильні многокутники в повсякденному житті

Правильні многокутники в повсякденному житті

Правильні многокутники в смачних стравах

Задача В кондитерському цеху зробили круглий торт радіусом 18 см. Для пакування є два види коробок: квадратної форми і форми правильного шестикутника. В яку коробку помістимо торт, якщо сторона квадратної коробки 36 см, а шестикутної – 20 см ?

Правильні многокутники З часів Піфагора відомі вони. У них рівні сторони, рівні кути. Зустрінемо в орнаментах і на паркетах, І у віршах відомих поетів. І навіть бджоли з ними працюють, І мед для здоров’я нам пропонують!

Домашнє завдання. Основний рівень №260(3), №264(3), №268(3). Достатній рівень №273(2), №276(2), №277(2), №278(2)