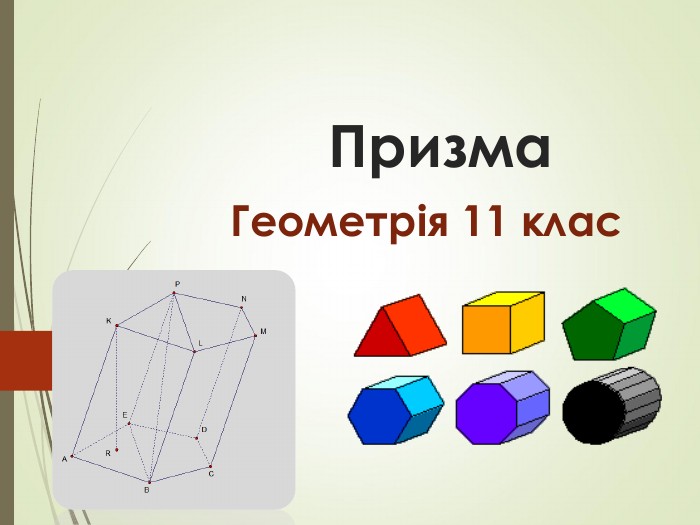
Презентація до уроку геометрія в 11 класі тема "Призма "
Про матеріал
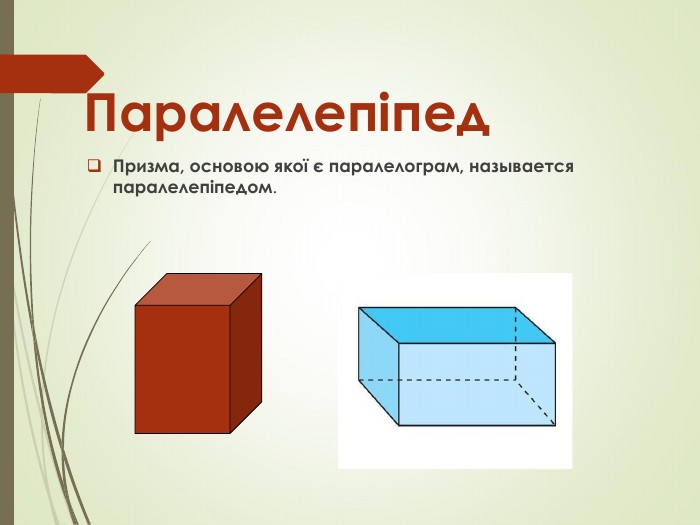
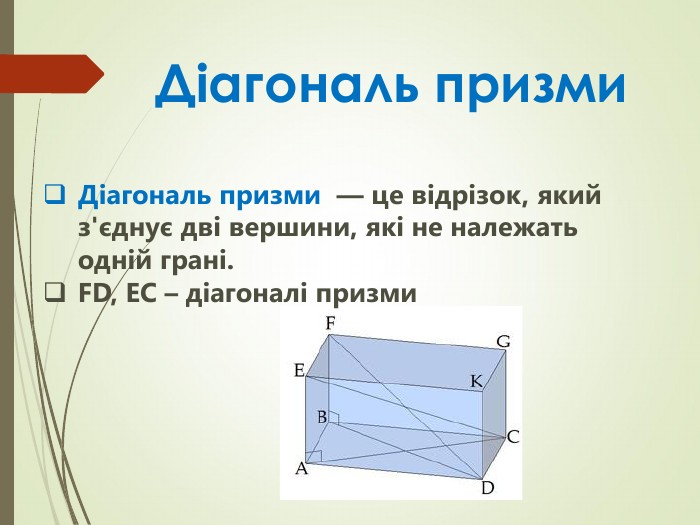
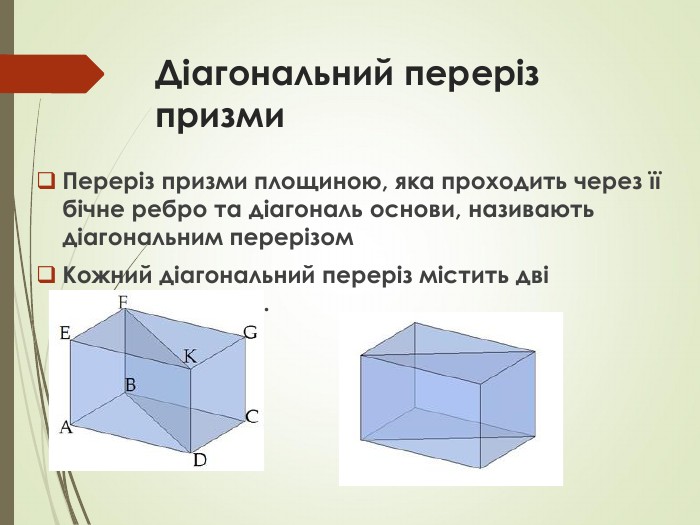
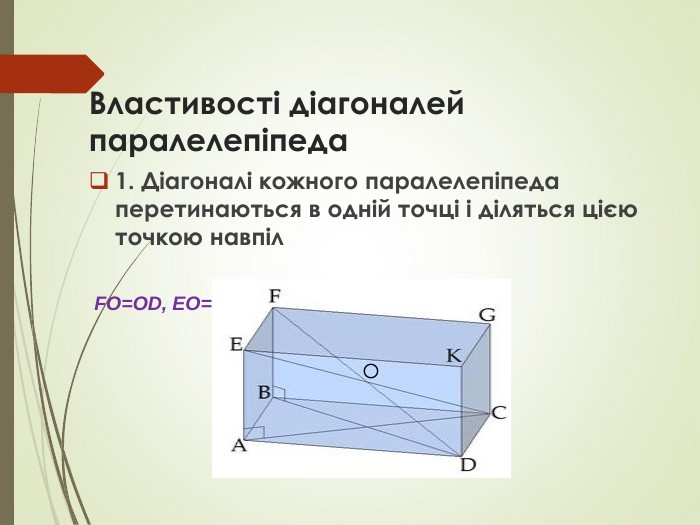
Презентація до підручника Математика 11 клас Г.Бевз В.Бевз рівень стандарту. Дана презентація є доповненням до вивчення параграфа 17 теми Призма Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку












-

Решетнік Галина
23.09.2024 в 23:45
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Іванів Ольга Василівна
19.09.2024 в 10:52
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Клепікова Ольга Анатоліївна
16.09.2024 в 23:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Scherban Tatyana
24.04.2023 в 17:13
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 1 відгук