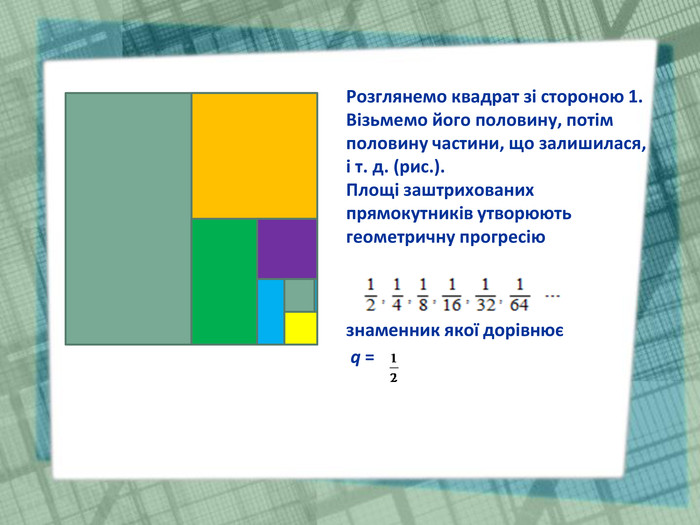
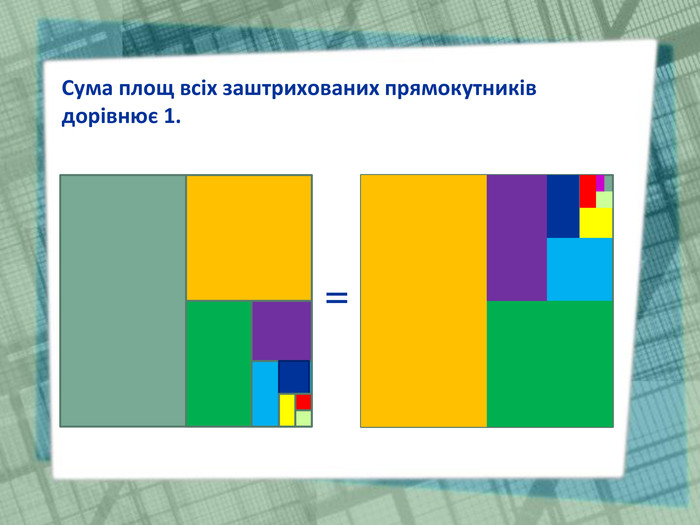
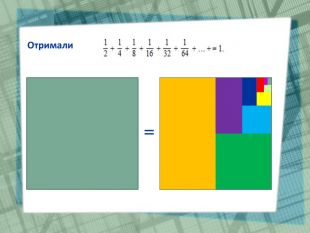
Презентація до уроку "Нескінченна спадна геометрична прогресія"
Про матеріал
У презентації візуалізовано формулу суми нескінченної спадної геометричної прогресії. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку