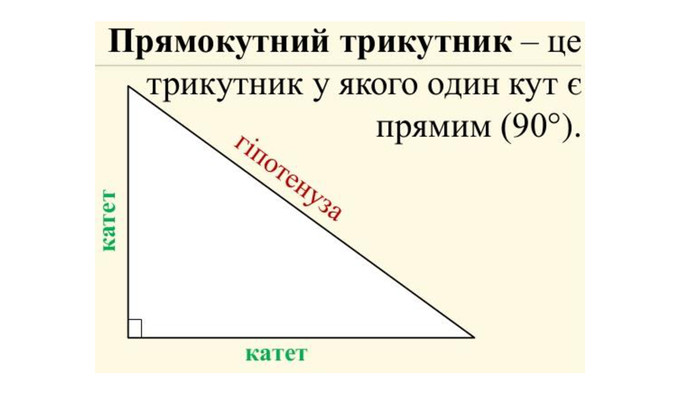
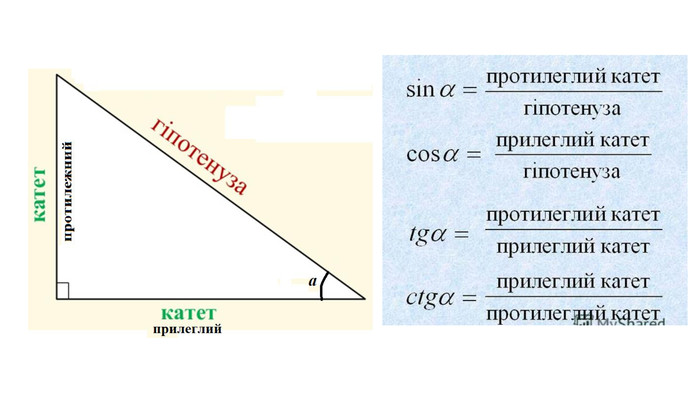
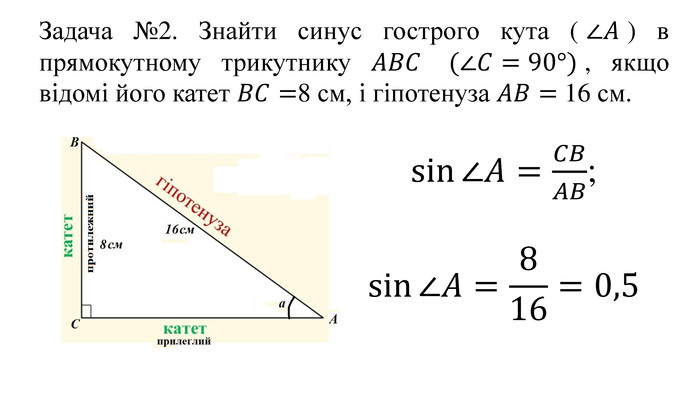
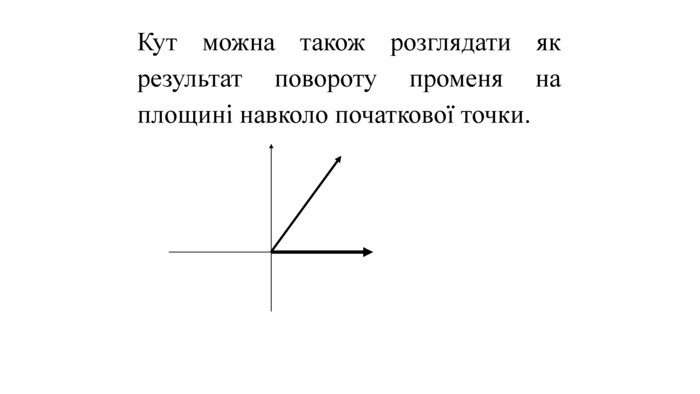
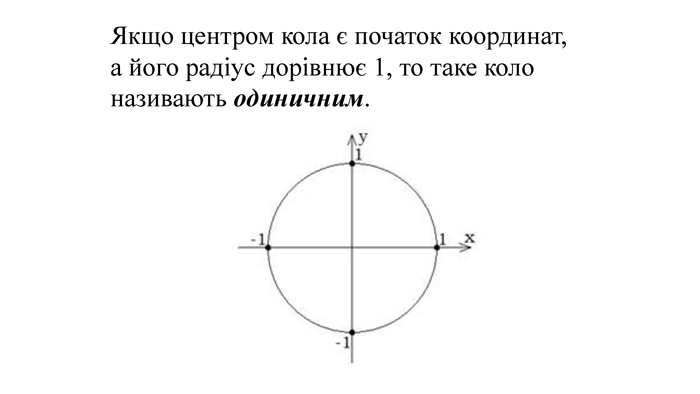
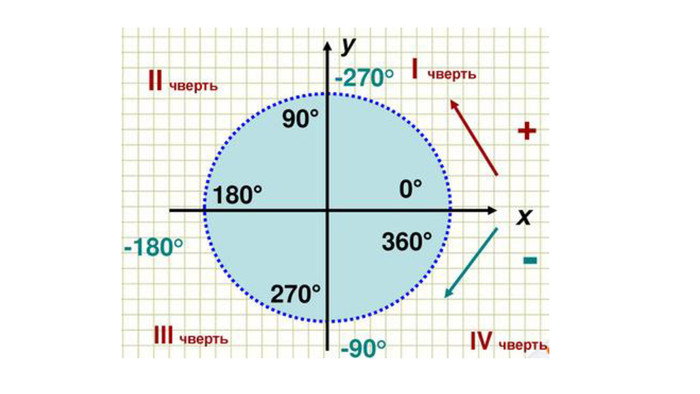
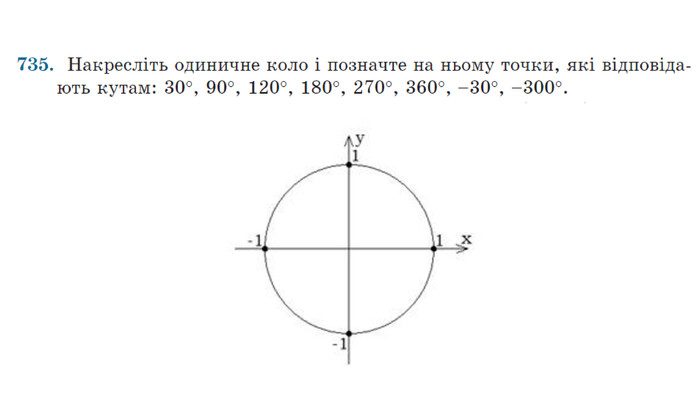
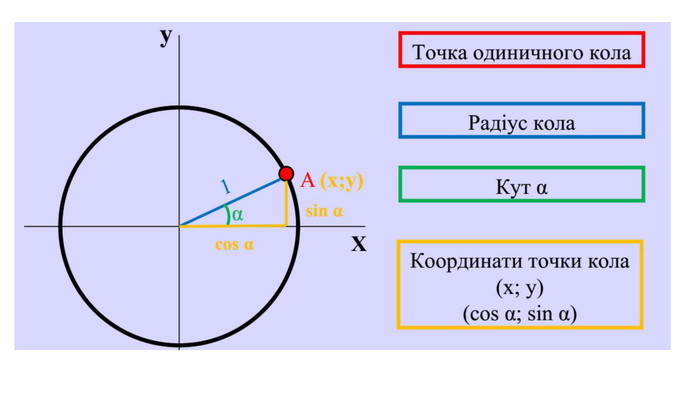
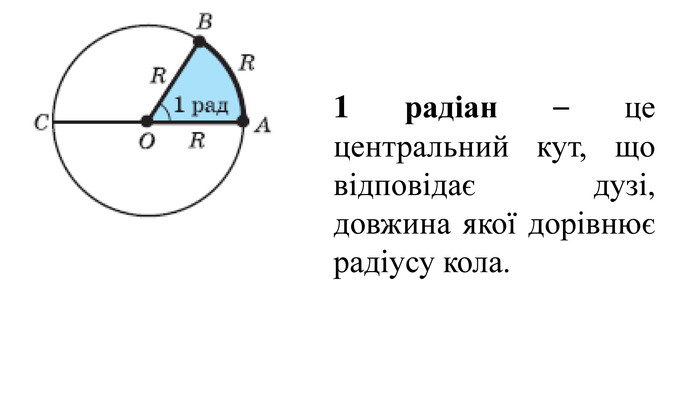
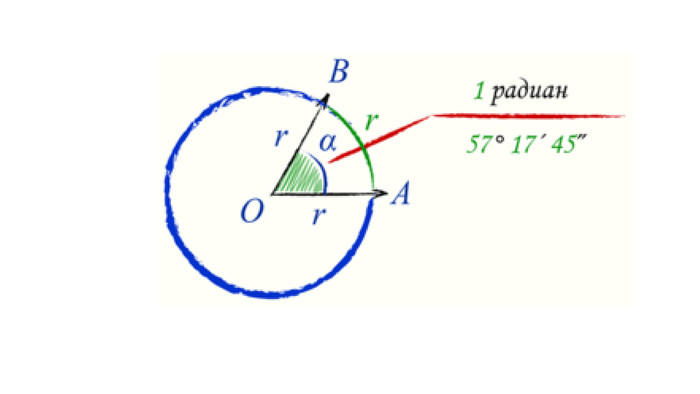
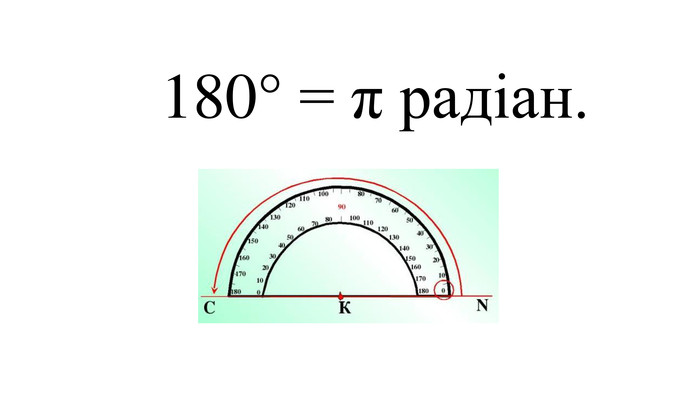
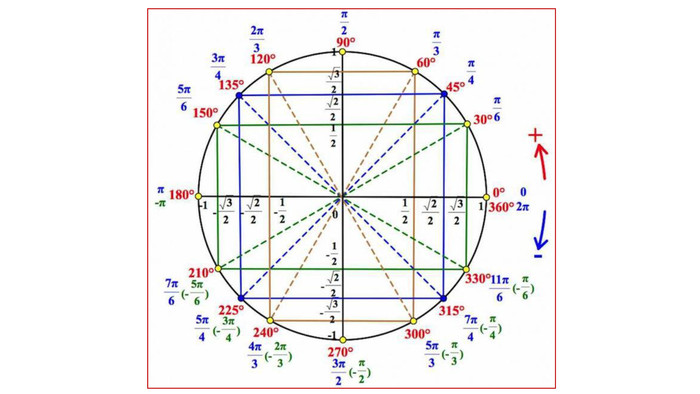
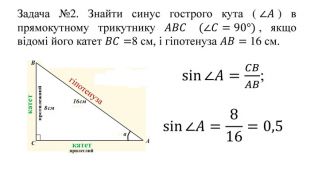
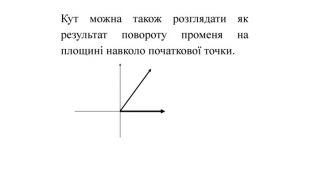
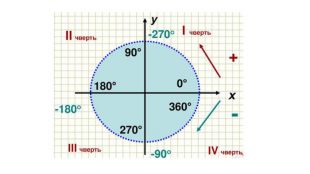
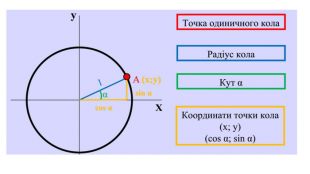
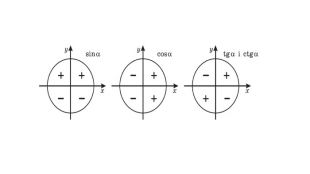
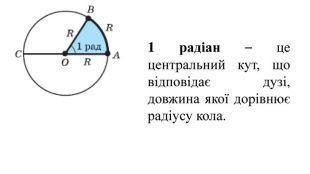
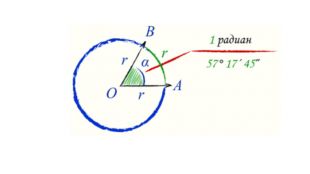
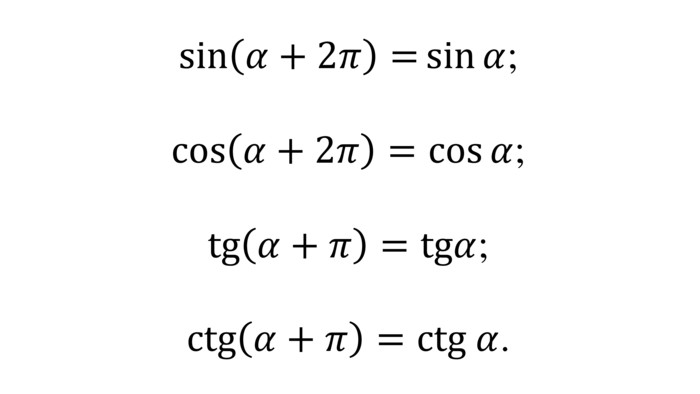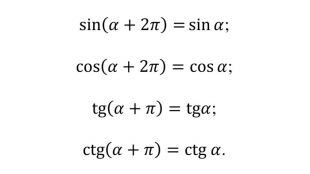Введення означень тригонометричних функцій довільного кута кута
Про матеріал
Презентація містить містить основні матеріали для введення означень тригонометричних функцій довільного кута кута Перегляд файлу
Зміст слайдів

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку