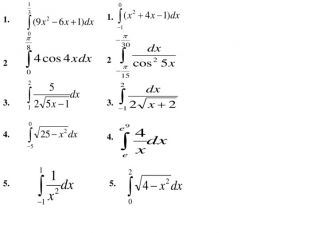Презентація до уроку " Визначений інтеграл"



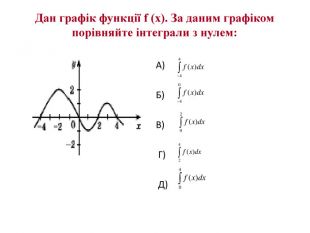
![№ 3 Обчислити На [-2; 2], |x – 2| = - x + 2 На (2; 3], |x – 2| = x - 2 Рішення x 3 2 - 2 № 3 Обчислити На [-2; 2], |x – 2| = - x + 2 На (2; 3], |x – 2| = x - 2 Рішення x 3 2 - 2](/uploads/files/280062/160941/173578_images/5.jpg)



















![Рассмотрим решение задачи на перемещение материальной точки Предположим, что точка движется по прямой (по оси ОХ) и нам известна скорость этой точки. Перемещение точки по оси будем считать функцией времени: s=s(t). Как найти перемещение точки за промежуток времени [t1 ; t2]? Рассмотрим решение задачи на перемещение материальной точки Предположим, что точка движется по прямой (по оси ОХ) и нам известна скорость этой точки. Перемещение точки по оси будем считать функцией времени: s=s(t). Как найти перемещение точки за промежуток времени [t1 ; t2]?](/uploads/files/280062/160941/173578_images/34.jpg)
![Если скорость точки постоянна и равна V, то перемещение вычисляется так: S = V·t Пусть теперь эта скорость меняется и нам задан закон этого изменения V=V(t). Рассмотрим перемещение на отрезке времени [t; t+dt]. Если скорость точки постоянна и равна V, то перемещение вычисляется так: S = V·t Пусть теперь эта скорость меняется и нам задан закон этого изменения V=V(t). Рассмотрим перемещение на отрезке времени [t; t+dt].](/uploads/files/280062/160941/173578_images/35.jpg)

![Рассмотрим пример: Материальная точка движется со скоростью: Вычислить перемещение за промежуток времени [1;2] секунды Рассмотрим пример: Материальная точка движется со скоростью: Вычислить перемещение за промежуток времени [1;2] секунды](/uploads/files/280062/160941/173578_images/37.jpg)




№ 1 Рішення F (x) = x2 + 4x + c - загальний вигляд первісних функції f. Оскільки парабола і дотична мають тільки одну спільну точку, то рівняння x2 + 4x + c = 6х + 3 має єдиний корінь (D = 0), тоді x2 - 2x + c - 3 = 0 D1 = 1 - c + 3 = - з + 4, - з + 4 = 0, с = 4 Отже, F (x) = x2 + 4x + 4 Домашня робота Знайти ту первісну функції f(x) = 2x + 4, графік якої дотикається прямої у = 6х + 3
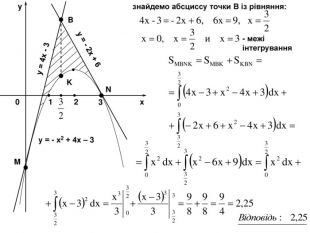
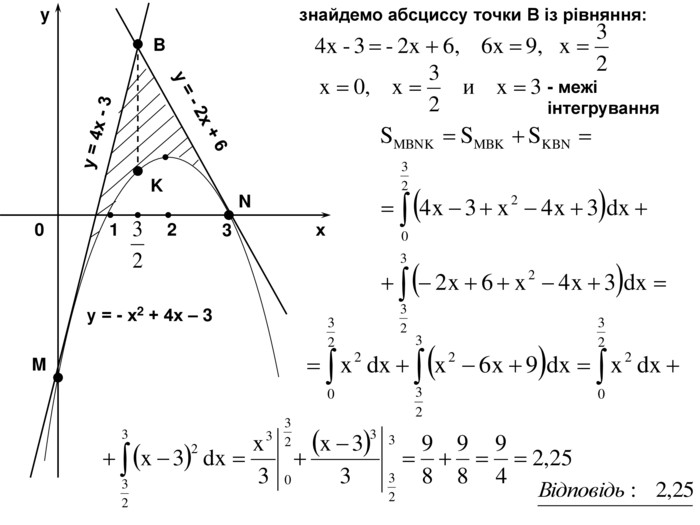
Рішення Знайдемо рівняння дотичних до графіка функції f (x) = - x2 + 4x - 3 в точках х = 0 і х = 3. y = f (x0) + f '(x0) (x - x0) - рівняння дотичної в загальному вигляді Обчислити площу фігури, обмеженою параболою у = - х2 + 4х - 3 і дотичними до неї в точках з абсцисами х = 0 і х = 3. x0 = 0 1) f(0) = - 3 2) f ‘(x) = - 2x + 4 3) f ‘(0) = 4 4) y = - 3 + 4(x – 0) y = 4x – 3 x0 = 3 1) f(3) = - 9 + 12 – 3 = 0 2) f ‘(3) = - 2 3) y = - 2(x – 3) y = - 2x + 6 Будуємо графіки функцій у = - х2 + 4х – 3, y = 4x – 3, y = - 2x + 6 в одній системі координат: у = - х2 + 4х - 3 - графіком є парабола. (2; 1) - вершина параболи
Уже Архімед успішно знаходив площі фігур, незважаючи на те, що в математиці його часу не було поняття інтеграла. Але лише інтегральне числення дає загальний метод вирішення завдань з різних областей наук. Недарма навіть поети оспівували інтеграл Сенс - там, де змії інтеграла Між цифр і букв, між d і f. Там - влада, там творчі сурми! Перед волею чисел усі - раби. І сонця шлях вершать, покірні Німим промов і ворожби. В. Брюсов.
Ми з вами вивчали інтеграл і його властивості. Філософське висловлювання Гільберта: «У кожної людини є певний світогляд. Коли цей кругозір звужується до нескінченного малого, то він звертається в точку. Тоді чоловік і каже що це і є його точка зору.» Давайте спробуємо виміряти точку зору на застосування інтеграла!
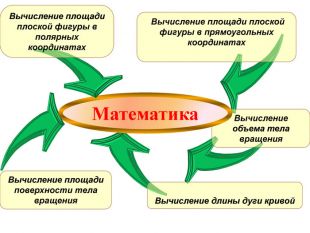
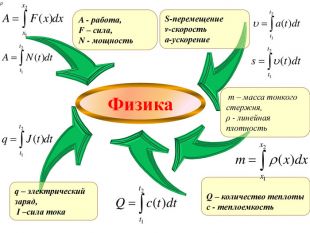
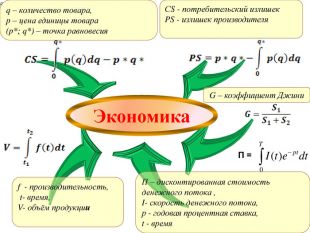
СS - потребительский излишек PS - излишек производителя G – коэффициент Джини f - производительность, t- время, V- объём продукции Экономика q – количество товара, p – цена единицы товара (p*; q*) – точка равновесия П – дисконтированная стоимость денежного потока , I- скорость денежного потока, р - годовая процентная ставка, t - время . П =
Домашнє завдання. Завдання: Перед будівлею школи вирішено розбити клумбу. Але за формою клумба не повинна бути круглою, квадратною або прямокутною. Вона повинна містити в собі прямі і криві лінії. Нехай вона буде плоскою фігурою, обмеженою лініями Y = +2; X = 4; Y = 6. Необхідно ще підрахувати скільки грошей можна отримати за копання цієї клумби, якщо за кожен мІ виплачують 50 грн ...?


про публікацію авторської розробки
Додати розробку