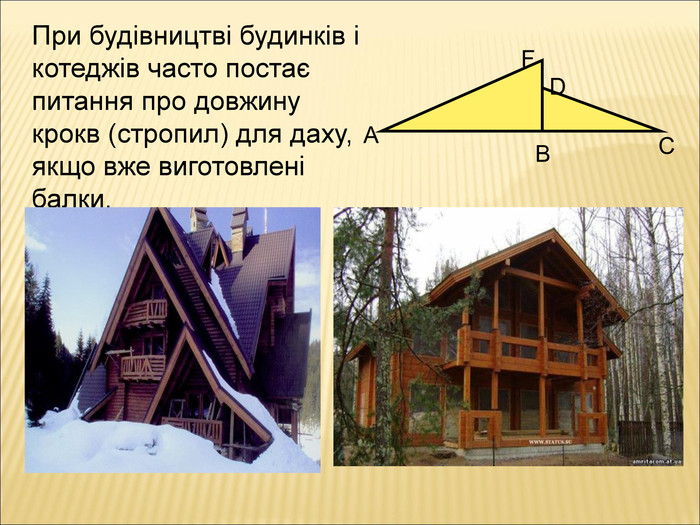
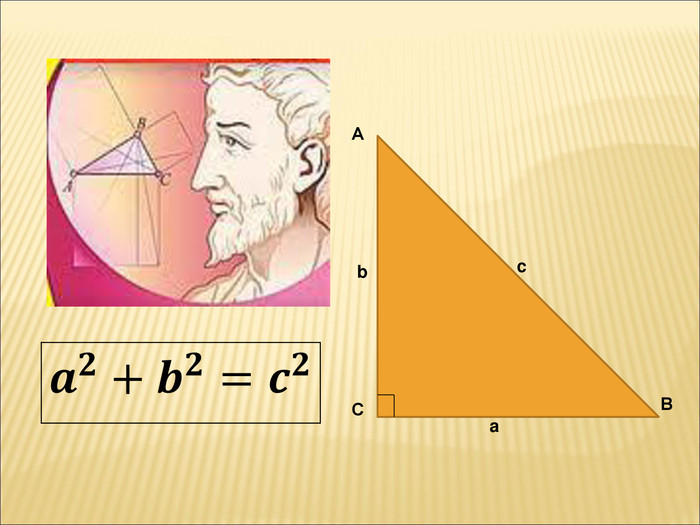
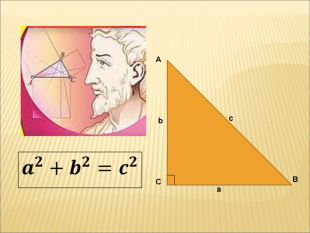
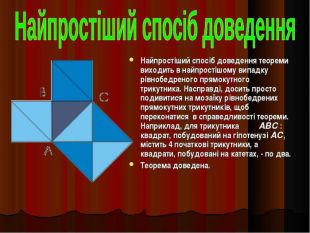
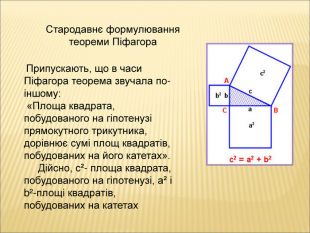
Презентація до уроку " Теорема Піфагора"
Про матеріал
Розрорбка уроку у вигляді презентації. Тема, мета, мотивація, формули, задачі, рефлексія. Перегляд файлу
Зміст слайдів
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку