Презентація до уроку " Застосування подібності трикутників"
Про матеріал
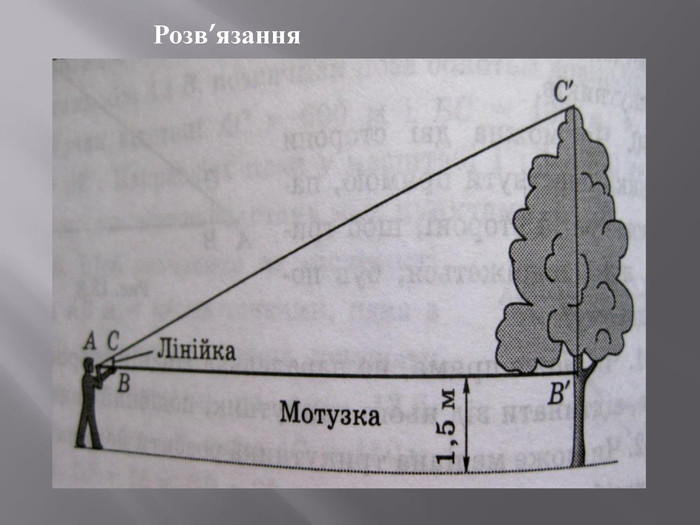
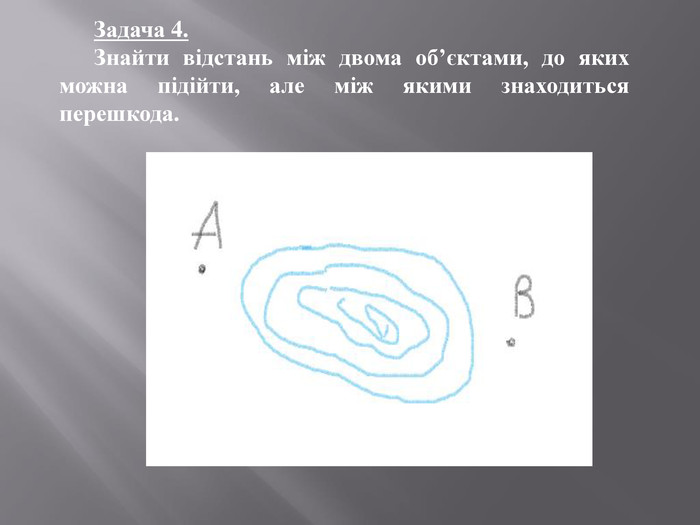
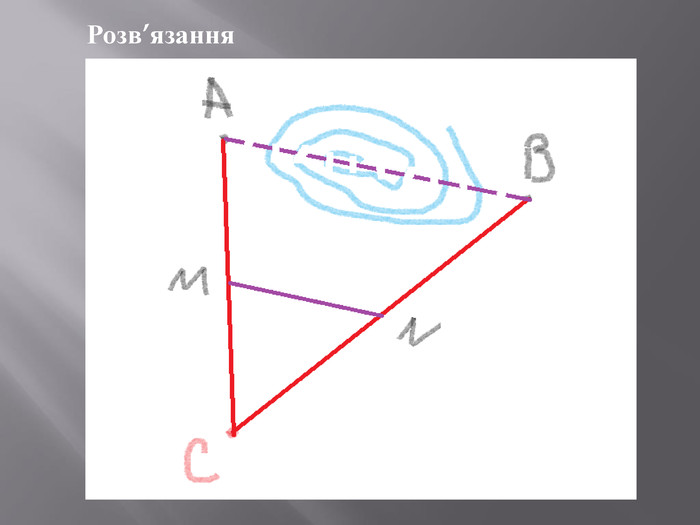
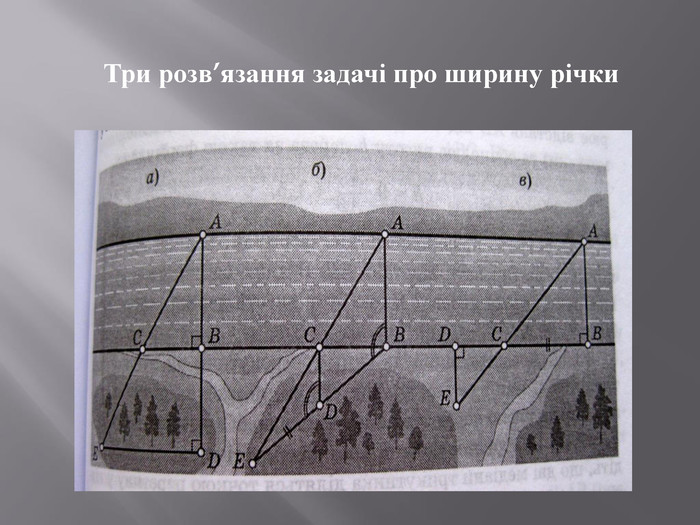
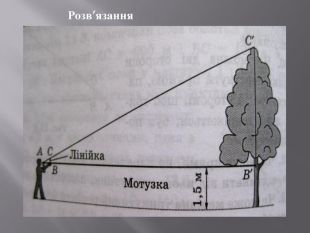
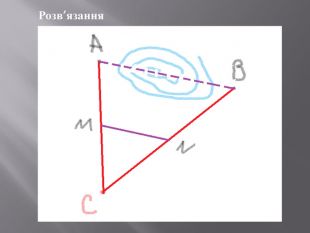
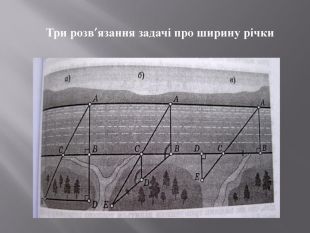
Презентація, яка містить практичні задачі та їх розвязки на застосування подібності трикутників та фотогріфії міні-проєкту . Перегляд файлу
Зміст слайдів
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку