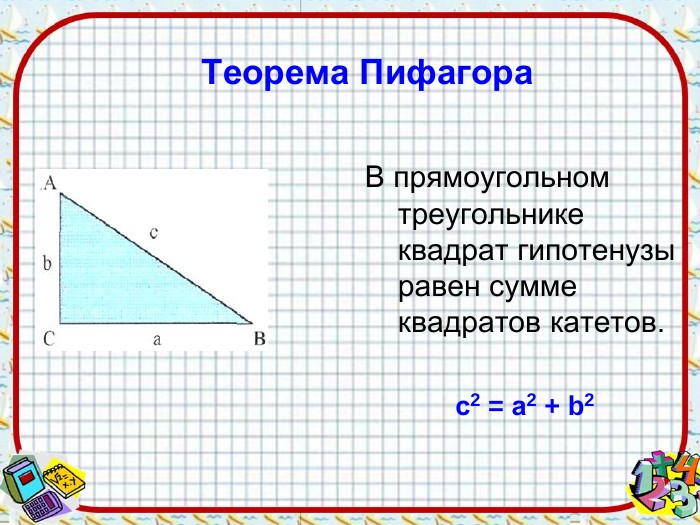
Презентація до уроку "Теорема Піфагора"

Тема урока:«Теорема Пифагора» 8-А класс

«Геометрия обладает двумя великими сокровищами. Первое – это теорема Пифагора…»

Цели:узнать, кто такой Пифагор;в чём заключается теорема Пифагора;доказать теорему разными способами;показать практическое применение;научиться решать задачи с применением теоремы Пифагора

Кто быстрее?Какой треугольник называется прямоугольный?Что такое гипотенуза?Что такое катеты?Сформулировать теорему Пифагора. Как называется треугольник со сторонами 3см, 4см, 5см.

Команды:«Историки»«Теоретики»«Практики»

История о Пифагоре: Пифагор родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море, поэтому его называют Пифагором Самосским. Его отец был резчиком по камню. Ещё в детстве Пифагор проявлял незаурядные способности, и когда подрос, воображению юноши стало тесно на маленьком острове.

Пифагор перебрался в г. Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Мудрый учёный посоветовал юноше отправиться в Египет. Когда Пифагор постиг науку египетских жрецов, то отправился домой, чтобы там создать свою школу. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками.

История теоремы: Изучение вавилонских клинописных таблиц и древних китайских рукописей показало, что это утверждение было известно задолго до Пифагора. Заслуга же Пифагора состояла в том, что он открыл доказательство этой теоремы. Согласно одной из легенд, знаменитую теорему Пифагор добыл как выигрыш с неизвестным математиком. Тот отдал свиток с теоремой Пифагору и сказал, что человек, который владеет этим свитком, будет известным не одно тысячелетие…

Теорему называли «мостом ослов», так как слабые ученики, заучивающие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.

Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. с2 = а2 + b2

Алгебраическое доказательство:1) Проведем высоту CD из вершины прямого угла С.2) По определению косинуса угла соs. А=AD/AC=AC/AB, отсюда следует AB*AD=AC2.3) Аналогично соs. В=BD/BC=BC/AB, значит AB*BD=BC2.4) Сложив полученные равенства почленно, получим: AC2+BC2=АВ*(AD + DB)AB2=AC2+BC2. САВД

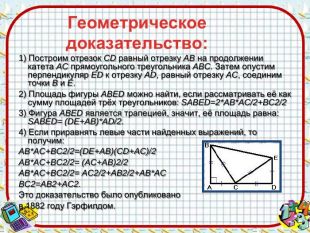
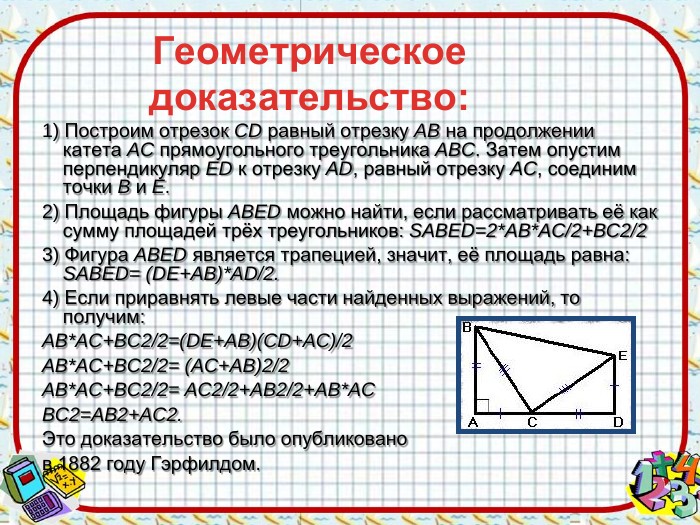
Геометрическое доказательство:1) Построим отрезок CD равный отрезку AB на продолжении катета AC прямоугольного треугольника ABC. Затем опустим перпендикуляр ED к отрезку AD, равный отрезку AC, соединим точки B и E. 2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников: SABED=2*AB*AC/2+BC2/23) Фигура ABED является трапецией, значит, её площадь равна: SABED= (DE+AB)*AD/2.4) Если приравнять левые части найденных выражений, то получим: AB*AC+BC2/2=(DE+AB)(CD+AC)/2 AB*AC+BC2/2= (AC+AB)2/2 AB*AC+BC2/2= AC2/2+AB2/2+AB*ACBC2=AB2+AC2. Это доказательство было опубликовано в 1882 году Гэрфилдом.

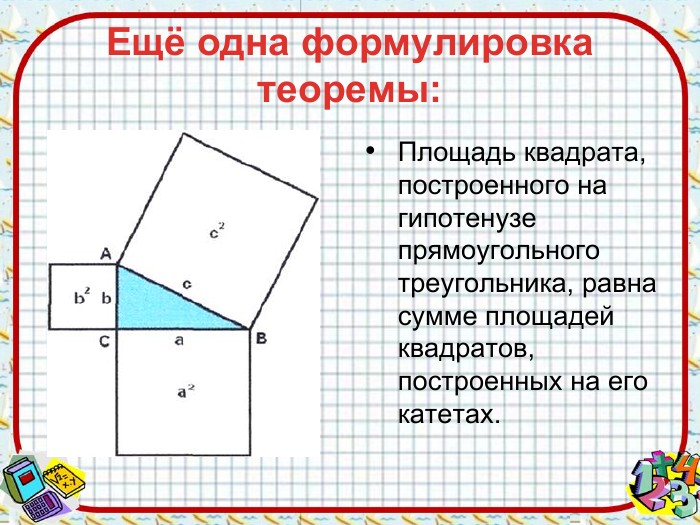
Древнекитайское доказательство1) На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами a, b и гипотенузой с уложены так, что их внешний контур образует квадрат со стороной a+b, а внутренний – квадрат со стороной с, построенный на гипотенузе2)Площадь квадрата равна ( а + b)²3)С другой стороны квадрат составлен из четырёх равных прямоугольных треугольников с площадью ½ аb и квадрата, площади с²4) S=4 *1/2ab + с2 = 2bc + с2. (а+b)2 =2ab+ с2. с2 = а2 + b2.

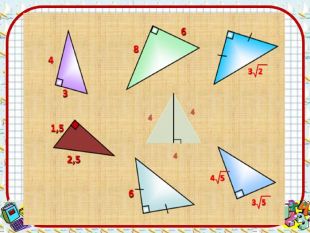
Теорема, обратная к теореме Пифагора:позволяет проверить, является ли тот или иной треугольник прямоугольным. Этим пользовались землемеры и строители Древнего Египта: они размечали прямые углы с помощью веревки, разделенной узлами на 12 равных кусков;прямоугольный треугольник со сторонами 3, 4, 5 называется «египетским», а тройки (a, b, c) натуральных чисел, удовлетворяющие уравнению c2 = a2 + b2, т. е. служащие длинами сторон прямоугольных треугольников, Пифагоровыми.

Некоторые Пифагоровы тройки: (3,4,5), (6,8,10), (5,12,13), (9,12,15), (8,15,17), (12,16,20), (15,20,25), (7,24,25), (10,24,26), (20,21,29), (18,24,30),(10,30,34), (21,28,35), (12,35,37), (15,36,39), (24,32,40), (9,40,41), (27,35,45), (14,48,50), (30,40,50)…

Ещё одна формулировка теоремы: Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.

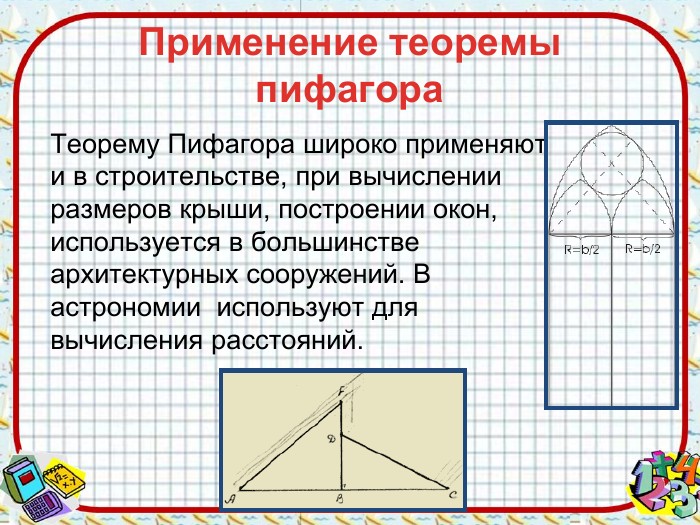
Применение теоремы Пифагора В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем надежнее связь, чем больше зона покрытия, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе.

Мобильная связь. Какую наибольшую высоту должна иметь антенна мобильного оператора, чтобы передачу можно было принимать в радиусе R=200 км? (радиус Земли равен 6380 км.)Решение: Пусть AB= x, BC=R=200 км, OC= r =6380 км. OB=OA+ABOB=r + x. Используя теорему Пифагора, получим ответ: 2,3 км.

Применение теоремы пифагора. Теорему Пифагора широко применяют и в строительстве, при вычислении размеров крыши, построении окон, используется в большинстве архитектурных сооружений. В астрономии используют для вычисления расстояний.

Интересное о Пифагоре: Пифагор – это на самом деле прозвище, а не имя (Пифагор - "убеждающий речью"). Увлекался спортом, побеждал в кулачном бою на Олимпийских играх. Придумал специальную кружку, которая заставляла пить только в ограниченных количествах. Сегодня она продается на Родосе, Самосе и Крите как сувенир. Пифагор считал, что нельзя употреблять пищу животного происхождения. Он верил, что в животных переселяются души людей.

Важные открытия, связанные с именем Пифагора:в географии и астрономии – представление о том, что Земля – шар и что существуют другие, похожие на неё миры;в музыке – зависимость между длиной струны арфы и звуком, который она издаёт;в геометрии – построение правильных многоугольников (один из них пятиконечная звезда – стал символом пифагорейцев).

Валеологическая пауза

Работа в группах

Задача. I группа. Из одной точки проведены к данной прямой перпендикуляр и две наклонные. Найдите длину перпендикуляра, если наклонные равны 41см и 50см, а их проекции на данную прямую относятся как  3 : 10.

Задача. II группа. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки, равные 5 и 12. Найдите катеты треугольника.

Задача. III группа. На расстоянии 20 метров друг от друга растут две сосны высотой 8 и 23 метра. Определите расстояние между их вершинами.

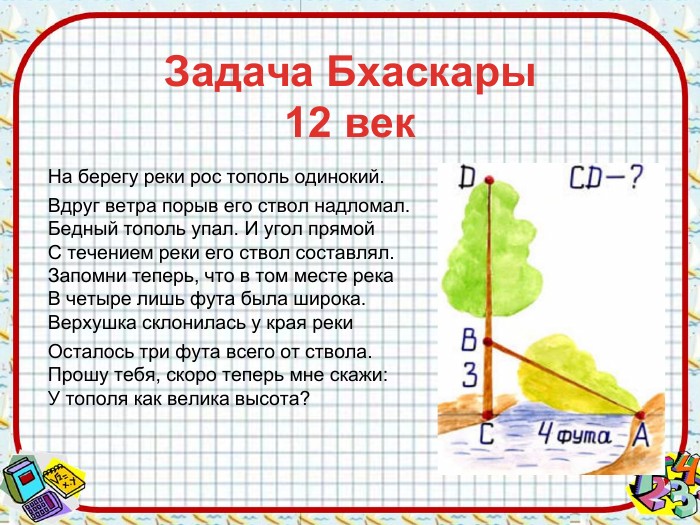
Задача Бхаскары 12 век. На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой. С течением реки его ствол составлял. Запомни теперь, что в том месте река. В четыре лишь фута была широка. Верхушка склонилась у края реки. Осталось три фута всего от ствола. Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?

Тестування. В Classtime

Если дан нам треугольник. И притом с прямым углом,То квадрат гипотенузы. Мы всегда легко найдём: Катеты в квадрат возводим,Сумму степеней находим – И таким простым путём. К результату мы придём.

Рефлексия: Сегодня на уроке мы: Повторили…Узнали…Научились…

Домашнее задание:1) найти ещё один способ доказательства теоремы Пифагора;2) найти 5 задач по теореме Пифагора и решить их с сайта https://testportal.gov.ua/testy-mynulyh-rokiv/ (подготовка к ВНО)

Математика присутствует во всем: она и в строении растения, она и в теле человека, она и в музыке, и по ее законам строится вселенная. Математика – это не только сухие формулы, но это еще и красота. Вы видите, как тесно, почти неразрывно связаны математика и законы прекрасного, что законы красоты носят математический характер. Природа говорит на языке математики!

Релаксация