Розробка уроку з геометрії на тему "Відстані у просторі"

Державний навчальний заклад

«Мукачівський центр професійно-технічної освіти»

 

 

 

 

 

 

 

 

Відкритий урок

 з математики:

 

 

 

«Відстані у просторі»

 

 

 

 

 

 

 

 

Підготувала

викладач математики

 Петах Вікторія Йосипівна

 

 

 

 

 

 

 

 

 

 

 

Мукачево 2015 р.

Тема уроку. Відстані в просторі.

Мета уроку: Сформувати поняття відстані від прямої до паралельної їй площини, між паралельними площинами, про властивості точок прямої, паралельної площині, про властивості точок площини, паралельної даній площині. Сформувати поняття  спільного перпендикуляра двох мимобіжних прямих, відстані між мимобіжними прямими; сформувати вміння застосовувати ці знання при розв’язуванні задач.

Тип уроку: засвоєння нових знань і вироблення вмінь.   

Хід уроку

І. Організаційний етап

ІІ. Перевірка домашнього завдання

Учні перевіряють правильність виконання домашнього завдання.

Задача. Знайдіть кут між діагоналлю куба і мимобіжною з нею діагоналлю основи куба.

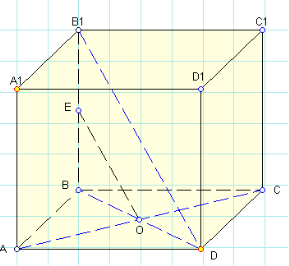
Розв’язання

Шуканий кут буде таким же ж, як кут між ОЕ – середньою лінією трикутника DBB₁ та прямою АС, тобто становитиме 90⁰, бо використовуючи теорему про три перпендикуляри з умови BB₁(ABC), BDAC маємо, що EOAC

ІІІ. Формулювання теми, мети і завдань уроку.  Мотивація навчальної діяльності.

Учні записують перші літери слів, які є відповідями на запитання в табличку (Додаток 1) для того, щоб дізнатися теми уроку, перевіривши один одного викладають оцінки і здають викладачу таблички.

Дешифровщик

ЗАПИТАННЯ:

1.               Частина прямої, що лежить між двома точками.
2.               Чорна, червона, кабачкова.
3.               Хорда, що проходить через центр кола.
4.               Розділ геометрії, який вивчаємо.
5.               Твердження, що потребує доведення.
6.               Твердження, що не потребує доведення.
7.               5-5=
8.               Сухофрукт із винограду.
9.               Навчальне заняття; певний проміжок часу для заняття учнів з окремого предмета.
10.          Відрізок, що сполучає дану точку з точкою площини і лежить на прямій перпендикулярній до площини.
11.          Результат віднімання.
12.          Як називаються паралельні сторони трапеції?
13.          Відношення протилежного катета до гіпотенузи у прямокутному трикутнику.
14.          Рівнобедрений . . .
15.          … координат.
16.          Чотирикутник, всі сторони якого рівні.
17.          М’ясо птиці, не курятина.

1    В	2   І	3    Д	4    С	5    Т	6    А	7    Н	8   І
			9    У
10  П	11  Р	12  О	13  С	14  Т	15  О	16  Р	17  І

Надзвичайно важливим є поняття відстані в просторі : між  точками, прямими, площинами, геометричними множинами точок, тілами.

IV.Формування знань

Використовуючи листок-трафарет (Додаток 2) та супроводжуючу завдання презентацію, учні виконують практичні завдання та повторюють основні поняття по знаходженню відстаней

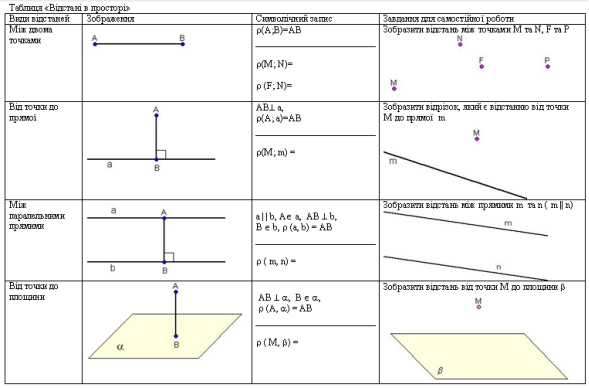
• між двома точками
• від точки до прямої
• між паралельними прямими
• від точки до площини

Таким чином йде підготовка до вивчення нового матеріалу на основі узагальнення і повторення вивченого раніше.

Після цього йде  введення нових понять:  означення та знаходження відстаней

• від прямої до паралельної їй площини
• між паралельними площинами
• між мимобіжними прямими

 

V. Пояснення нового матеріалу.

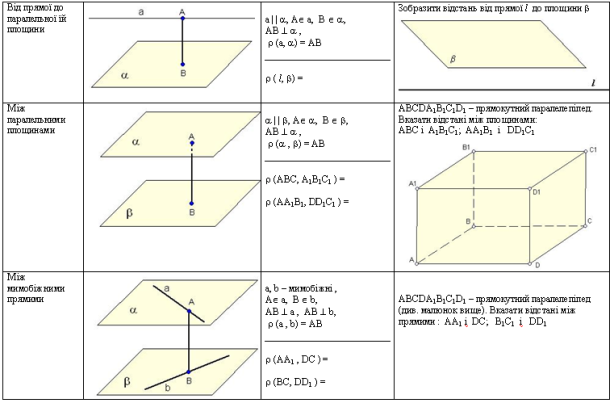
В ході пояснення виконуються практичні завдання (див. таблицю 2).

Учні записують в зошит формулювання нових теорем (теореми 2, 3 та 4).

Теорема 2 (про відстань між паралельними прямою і площиною)

Відстань між паралельними прямою і площиною дорівнює довжині спільного перпендикуляра, проведеного з будь-якої точки прямої на площину.

AB ,   B  ,  (A; )=AB

Теорема 3 (про відстань між паралельними площинами)

Відстань між паралельними площинами дорівнює довжині спільного перпендикуляра, проведеного з будь-якої точки однієї площини на другу.

ǁ,   , B  , AB , (,)=AB

Теорема 4

Дві мимобіжні прямі мають спільний перпендикуляр і до того ж тільки один. Він є спільним перпендикуляром до паралельних площин, які проходять через ці прямі.

a, b – мимобіжні,   a, B   b, AB a, AB b, (a, b)=AB

VI. Ознайомлення із способами знаходження відстані між мимобіжними прямими

Спосіб 1. Знаходження спільного перпендикуляра

В ході розв’язання відшукують або будують спільний перпендикуляр до даних мимобіжних прямих і обчислюють його довжину

Задача 1. Ребро куба дорівнює а. Знайти відстань між прямими ВC і DD₁

( відрізок CD довжиною а)

 

Задача 2. Ребро куба дорівнює а. Знайти відстань між прямими AA₁ і CB₁

( відрізок A₁B₁ довжиною а)

 

Спосіб 2. Побудова паралельних площин

В ході розв’язання  проводять через дані мимобіжні прямі паралельні площини    і  ; тоді шукана відстань дорівнює відстані між цими площинами

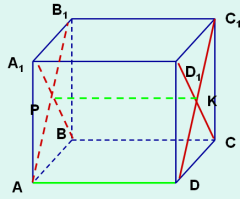Задача 3. Ребро куба дорівнює а. Знайти відстань між діагоналями несуміжних граней -  прямими A₁В і DC₁

 

( відрізок РК, що сполучає центри граней AA₁B₁ та CС₁D довжиною а)

 

 

 

Спосіб 3. Побудова  однієї паралельної площини

В ході розв’язання  проводять через одну з даних мимобіжних прямих b площину , паралельну другій прямій a; тоді шукана відстань дорівнює відстані між прямою a і паралельною їх площиною 

Задача 4. Ребро куба дорівнює а. Знайти відстань між діагоналлю основи та несуміжним до неї бічним ребром -  прямими A₁С₁ і DD₁

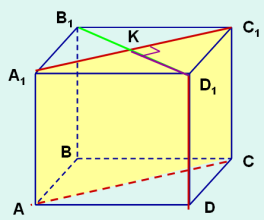
Розв’язання

Проведемо через діагональ A₁C1

 верхньої грані куба площину,

паралельну до бічного ребра DD₁-

площину AA₁C.

AA₁    (AA₁C), AA₁ ║ DD₁, тому

DD₁ ║ (AA₁C)

Так як діагоналі квадрата взаємно

перпендикулярні (A₁C₁  B₁D₁)

а також взаємно перпендикулярні основи та побудована діагональна

площина, то КD₁ – шуканий перпендикуляр і шукана відстань,

де К – точка перетину діагоналей основи  

(A₁С₁, DD₁)=KD₁=

Спосіб 4. Побудова перпендикулярної площини

Проводять площину , перпендикулярну до однієї з даних  прямих a;  і ортогонально проектують обидві дані прямі на цю площину; тоді проекцією прямої a є точка А перетину цієї прямої з площиною  , проекцією прямої b – деяка пряма b₁ площини , а шукана відстань дорівнює відстані від точки А до прямої b₁

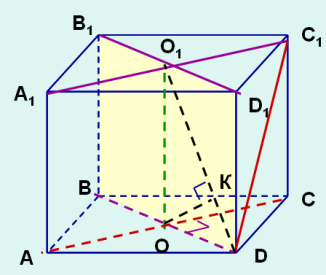Задача 5. Ребро куба дорівнює а. Знайти відстань між мимобіжними діагоналями суміжних граней куба -  прямими AС і DС₁

Розв’язання

Використаємо перпендикулярність діагоналей квадратів основ куба

Проведемо через діагональ BD площину, перпендикулярну до діагоналі АС, - площину BB₁D.  Ортогональними проекціями на неї прямих AС та DC₁  будуть точка О (перетин АС і BD)  та пряма DO₁

Опустимо перпендикуляр ОК з точки  О на пряму О₁D ОК – шукана відстань

Так як OKO₁D=OO₁ OD, маємо

 

 

 

 

 

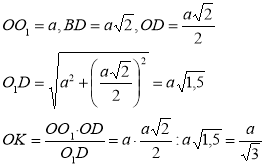
VІI. Підбиття підсумків уроку.

Учні підбивають свої бали і здають викладачеві свої результати.

VIII. Домашнє завдання.

Задача 6. Рівні прямокутники ABCD і ABC₁D₁ лежать у перпендикулярних площинах. Знайдіть відстань між мимобіжними прямими AD₁ і С₁D , якщо АВ=15 см, ВС=20 см

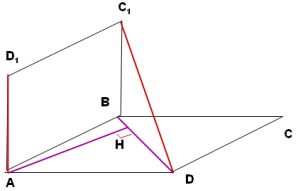Розв’язання

Оскільки D₁A і C₁В – перпендикуляри до прямої  перетину двох перпендикулярних площин, то D₁A (АВС), С₁В (АВС).

Побудуємо ортогональні проекції прямих AD₁ і С₁D на площину АВС. Проекціями є відповідно точка А та пряма BD. Шукана відстань дорівнює висоті АН прямокутного трикутника ABD (A=90⁰)

Оскільки за теоремою Піфагора ВD=25 см,  то

Відповідь: 12 см