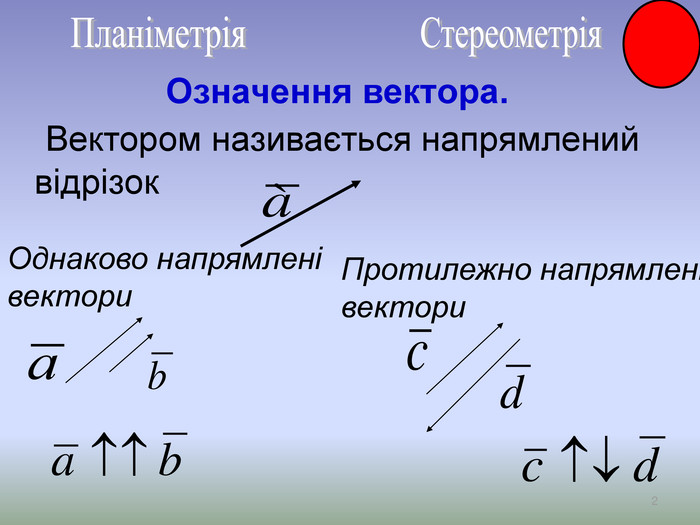
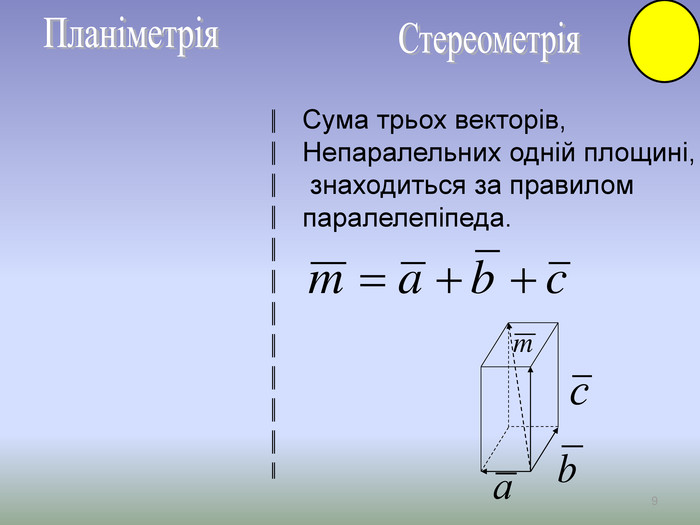
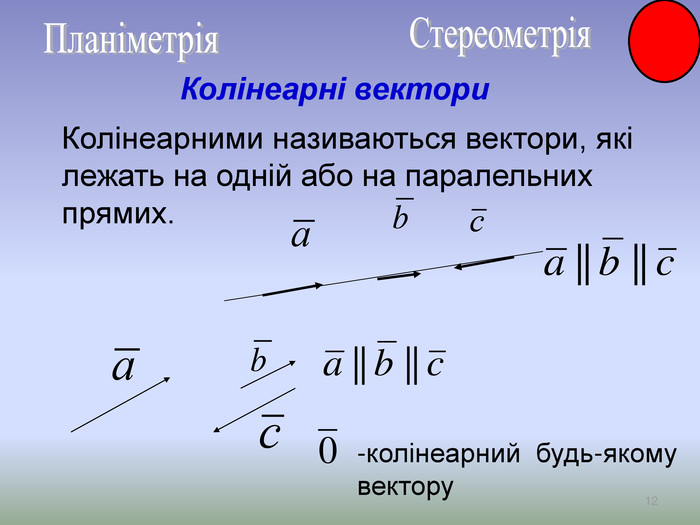
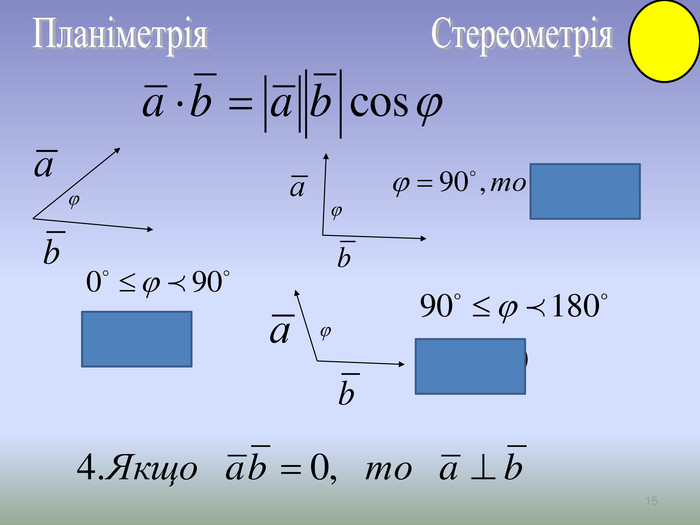
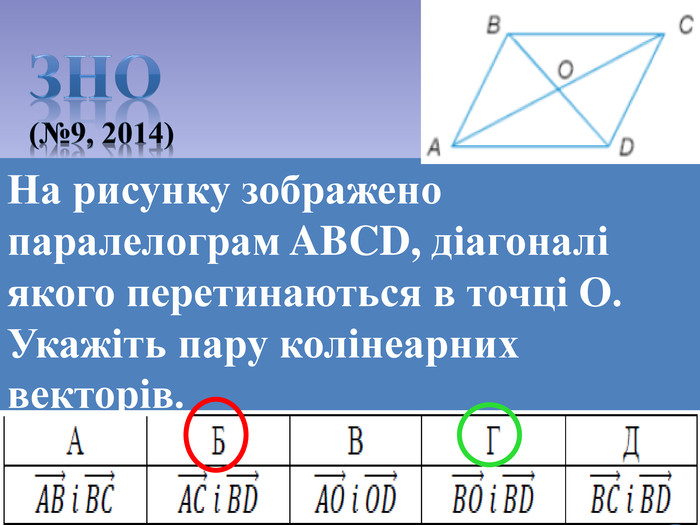
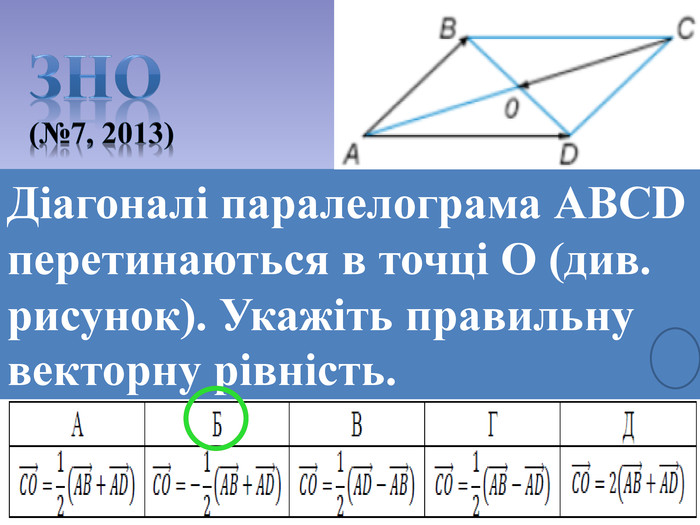
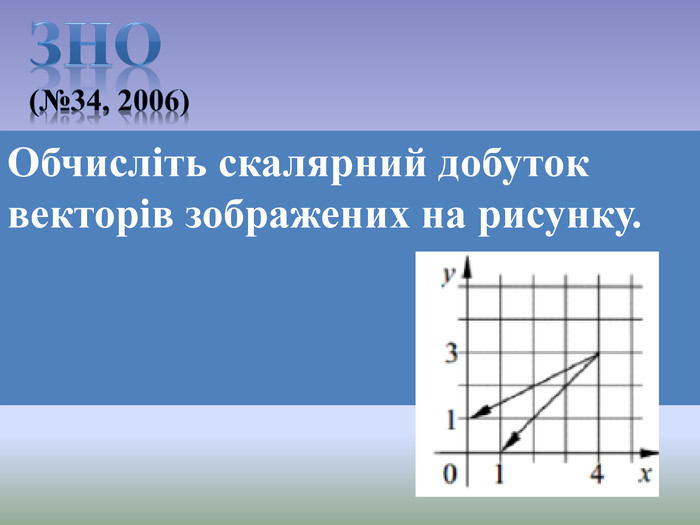
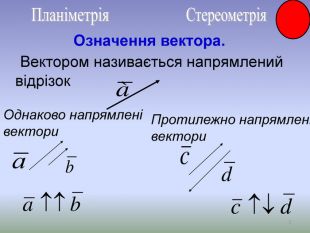
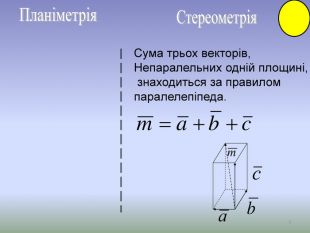
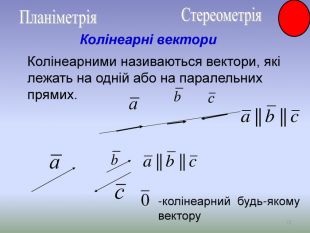
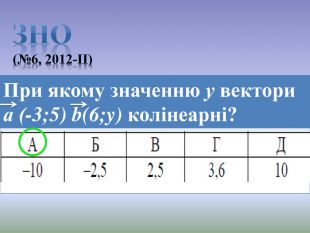
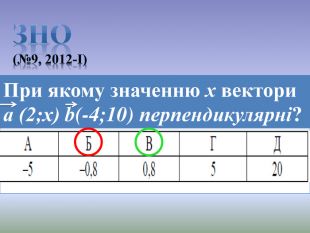
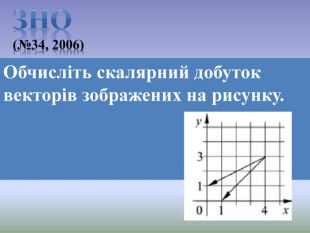
Презентація до уроку Вектори у просторі
Про матеріал
Презентація до уроку: Розв’язування задач
В даній презентації використовуються завдання ЗНО( різні роки)
Мета уроку:
Навчальна: узагальнити та систематизувати знання і вміння учнів з теми «Вектори у просторі»; перевірити рівень засвоєння знань учнів з теми, вміння користуватися вивченим матеріалом.
Розвиваюча: розвивати пам’ять, вміння виділяти головне, швидко орієнтуватися в різних ситуаціях.
Виховна: виховувати інтерес до предмету, наполегливість у досягненні мети, дисциплінованість, вміння раціонально використовувати час уроку.
Тип уроку: узагальнення та систематизація вивченого матеріалу
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку