Презентація на тему:"Конфігурації Трикутник - коло"
Про матеріал
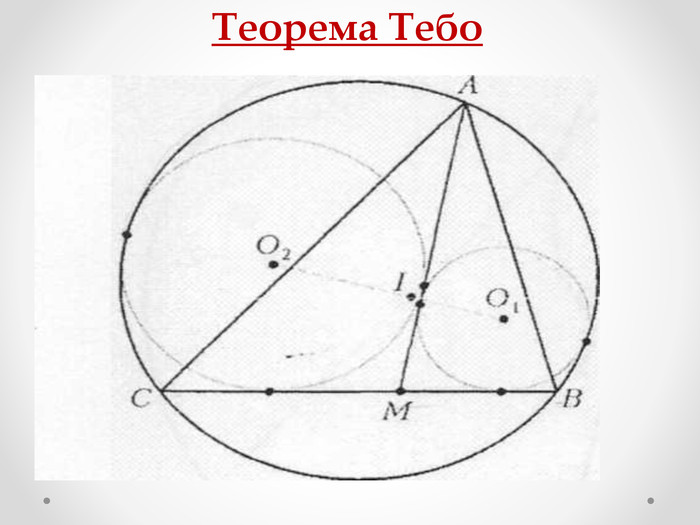
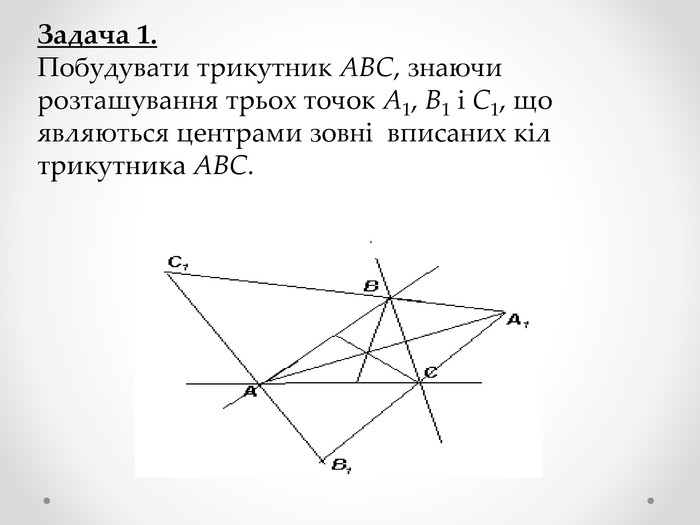
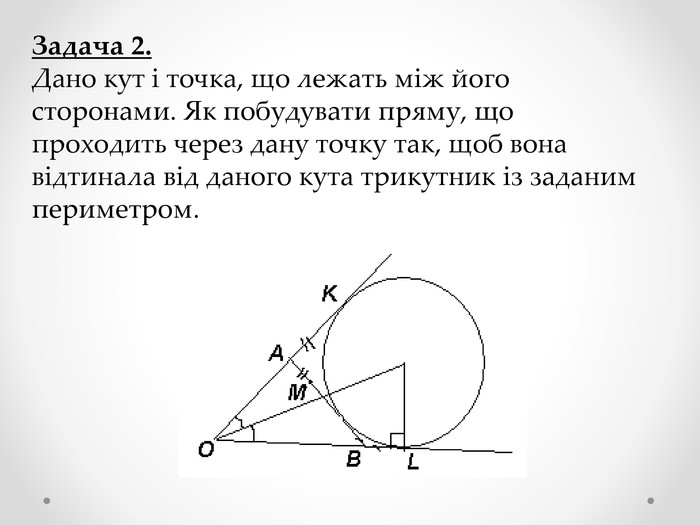
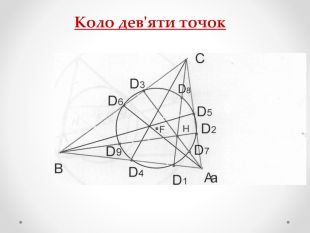
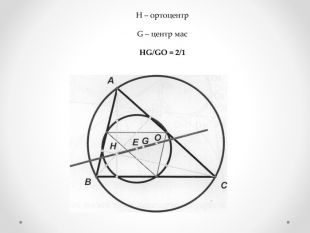
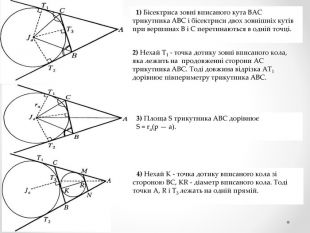
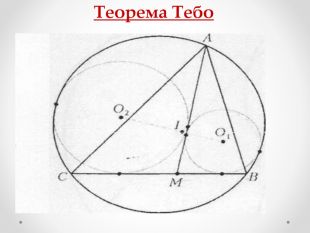
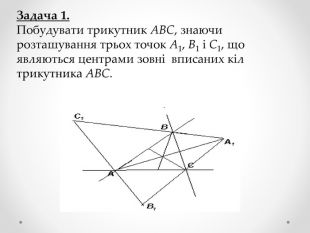
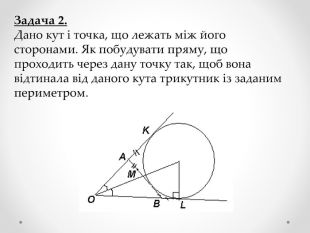
Мета роботи - застосування теорем Тебо та Фейєрбаха та їх наслідків до розв’язування задач та складання програми для знаходження центрів кіл та побудови вписаного, описаного, зовні вписаного кіл та кола Ейлера.
Перегляд файлу
Зміст слайдів
pptx
До підручника
Геометрія (академічний, профільний рівень) 11 клас (Бевз Г.П., Бевз В.Г., Владімірова Н.Г., Владіміров В.М.)
Оцінка розробки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку