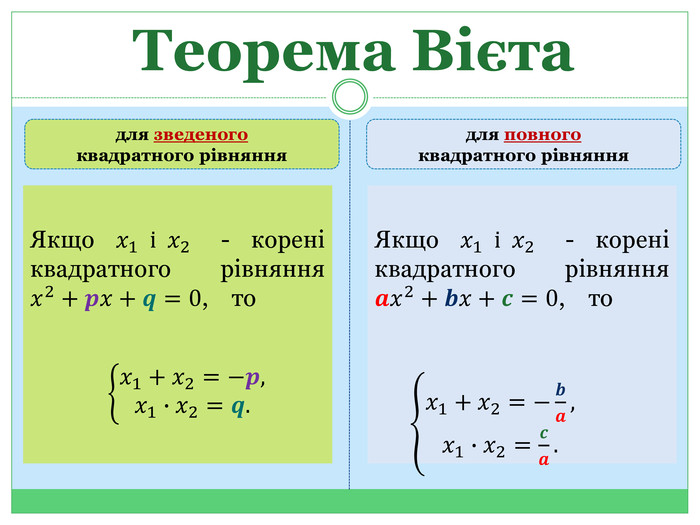
Теорема Вієта та теорема, обернена до теореми Вієта
Про матеріал
Перезентація до уроку алгебри у 8 класі з теми "Теорема Вієта". Мета уроку: домогтися засвоєння теореми Вієта і теореми, оберненої до теореми Вієта. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку