Презентація до уроку: "Вписані та описані кола (продовження)"
Про матеріал
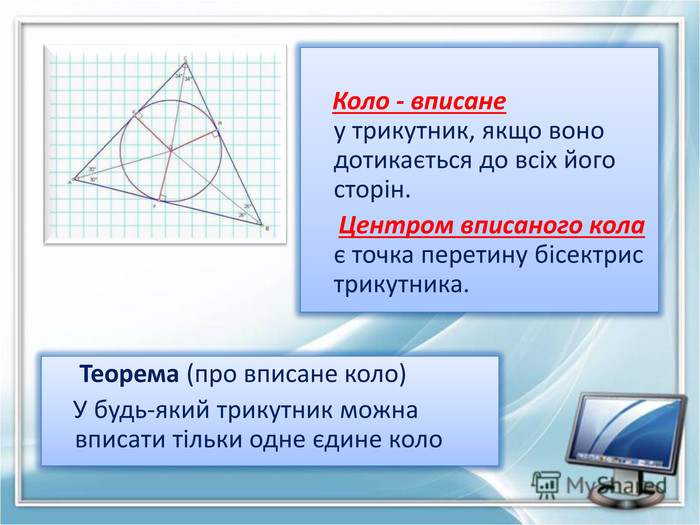
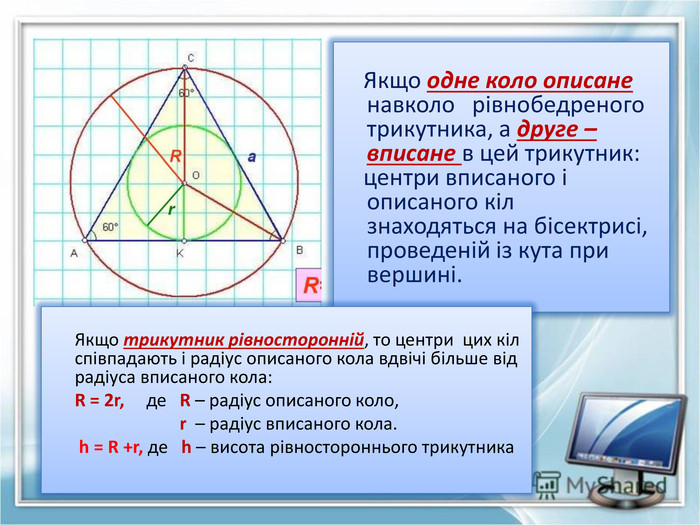
Матеріал уроку надає можливість ознайомитись з властивостями прямокутного і рівностороннього трикутника при вписуванні в них та описуванні навколо цих трикутників кіл Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку