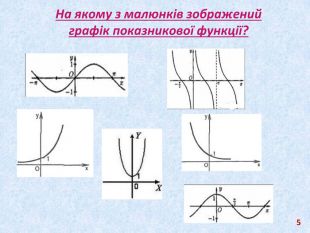
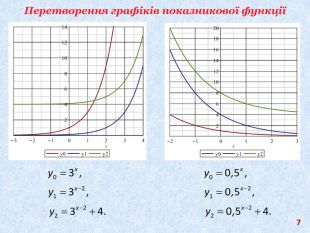
Презентація до уроку з алгебри в 11 класі з теми: «Показникова функція. Показникові рівняння та нерівності»
Про матеріал
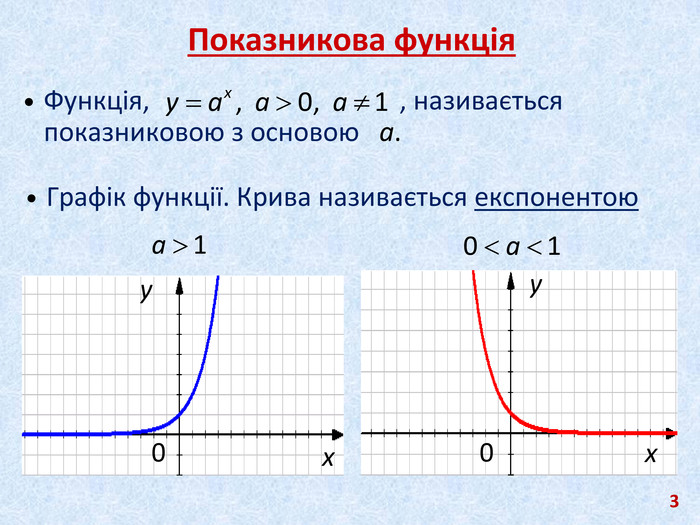
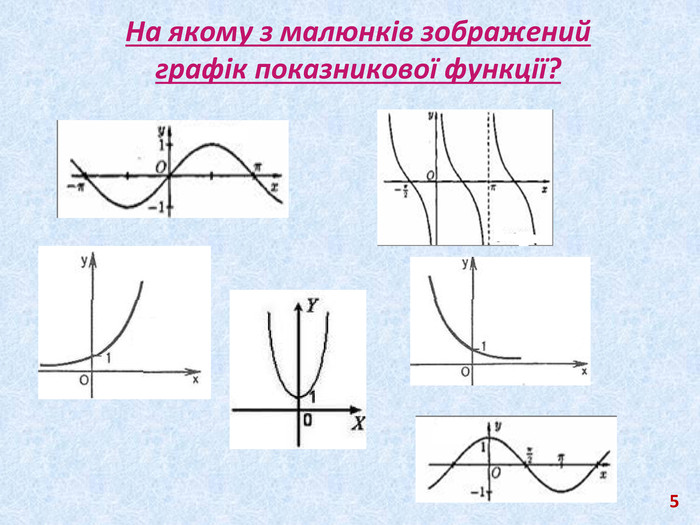
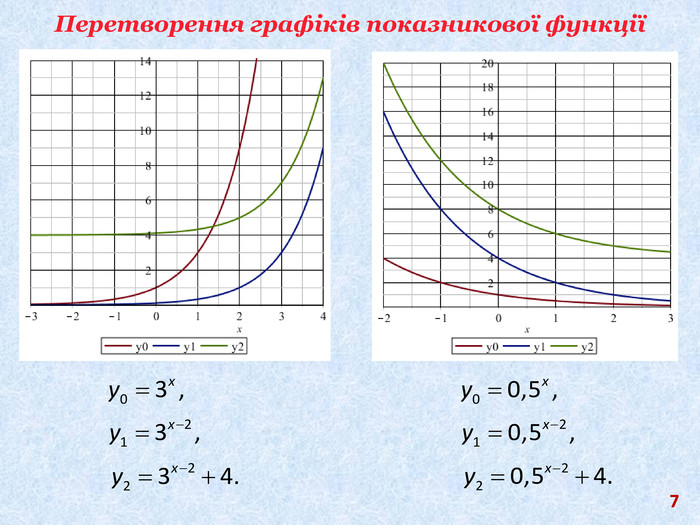
Презентація містить матеріал підібраний з метою систематизації та узагальнення знань по властивостях показникової функції, застосуванню її властивостей, а саме і до розв'язування показникових рівнянь та показникових нерівностей; для підготовки до контрольної роботи та ЗНО.
До підручника Алгебра (академічний рівень, профільний рівень) 11клас (А. Г. Мерзляк, Д. А. Номіровський, В. Б. Полонський, М. С. Якір
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку