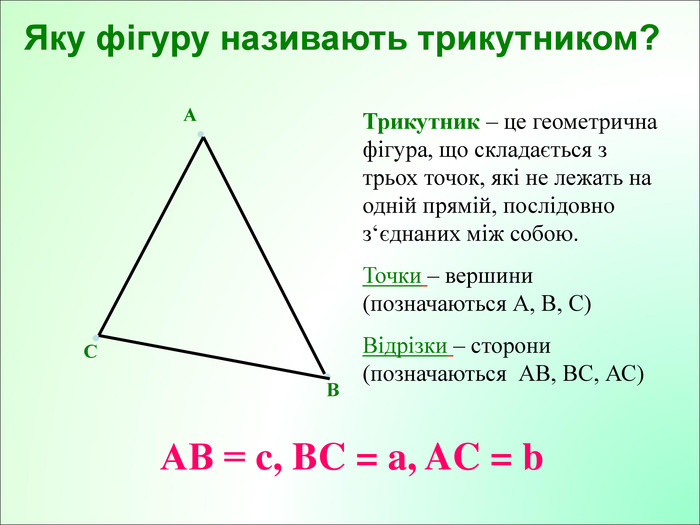
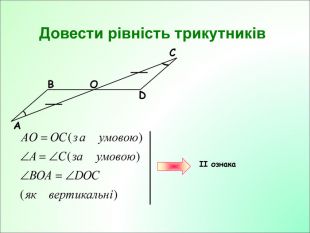
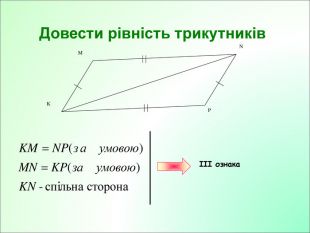
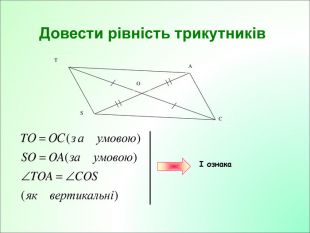
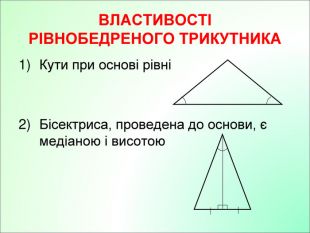
Презентація до уроку з геометрії у 7класі на тему"Рівнобндрений трикутник."
Про матеріал
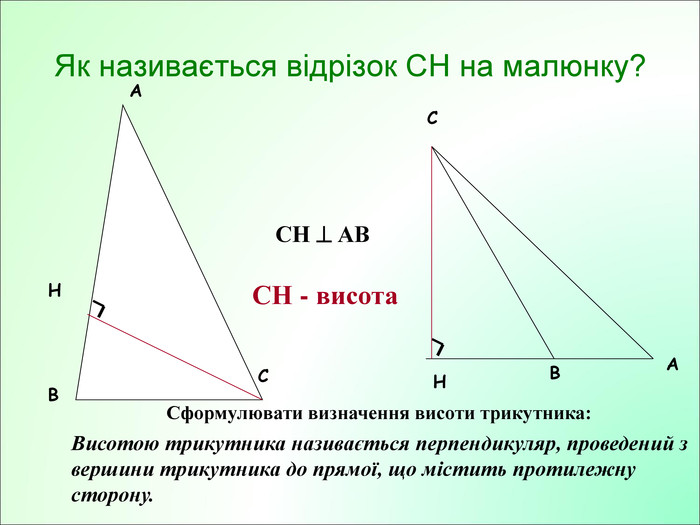
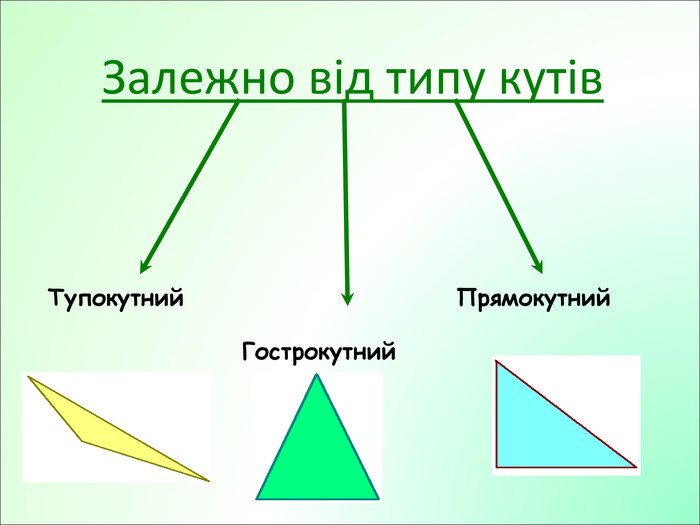
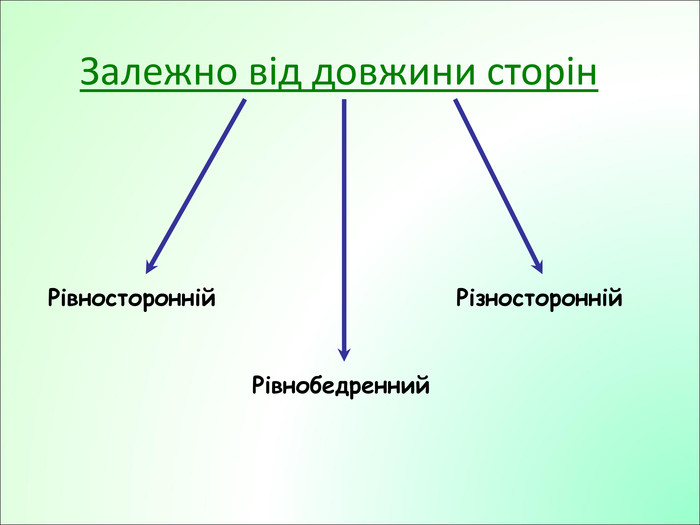
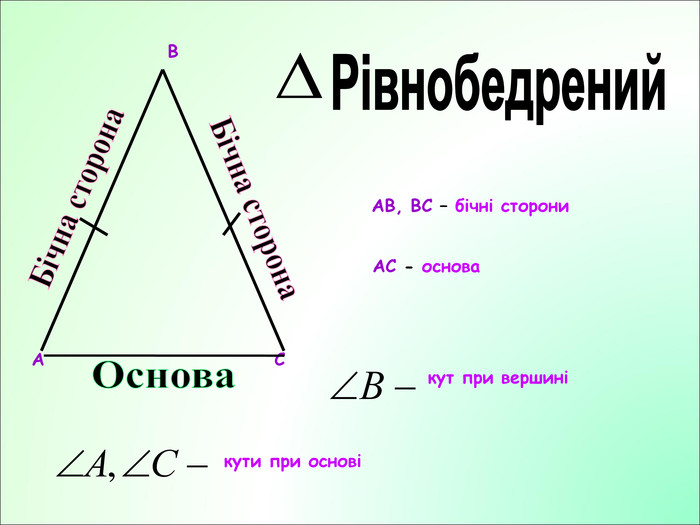
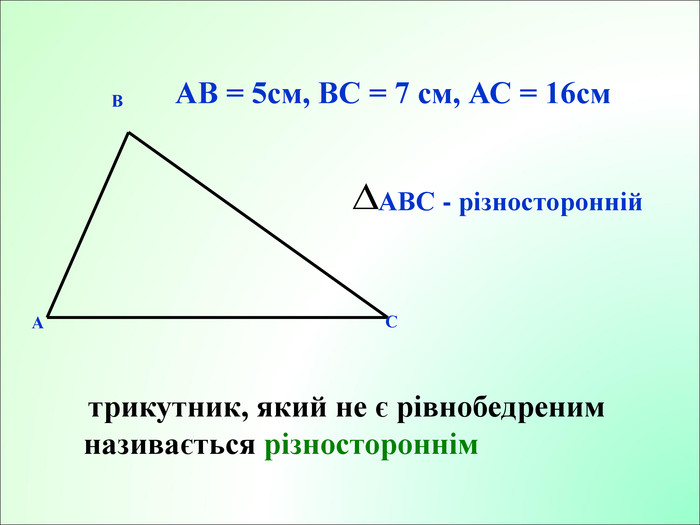
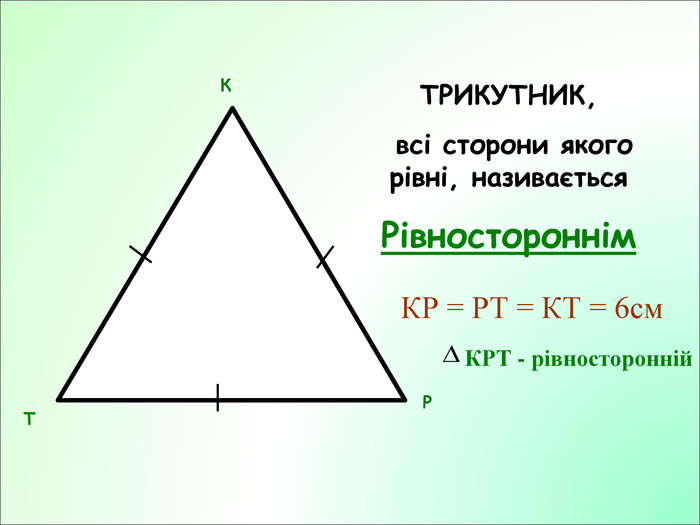
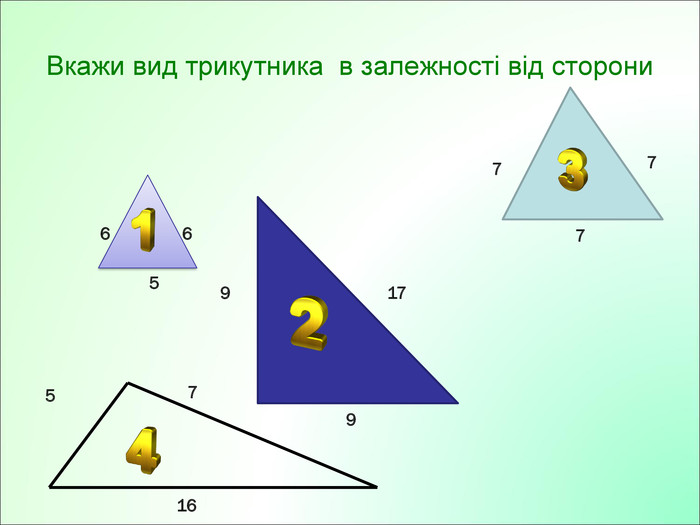
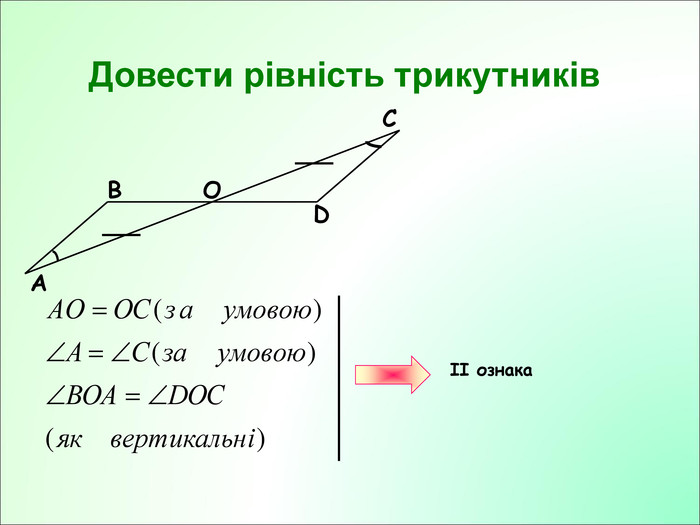
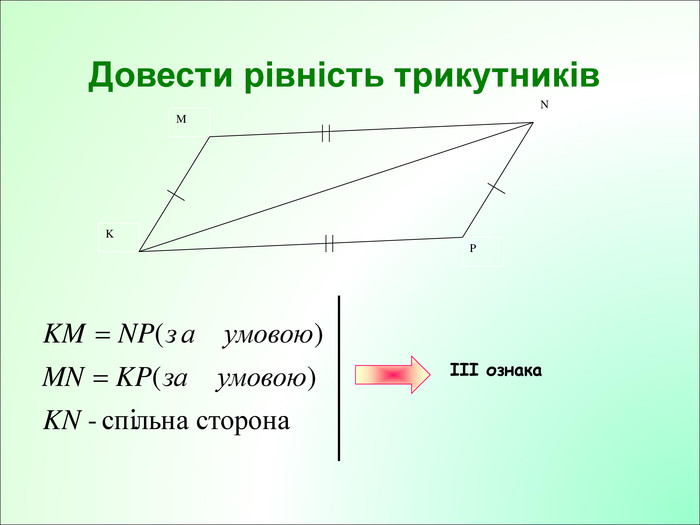
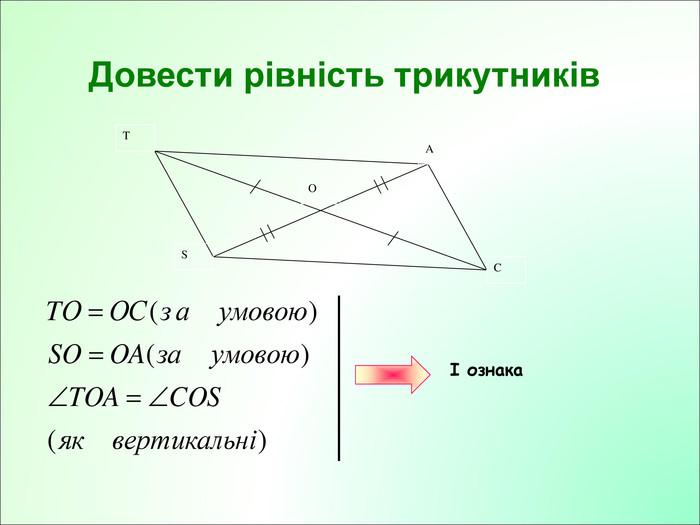
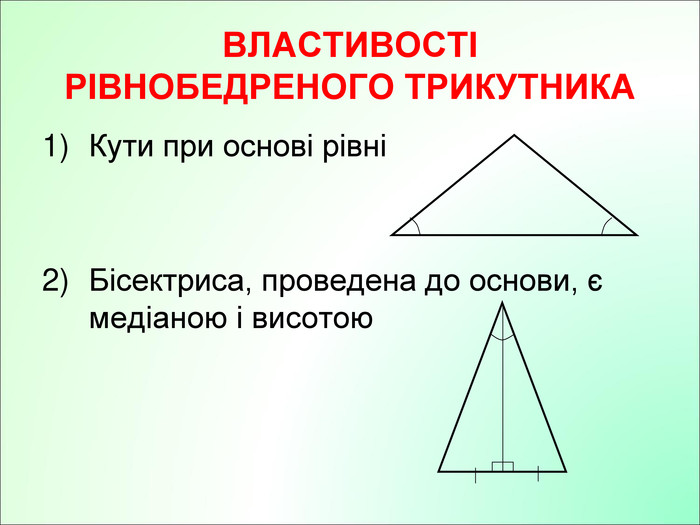
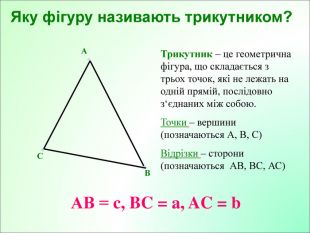
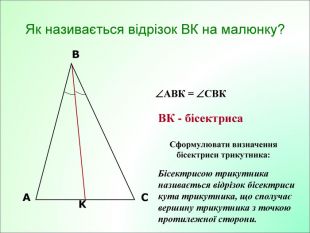
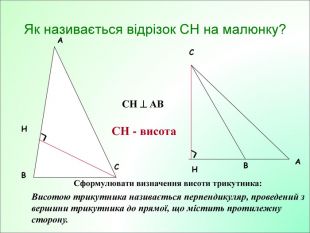
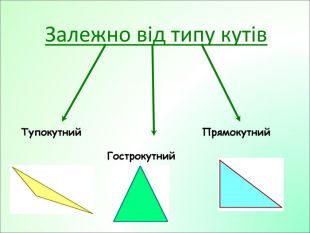
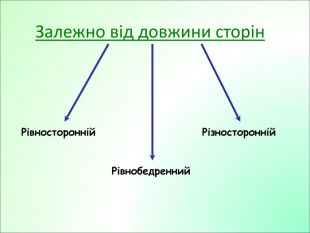
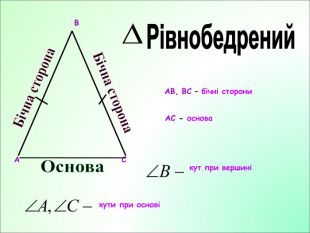
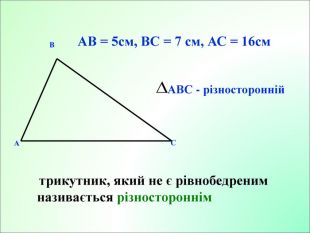
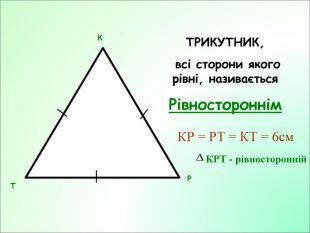
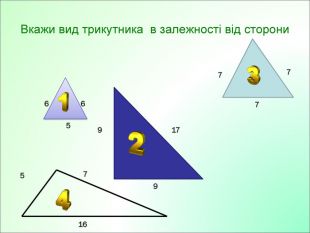
Презентація до уроку з геометрії у 7класі на тему"Рівнобедрений трикутник" складається з 29 слайдів. Ця презентація використовується на всіх етапах уроку, містить цікаві завдання і різні форми роботи. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
-
На Підсумковий урок саме то!
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку