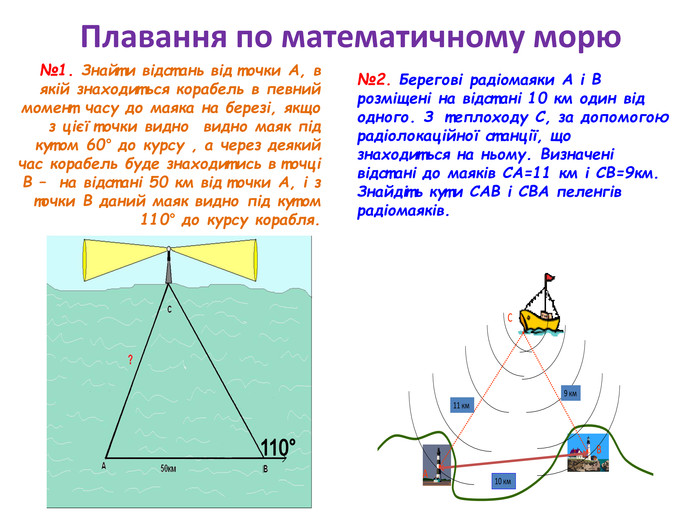
Презентація до уроку з геометрії у 9 класі на тему"Розв’язування трикутників."
Про матеріал
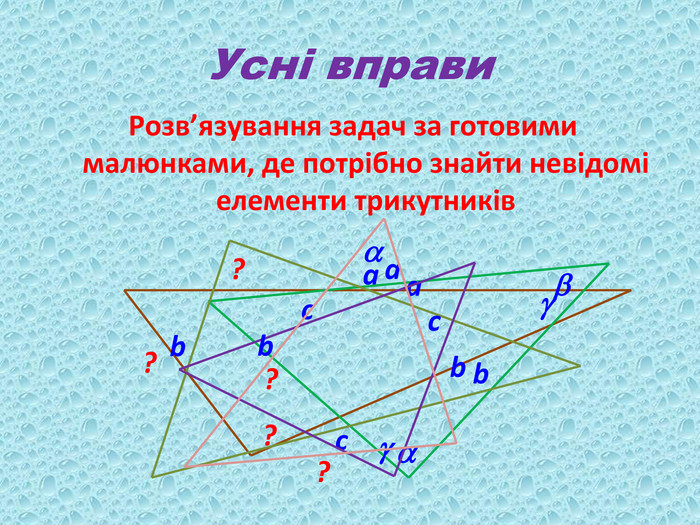
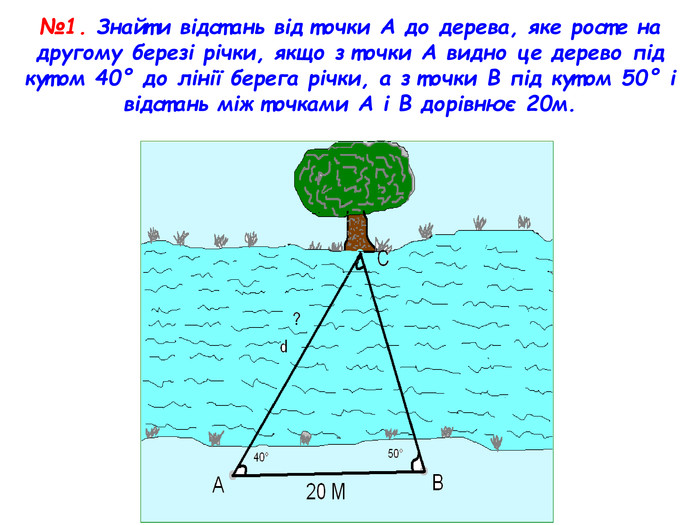
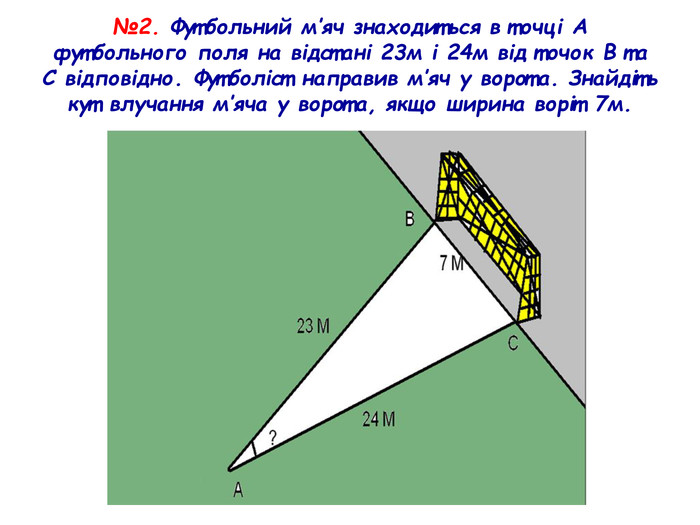
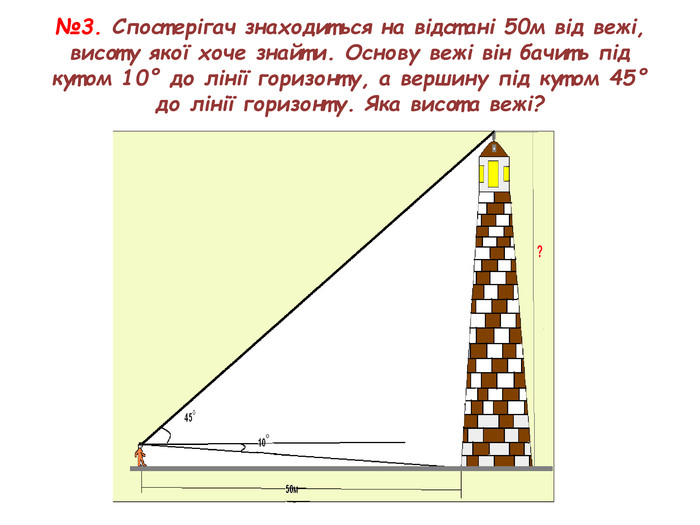
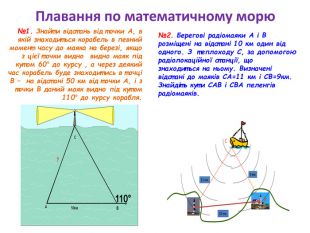
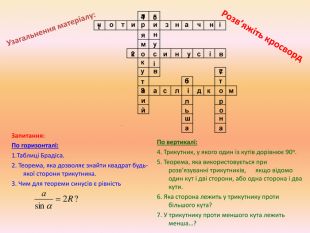
Презентація до уроку з геометрії у 9 класі на тему "Розв’язування трикутників" складається з 16 слайдів. Ця презентація використовується на всіх етапах уроку, містить цікаві завдання і різні форми роботи. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку