Розробка уроку геометрії для 9 класу на тему: "Розв'язування задач на обчислення площ трикутників ".

9 клас 

Тема уроку. Розв’язування задач на обчислення площ трикутників.

Мета уроку: удосконалити вміння розв’язувати задачі на обчислення площ трикутників за вивченими формулами; формувати навички розв’язувати прикладні задачі по темі з використанням елементів STEM-освіти (реальне застосування знань); розвивати логічне мислення, вміння робити висновки, встановлювати взаємозв’язки; виховувати уважність , самостійність,  позитивне ставлення до навчання.

Очікувані результати: учні повинні знати формули для обчислення площ трикутників і вміти їх застосовувати до розв’язування задач.

Компетентності, що формуються: математична – уміння застосовувати вивчені формули для обчислення площ трикутників; ключові -  інформаційно-цифрова (уміння страктувати дані, діяти за алгоритмом та складати план дій; визначати достатність даних для розв’язування задачі), уміння вчитися впродовж життя (уміння відбирати й застосовувати потрібні знання та способи діяльності); ініціативність і підприємливість (уміння аналізувати , прогнозувати, ухвалювати оптимальні рішення); соціальна і громадянська (уміння висловлювати власну думку, слухати і чути інших).

Обладнання: підручник, роздавальні матеріали, моделі трикутників.

Тип уроку: удосконалення знань і вмінь.        

Підручник. Бурда М.І. Геометрія: підруч. для 9 кл. загальноосвіт. навч. закл. / М. І. Бурда, Н. А. Тарасенкова. – К.: УОВЦ «Оріон»,2017.

     Хід уроку.

І. Забезпечення емоційної готовності.       

Усміхніться один одному і до вас  прийде радісний настрій. Будьте впевнені. Задоволені собою. А людина лише тоді може бути задоволена собою, коли досягає успіху. Сподіваюся. В кінці уроку кожен із вас зможе сказати: «Мені це вдалося!».                                                                                                                 На попередньому уроці ми розглянули формули для обчислення площ різних трикутників, розглянули основні типи задач на знаходження площ трикутників.                                                                                    Сьогодні перед нами стоїть задача:                                                                                                                              - повторити все, що вивчили ;                                                                                                                                            - пригадати те, що забули;                                                                                                                                            - вміло застосувати  отримані знання до розв’язування задач на знаходження площ трикутників. Незважаючи на те, що у нас  попереду багато роботи, я сподіваюся. Що ми зможемо зберегти гарний настрій до кінця уроку, а якщо вдасться, то ще його й покращимо.

ІІ. Перевірка домашнього завдання.                     1.Виконання домашніх вправ перевіряється за зразком записаним на дошці. (Взаємоперевірка).                                                                                                                                            2.Тестове завдання.                                                                                                                                                           У завданнях а і б випишіть усі правильні відповіді.                                                                                                  а ) Яку із записаних нижче  формул  можна використати для обчислення площі:                                                        □ прямокутного трикутника;                                                                                                                                            □ рівностороннього трикутника;                                                                                                                              □ довільного трикутника?                                                                                                                              б ) Яку із записаних нижче формул можна використати для обчислення площі:                                                        □ паралелограма;                                                                                                                                                          □ ромба;                                                                                                                                                                        □ квадрата;                                                                                                                                                                        □ прямокутника?                                                                                                                                            1) S=а²; 2) S=d²Sin; 3) S=; 4) S= 5) S=pr; 6)S=r(2R+r); 7) S;  8) S= d₁d₂Sin. 9) S=авSin; 10) S=; 11) S=; 12) S=а²Sin; 13) S= 14) S=.

ІІ. Актуалізація опорних знань і навиків учнів.                    1.Яка з фігур зайва і чому?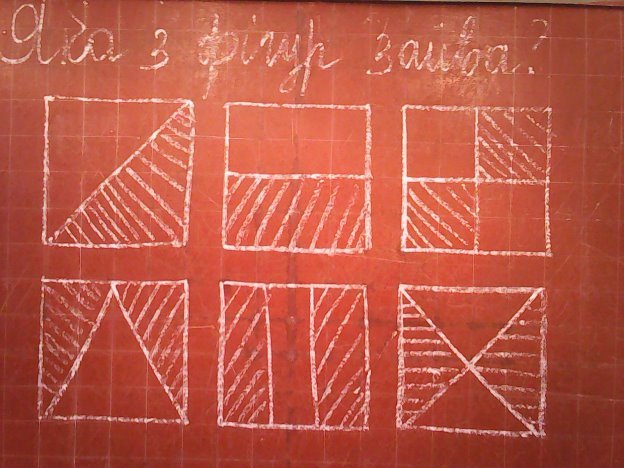

 2. При вимірюванні  площ земельних ділянок використовують різні одиниці вимірювання Що означає гектар, ар? Що означає сотка городу?                                                                                                                3. Вправа   «Відгадай формулу» (вчитель показує рисунок трикутника, а учні відгадують формулу за якою можна обчислити його площу). (Формули на початку виконання завдання закриті та поступово відкриваються з відповідями учнів).

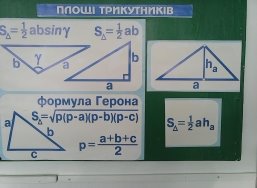
 ІІІ. Мотивація навчальної діяльності учнів.                    У шкільному підручнику з геометрії трикутнику приділяється значно більше уваги, ніж будь-якій іншій фігурі. Це пояснюється тим, що трикутник – дуже важлива фігура, багато властивостей якої мають велике практичне значення. А також вивчення властивостей багатьох інших геометричних фігур ґрунтується на знанні властивостей трикутника.                                                                       Трикутники мають важливе практичне і теоретичне значення.                                                                      (Виступи учнів з короткими повідомленнями про трикутник).                                                                      1. Основні властивості трикутника були відомі ще в стародавні часи. 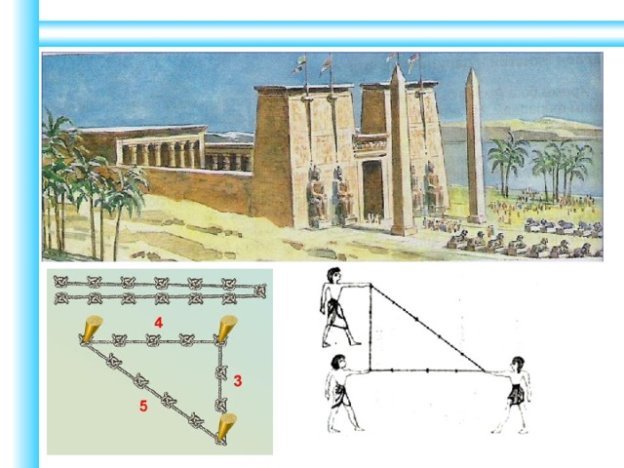Щоб споруди були міцними і стійкими, окремим їхнім деталям надають форми трикутника, тобто застосовують властивість трикутника, яка називається жорсткістю. Завдяки жорсткості трикутника таку форму мають елементи майже кожної будівельної конструкції: хвіртка, ворота, стріла крана. Стовпи високовольтної лінії, мостові ферми, телевізійні вежі. Кронштейн, ватерпас тощо.                 2. Площі деяких многокутників учені Єгипту вміли визначати ще за кілька тисячоліть до нашої ери. Життя змушувало це робити. Річка Ніл, розливаючись, щоразу змивала межі полів, і землеміри,знов і знов відновлювали їх.                                                                                                                                                                                                                                                                                                                       Кожний многокутник  можна розбити на трикутники. Отже, розбиваючи фігуру на трикутники, можна легко знайти її площу як суму площ складених трикутників. Так і робили єгипетські землеміри, визначаючи площі ділянок після розливу річки Нілу, а знаходити площу трикутника єгиптяни вміли вже кілька тисячоліть тому.                                                                                                   Нині площі полів, пасовиськ та інших угідь вимірюють обліковці, бригадири, землеміри. Адже кожному треба знати, скільки гектарів зорано, закультивовано, засіяно, удобрено, оброблено, зібрано тощо.                                                                                                                                                          3. Вимірювати площі земельних ділянок доводиться також геодезистам, маркшейдерам, шляховикам, будівельникам; площі оброблювальних поверхонь – штукатурам, мулярам, паркетникам. Покрівельникам, а площі витрачених матеріалів – текстильникам, жерстяникам, склярам і багатьом іншим фахівцям.                                                                                                                                            4. Відомим є правило «золотого трикутника», яке використовують у торгівлі. Знайшовши в магазині потрібний товар, покупець, придбавши його, прямує до каси. Завдання продавця – змусити покупця затриматися в приміщенні магазину якомога довше. Для цього він (продавець) розташовує товар, який користується найбільшим попитом, у вершинах уявного трикутника (у різних кінцях магазину), а саме для того, щоб змусити покупця пройти весь периметр магазину. Чим більша площа трикутника між входом, касовим вузлом і товаром, тим більш вдалим можна назвати планування магазину і від цього збільшується об’єм продажів. 

ІІІ. Повідомлення теми та мети уроку. 

ІV. Застосування знань і вмінь на практиці.                    1. Розв’язування задач за готовим рисунком № 630.                                                                                    2. Розв’язування задачі  за вказаним планом на обчислення площі трикутника за трьома сторонами № 631.                                                                                                                                                                        3. Обчислення площі паралелограма № 647 (а).                                                                                                  4. Розв’язування практичних задач.                                                                                                                              ● Очислити площу даного трикутника будь-яким відомим способом, модель якого ви отримали, зробивши потрібні вимірювання.                                                                                                                               ● № 672.На малюнку зображено план ділянки у масштабі 1:1000. Скориставшись планом , знайдіть площу цієї ділянки.

 5. Розв’язування задач за допомогою моделювання.                    Я вирішила написати лист. Аркуш паперу у формі паралелограма я  зігнула посередині. Потім з’єднала середини сторін із протилежними вершинами. Текст я вирішила розмістити у зафарбованій частині листа. Яку частину площі листа я виділила для повідомлення ?  (Всі дії учні роблять на моделі паралелограма).                                                                                                                                                                                                                                                                                                                                                                                                                                                                                            Підказка. Скористатися тим. Що діагональ паралелограма розбиває його на чотири трикутники з рівними площами.                                                                                                                                            6. Запропонувати спосіб практичних  вимірювань та обчислення площі причілка даху приватного будинку, який має форму трикутника.(Діти пропонують свої ідеї та спосіб обчислення).

 ІV. Рефлексивно-оцінювальний етап.                    Вправа  «Мікрофон».                                                                                                                                                          - Що нового ви дізнались на уроці?                                                                                                                              - Чи цікаво було вам працювати?                                                                                                                              - Чи задоволені ви результатами своєї роботи?                                                                                                  - Чи можете ви з радістю сказати «Мені це вдалося!»?                                                                                    - Що ви можете запропонувати для  роботи на наступних уроках?                                                                      Виставлення і коментування оцінок.                                                                                                                Метод «Похвали себе сам».                                                                                                                                            Учні вказують на позитивні сторони своєї роботи.                                                                                                                                                                                                                                                                          V.  Повідомлення домашнього завдання.                                                                                    Повторити формули для обчислення площі трикутника та  теоретичний матеріал $14.  Розв’язати вправи № 660 (б), 661 (4),674.                                                                                                                Творче завдання. Виконати презентацію чи зробити фотографії на тему: «Трикутник у спорудах нашого селища». (Зробити фотографії споруд селища, де зустрічаються конструкції  трикутників).

 Використана література.

1. Бевз Г. П. Прикладна спрямованість шкільного курсу геометрії. Посіб. для вчите теля.// Математика, № 25-28, липень 1999.                                                                                                                                            2. Возняк Г. М. Геометрія навколо нас. 7-9 класи. / Г. М. Возняк, О. Г. Возняк. – Тернопіль: Навч. книга-Богдан, 2012.                                                                                                                                                          3. Голодюк Л. С. Властивості трикутників. – Х.: Вид. група «Основа», 2003.                                                        4. Васильєва Д. В. Збірник задач з математики. 5-9 класи: Наскрізні лінії компетентностей та їх реалізація./ Д. В. Васильєва, Н. І. Василюк. – К.: Видавничий дім «Освіта», 2017.                                                        5. Теоретичні та методичні засади реалізації нового Державного Стандарту освітньої галузі «Математика» у 9 класі. Уклад. О. Д. Рафальська. // Математика в школах України, № 19-21 (535-537) липень 2017.                                                                                                                                                                        6. Раухман А. С. Усні вправи з геометрії для 7-11 класів: Посіб. для вчителя./ А. С. Раухман, Я. Г. Сень. – К.: Рад. шк., 1989.                                                                                                                                                          7. Черватюк О. Г. Елементи цікавої математики на уроках математики. Посіб. для вчителів./ О. Г. Черватюк, Г. Д. Шиманська. – К.: Рад шк., 1968.