Презентація "Двогранний кут"
Про матеріал
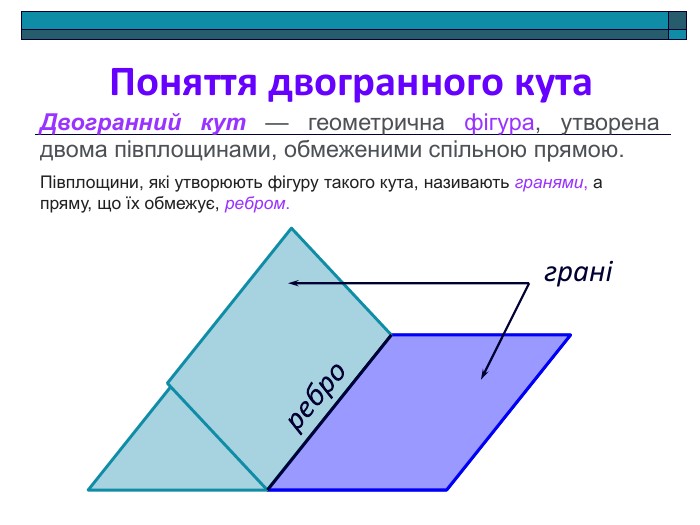
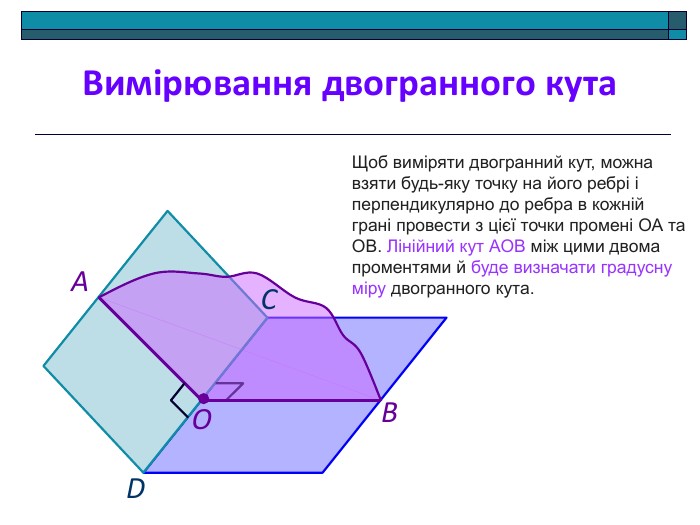
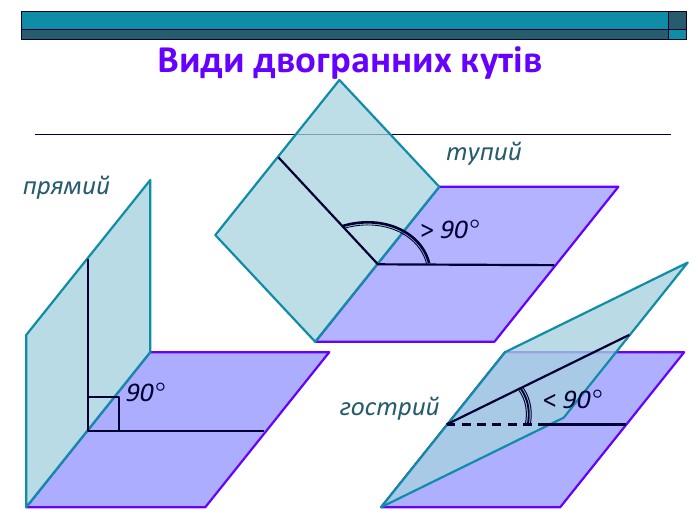
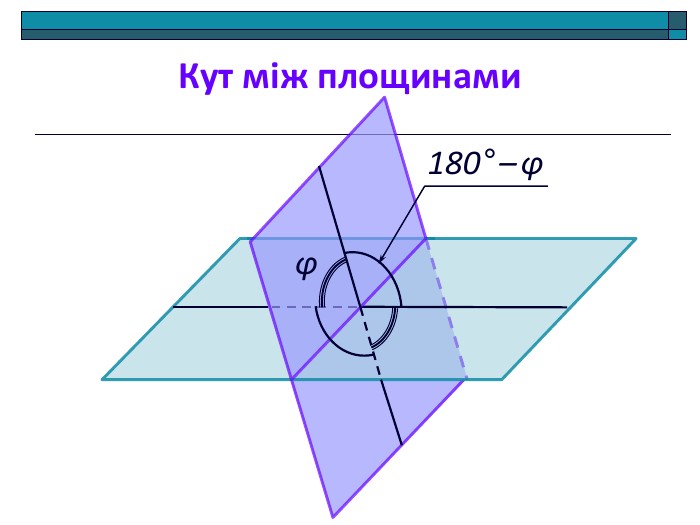
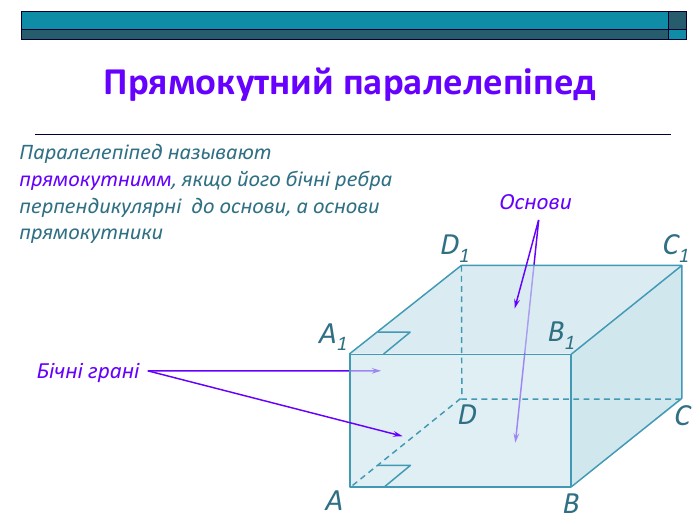
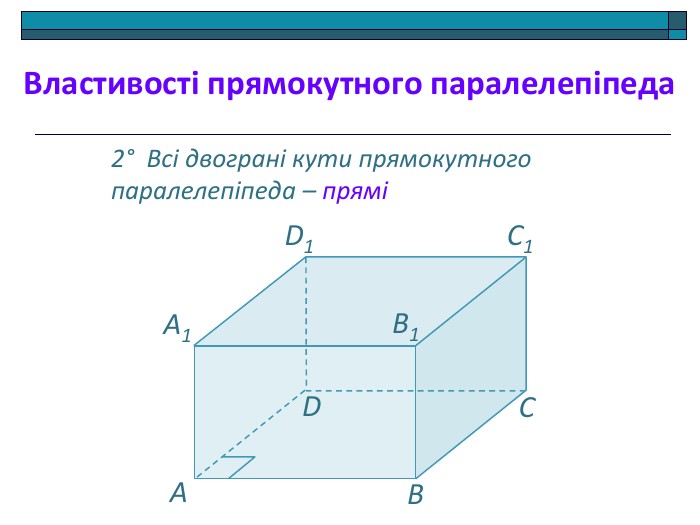
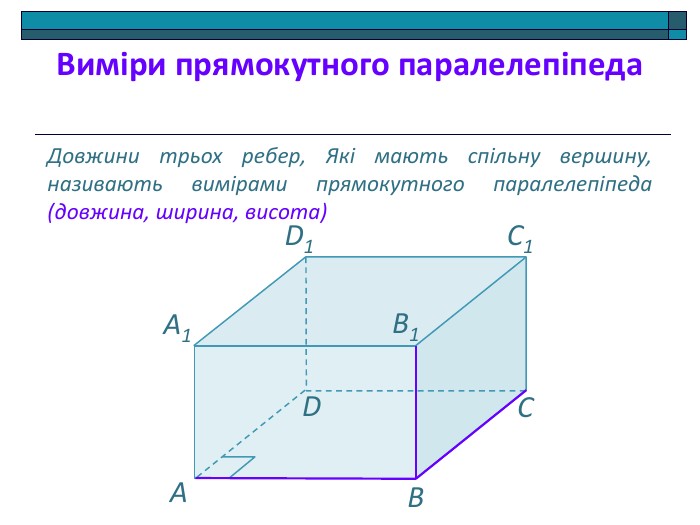
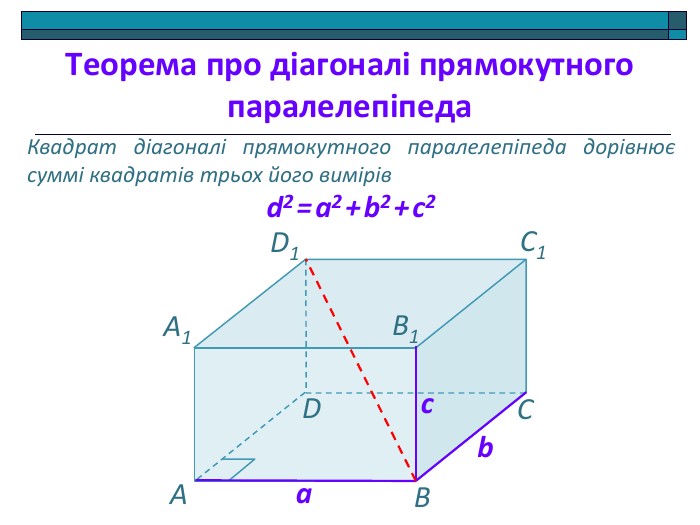
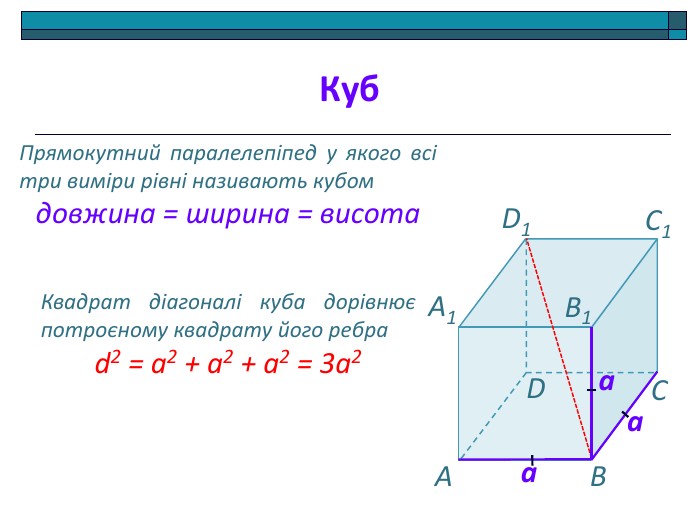
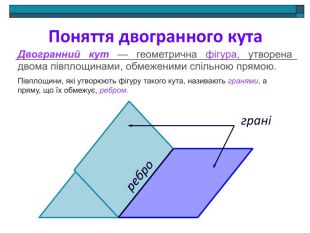
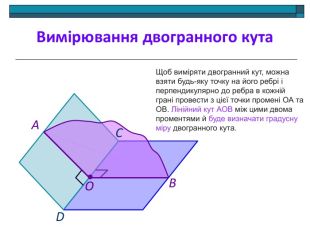
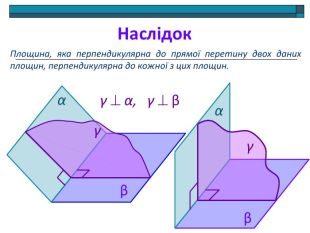
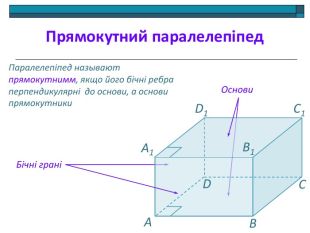
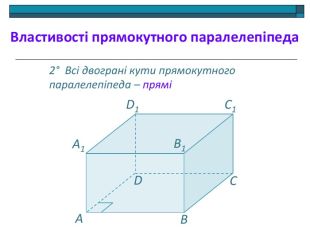
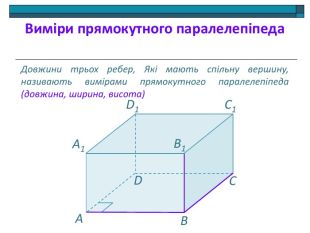
Анімована презентація: поняття двогранного кута, вимірювання двогранного кута, види двогранних кутів, прямокутний паралелепіпед, куб. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки

Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


























-

Крутько Світлана Олексіївна
20.01.2025 в 19:01
Дякую за змістовну презентацію!!!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Віннік Iрина Володимирівна
05.01.2025 в 22:46
Дякую за гарну роботу!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Клепікова Ольга Анатоліївна
12.12.2024 в 11:16
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Прудиус Елена
06.03.2024 в 19:04
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Румянцева Оксана Василівна
22.01.2024 в 18:29
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука