Презентація "Вектори у просторі"
Про матеріал
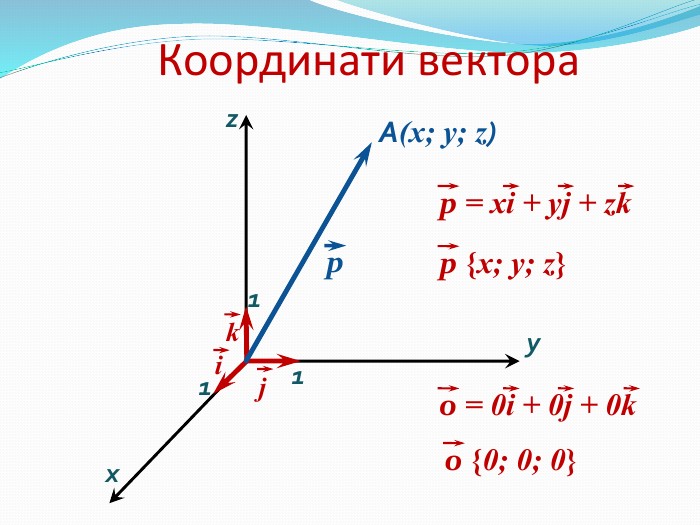
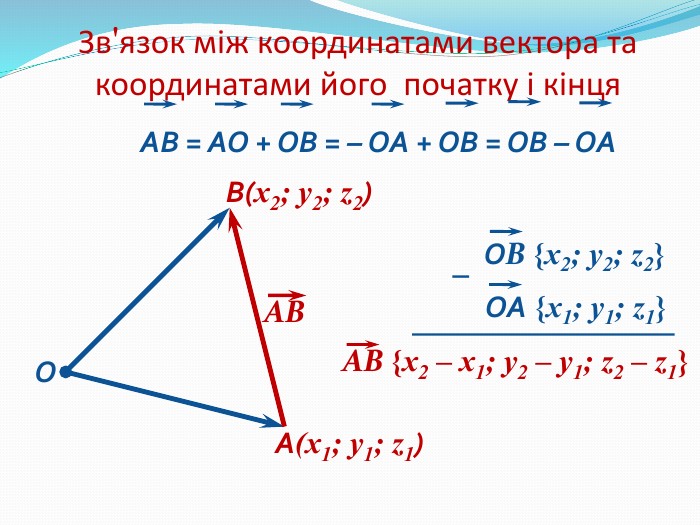
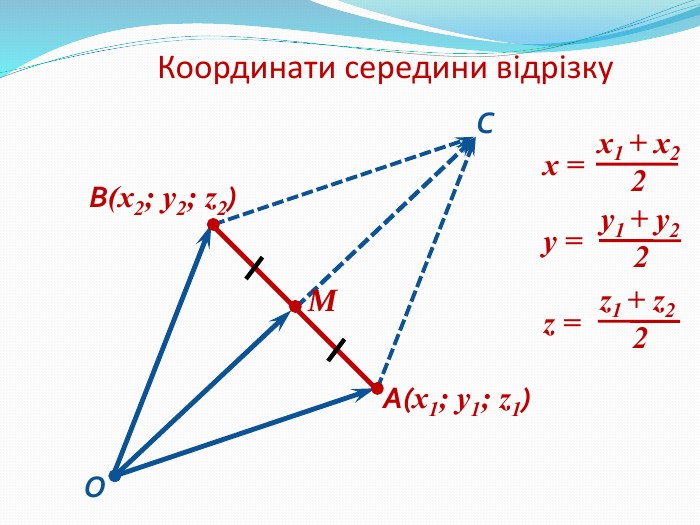
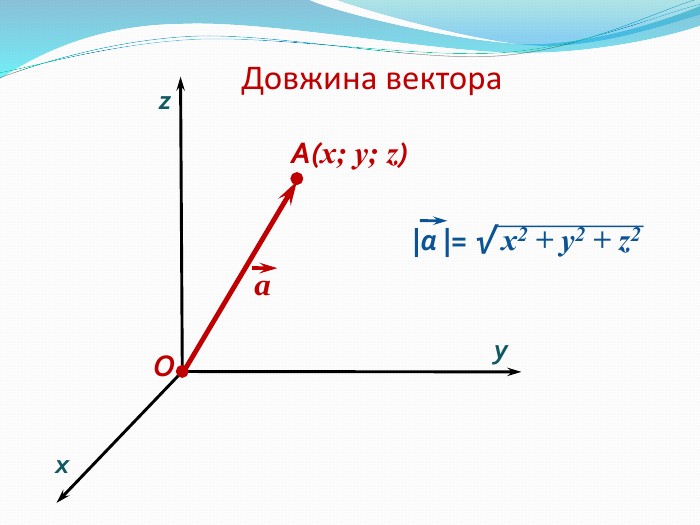
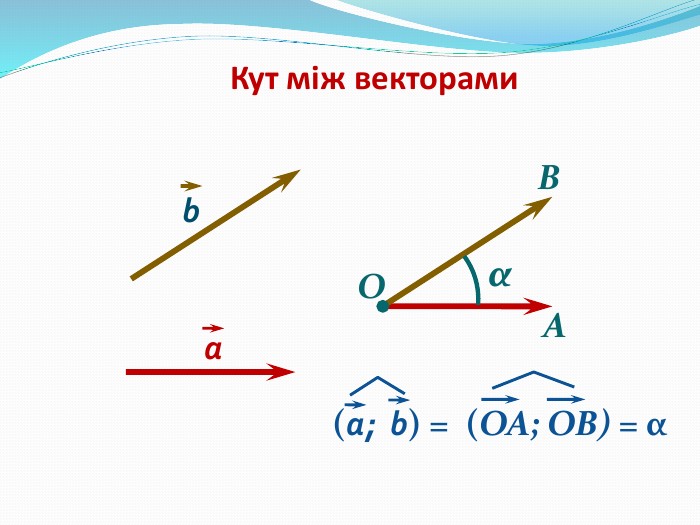
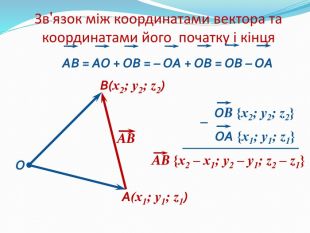
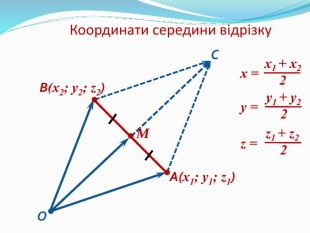
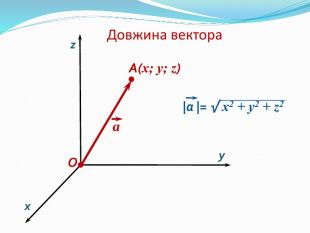
Анімована презентація: поняття вектора у просторі, основні формули з прикладами Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку