Презентація фізика 10клас І Частина "Кінематика"

Частина І “КІНЕМАТИКА”

Основна задача механіки. Абетка кінематики.

Механіка — це розділ фізики, в якому вивчаються механічні рухи матеріальних тіл, закони механічної взаємодії між ними та умови рівноваги тіл.

Механічним рухом називають зміну з часом положення тіла в просторі відносно інших тіл

Тіло, розмірами якого в умовах даного завдання можна знехтувати, називають матеріальною точкою

Відносність руху

Лінію, уздовж якого рухається тіло, називають траєкторією руху тіла

Переміщенням тіла називають спрямований відрізок, проведений з початкового положення тіла в його положення в даний момент часу

Швидкість руху. Середня і миттєва швидкості. Закони додавання переміщень і швидкостей

Швидкість руху Шви́дкість — фізична величинаа, що відповідає відношенню переміщення тіла до проміжку часу, за який це переміщення відбувалось. Швидкість — величина векторна, тобто вона має абсолютну величину і напрямок. У системі СІ швидкість (точніше її абсолютна величина) вимірюється в метрах за секунду — м/с. В системі СГС одиницею вимірювання швидкості є сантиметр за секунду — см/с. В повсякденному житті найпрактичнішою одиницею вимірювання швидкості є кілометр на годину — км/год. В певних областях людської діяльності чи країнах використовуються специфічні одиниці швидкості, як, наприклад, вузол чи фут за секунду.

Чим більше швидкість, тим більший шлях проходить тіло за одиницю часу. Якщо шлях вимірюється в метрах (м) і час руху в секундах (с), тоді швидкість тіла вимірюється в м/с.  Метр в секунду (м/с) — одиниця швидкості в Міжнародній системі одиниць. Швидкість можна виражати і в інших одиницях, наприклад, у (км/с) або в (км/год). Різні приклади швидкості:  1. Швидкість реактивного літака 3000 км/год; 2. Швидкість спринтера на дистанції 37 км/год; 3. Швидкість звуку в повітрі 1224 км/год; 4. Середня швидкість ходьби 6 км/год; 5. Максимальна швидкість гепарда 114 км/год; 6. Швидкість равлика 0,02 км/год.

Кінема́тика (від грец. κινειν — рухатись) у фізиці — розділ механіки, що вивчає способи опису руху матеріальних тіл без урахування їхньої маси, сил, які діють на них і причин виникнення руху. Окрім класичної, або ньютонівської кінематики, виокремлюють також релятивістську кінематику, яка вивчає способи опису рухів зі швидкостями, близькими до швидкості світла (див. Теорія відносності). Рух об'єктів мікросвіту (атомів, атомних ядер, елементарних частинок) описують методами квантової механіки.

Механічний рух – зміна з часом положення тіла або частин тіла в просторі відносно інших тіл. Тіло відносно якого розглядають рух усіх інших тіл про які йдеться в певній задачі називають тілом відліку. Щоб визначити положення тіла в просторі в даний момент часу , з тілом відліку повязують систему координат, яку задають за допомогою однієї або двох, трьох координатних осей. Розділ фізики, що вивчає закономірності механічного руху, називається механікою. Здебільшого під механікою розуміють класичну механіку, в якій вивчають рух макроскопічних тіл, що рухаються зі швидкостями, які в багато раз менші за швидкість світла у вакуумі. В основі класичної механіки лежать закони Ньютона. Тому її часто називають ньютонівською механікою. Закономірності руху тіл зі швидкістю близькою до швидкості світла у вакуумі вивчає релятивістська механіка, а закономірності руху мікрочастинок (наприклад: електронів, атомів, молекул, та інше) — квантова механіка. 

Середня і миттєва швидкості  У багатьох випадках нас цікавить не середня швидкість тіла за деякий проміжок часу, а швидкість тіла в даний момент часу, або миттєва швидкість. Для визначення миттєвої швидкості матеріальної точки слід прийняти до уваги те, що миттєва швидкість змінюється неперервно. Тому чим менше проміжок часу, протягом якого відбувається вимір переміщення, тим менше встигне змінитися середня швидкість і тим ближчою буде середня швидкість до її миттєвого значення. Виходячи з вище сказаного, можна визначити миттєву швидкість таким чином. Нехай в деякий момент часу  радіус-вектор, що характеризує положення тіла у просторі, дорівнює  (див. рис. 2.1). У момент часу  радіус-вектор буде , де  – переміщення за час . Тоді середня швидкість за цей проміжок часу буде дорівнювати

Середньою швидкістю руху за даний проміжок часу називається векторна величина, яка чисельно дорівнює відношенню вектора переміщення до проміжку часу, за яке це переміщення відбулось: Вимірюють середню швидкість у системі СІ у метрах за секунду (м/с). У багатьох випадках нас цікавить не середня швидкість тіла за деякий проміжок часу, а швидкість тіла в даний момент часу, або миттєва швидкість. Для визначення миттєвої швидкості матеріальної точки слід прийняти до уваги те, що миттєва швидкість змінюється неперервно. Тому чим менше проміжок часу, протягом якого відбувається вимір переміщення, тим менше встигне змінитися середня швидкість і тим ближчою буде середня швидкість до її миттєвого значення.

Тут корисно дати означення середньої швидкості нерівномірного руху: це гака швидкість, рухаючись з якою рівномірно, тіло той самий шлях пройде за той самий час, шо й при даному нерівномірному русі. З цього означення випливає геометричне тлумачення середньої швидкості: площа прямокутника під графіком швидкості рівномірного руху, шо дорівтос середній швидкості нерівномірного руху, повинна дорівнювати площі фігури під ірафікамн швидкостей при нерівномірному русі. Коли ми говоримо про швидкість руху різних тіл у навколишньому світі, то насамперед маємо на увазі середню швидкість. Саме вона дає змогу оцінити пройдений шлях, знаючи час руху, або навпаки, знайте час, знаючи відстань. Наприклад, вирушаючи на вокзал з іншого кінця міста, ми розраховуємо свій час. виходячи з відомої (з власного досвіду) середньої швидкості руху міського транспорту. При цьому ювсім не мас значення, як змінюються миттєва швидкість автобуса між зупинками. Для визначення середньої швидкості ми подумки замінюємо істинний складний нерівномірний рух на деякий простий рівномірний рух, при якому тіло проходить той самий шлях.Існують два різних поняття середньої швидкості: векторна середня швидкість., яка обчислюється за вектором переміщення тіла у певний проміжок часу. Скалярна середня швидкість, що обчислюється за шляхом, пройденим тілом уздовж траєкторії

Закони додавання і переміщень швидкостей. Швидкості руху тіла в різних системах відліку пов’язує між собою класичний закон додавання швидкостей. Швидкість тіла відносно нерухомої системи відліку дорівнює сумі швидкостей тіла рухомій системі відліку і самої рухомої системи відліку відносно нерухомої. Наприклад, пасажирський поїзд рухається по залізниці зі швидкістю 60 км/год. По вагону цього поїзда йде людина зі швидкістю 5 км/ч. Якщо вважати залізну дорогу нерухомої і прийняти її за систему відліку, то швидкість людини відносно системи відліку (тобто щодо залізниці), буде дорівнює складання швидкостей поїзда і людини, тобто60 + 5 = 65, якщо людина йде в тому ж напрямку, що і поїзд60 – 5 = 55, якщо людина і поїзд рухаються в різних напрямках. Однак це справедливо тільки в тому випадку, якщо людина і поїзд рухаються по одній лінії. Якщо ж людина буде рухатися під кутом, то доведеться враховувати цей кут, згадавши про те, що швидкість – це векторна величина.

А тепер розгляньмо описаний вище приклад більш детально – з деталями і картинками. Отже, в нашому випадку залізниця – це нерухома система відліку. Поїзд, який рухається по цій дорозі – це рухома система відліку. Вагон, яким іде людина, яка є частиною поїзда. Швидкість людини відносно вагона (відносно рухомої системи відліку) дорівнює 5 км/год. Позначимо її літерою  Ч. Швидкість поїзда (а значить і вагона) відносно нерухомої системи відліку (тобто щодо залізниці) дорівнює 60 км/ч. Позначимо її літерою  B. Інакше кажучи, швидкість потяга – це швидкість рухомої системи відліку відносно нерухомої системи відліку.

Пасажир, який сидить у поїзді, котрий рухається зі швидкістю 20 м/с, вважає себе нерухомим, а спостерігач на станції скаже, що поїзд, а з ним пасажир, промчали із швидкістю поїзда 20 м/с. Якщо пасажир буде рухатись у поїзді вздовж коридорі за рухом поїзда із швидкістю 1 м/с, то його швидкість відносно пасажира на станції вже буде 20 + 1 = 21 м/с, тому, що він здійснив переміщення. S¯=S1¯+S2¯.

Рівноприскорений прямолінійних рух. Прискорення

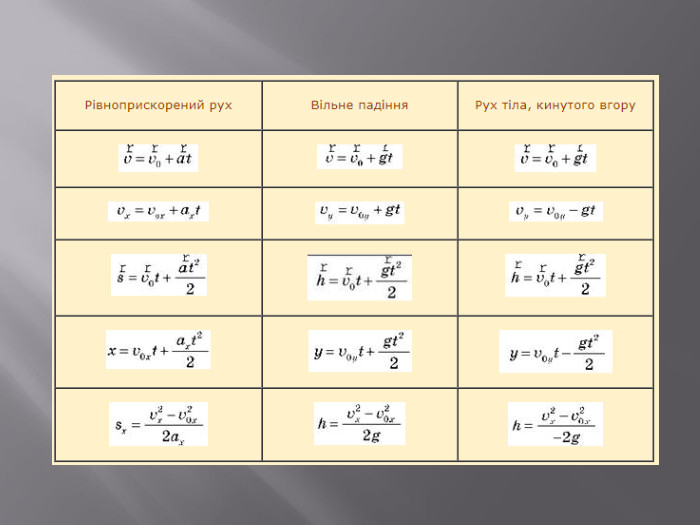
Рівноприскорений рух — найпростіший вид механічного руху, при якому прискорення залишається сталим. Частковим випадком рівноприскореного руху є рівносповільнений рух, який відбувається тоді, коли напрямки початкової швидкості і прискорення протилежні. Прикладом рівноприскореного руху може бути рух тіла в полі сталого земного тяжіння при умовах, коли опором повітря можна знехтувати.

Рівноприскореним прямолінійним рухом матеріальної точки називається рух, під час якого за будь-які рівні проміжки часу її швидкість змінюється однаково, тобто це рух з  . Для розв’язування задач корисно пам’ятати три рівняння кінематики рівноприскореного прямолінійного руху:1)  ;2)  ;3)  . У цих рівняннях початкові значення величин позначаються індексом «0» (нуль), а кінцеві значення записуються без індексу.

ПРИСКОРЕННЯ Приско́рення — векторна фізична величина, похідна швидкості по часу і за величиною дорівнює зміні швидкості тіла за одиницю часу. Прискорення, як векторна величина здебільшого позначається літерою «а»,а коли йдеться лише про кількісне значення прискорення  — a (від лат. acceleratio — прискорення). Часто у фізиці для позначення прискорення використовують дві крапки над позначенням  координати чи радіуса-вектора, або одну крапку над символом швидкості:

Рух тіла, при якому його прискорення не змінюється (ні за величиною, ні за напрямком), називається рівноприскореним рухом. У фізиці термін прискорення використовується і в тих випадках, коли швидкість тіла за модулем не збільшується, а зменшується, тобто тіло сповільнюється. При сповільненні вектор прискорення направлений проти руху, тобто протилежний до вектора швидкості. Прискорення — одне з базових понять класичної механіки. Воно поєднує між собою кінематику й динаміку. Знаючи прискорення, а також початкові положення й швидкості тіл, можна передбачити, як тіла будуть рухатися надалі. З іншого боку, значення прискорення визначається законами динаміки через сили, що діють на тіла.

Прискорення — векторна величина. Його напрямок не завжди збігається із напрямком швидкості. В загальному випадку вектор прискорення утворює з вектором швидкості деякий кут і розкладається на дві складові. Складова вектора прискорення, яка направлена паралельно до вектора швидкості, а отже, вздовж дотичної до траєкторії, називається тангенціальним прискоренням. Складова вектора прискорення, що направлена перпендикулярно до вектора швидкості, а отже, вздовж нормалі до траєкторії, називається нормальним прискоренням.

Вільне падіння і криволінійний рух під дією незмінної сили тяжіння

Вільне падіння. Попри слово падіння в назві, під дією сили тяжіння тіло не обов'язково повинно рухатися вниз. До прикладів вільного падіння належать рух тіла, підкинутого вертикально вгору або під кутом до горизонту, обертання Землі навколо Сонця тощо. Особливістю вільного падіння є те, що рух тіла не залежить від його маси, оскільки сила тяжіння пропорційна масі. Рівняння руху тіла у вільному падінні набирає вигляду: В умовах Землі поле тяжіння однорідне, і напруженість гравітаційного поля   дорівнює прискоренню вільного падіння. Однак необхідною умовою вільного падіння є можливість знехтувати опором повітря. У повітрі пір'їнка падатиме довше, ніж камінь. У повітрі на тіло діє сила Архімеда, тому тіла з густиною, меншою від густини повітря, не падатимуть, а підійматимуться вгору. Маленькі тіла, наприклад, частинки пилу або сніжинки, навіть маючи густину, більшу від густини повітря, падатимуть довго через броунівський рух.

У 1583 році італійський вчений Галілео Галілей (1564-1642) встановив, що при відсутності опору повітря всі тіла, незалежно від їх маси, падають на землю з однаковим прискоренням g, яке направлене вертикально вниз. Це прискорення називається прискорення вільного падіння. При вільному падінні тіла з невеликої висоти h від поверхні Землі (причому hьнабагатоменше радіуса Земліт. Rз, де радіус Землі Rз ~ 6000 км) сила тяжіння залишається практично постійною, тому прискорення вільного падіння також залишається постійним.

Вільне падіння можна розглядати як окремий випадок рівноприскореного руху. Прискорення вільного падіння залежить від висоти над рівнем моря і від географічної широти місця. Воно змінюється приблизно від 9,83 м/с2 на полюсі і до 9,78 м/с2 на екваторі. На широті Києва прискорення вільного падіння приймається рівним g = 9,8 м/с2. Тому в більшості випадків при рішенні задач з фізики прискорення вільного падіння приймається рівним 9,8 м/с2. Відмінність в значенні прискорення пояснюється добовим обертанням Землі і її формою – Земля сплюснута біля полюсів, тому полюсний радіус менше екваторіального радіуса.

У деяких районах земної кулі прискорення вільного падіння може відрізнятися від значення прискорення на даній широті. Такі відхилення спостерігаються в місцях, де є поклади корисних копалин. Рух тіл по вертикалі (вгору або вниз) поблизу поверхні Землі без урахування опору повітря є прямолінійним рівноприскореним рухом. При описі такого руху вибирають координатну вісь OY, спрямовану вгору або вниз. Незалежно від напрямку осі OY вектор прискорення вільного падіння спрямований вертикально вниз.

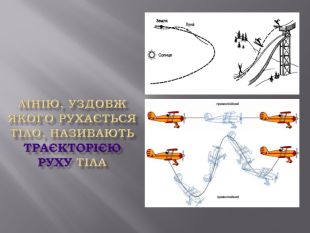
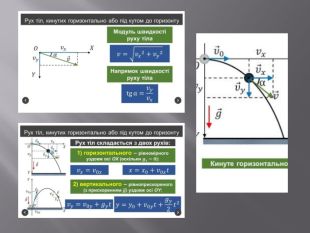
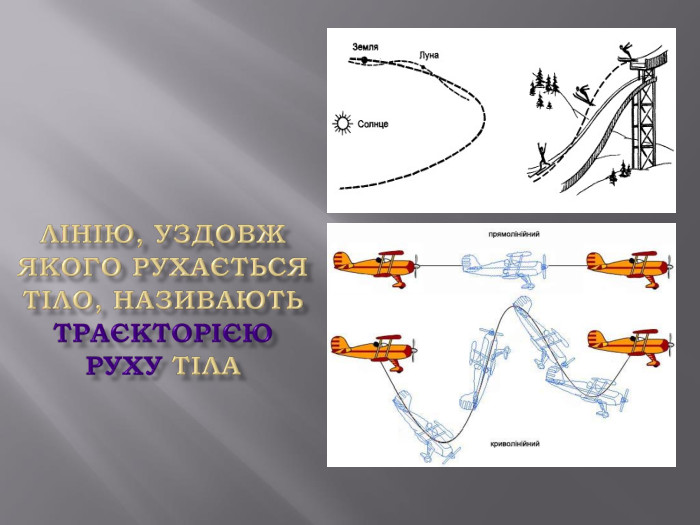
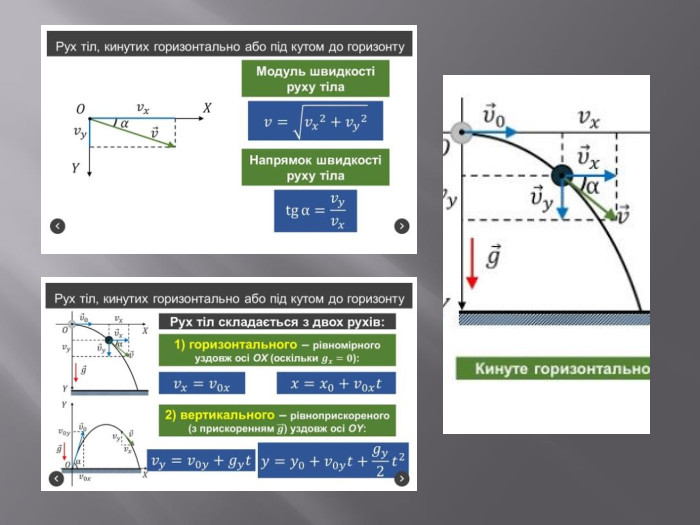
Криволінійний рух. Досі ми розглядали рухи, коли тіло переміщувалось уздовж прямої лінії. І в природі, і в техніці часто зустрічаються рухи, траєкторії яких є не прямими, а кривими лініями. Такі рухи називають криволінійними. І зустрічаються вони значно частіше, ніж прямолінійні. По криволінійних траєкторіях рухаються в космічному просторі планети і штучні супутники, а на Землі – води річок, повітря атмосфери, автомобілі і літаки, деталі машин і механізмів. Криволінійним є рух тіла, кинутого під кутом до горизонту, рух по колу. Завдання вивчення криволінійного руху, як і у випадку прямолінійного, полягає в тому, щоб за швидкістю тіла визначати його положення у будь-який момент часу. Складність полягає у тому, що вектор переміщення під час такого руху напрямлений не вздовж траєкторії, бо траєкторія у цьому випадку є кривою лінією. Напрям руху, тобто напрям вектора швидкості також увесь час змінюється; змінюється і вектор прискорення.

При криволінійному русі вектор швидкості завжди спрямований вздовж дотичної до траєкторії руху. Будь-який криволінійний рух можна представити у вигляді суми прямолінійних рухів і рухів по колах різних радіусів. Швидкість змінюється як за величиною, так і за напрямком. Вектор прискорення спрямований під кутом до вектора швидкості. Рівномірний рух точки колом є найпростішим щодо математичного опису виглядом криволінійного руху – це рух точки з постійною за модулем швидкістю (    = const) траєкторією, що представляє собою коло. Але, оскільки швидкість завжди спрямована вздовж дотичної до траєкторії руху, то за напрямком вона змінюється.

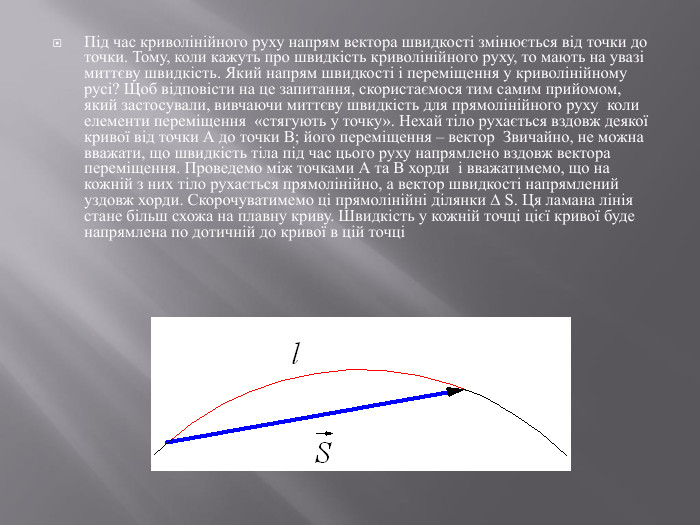
Під час криволінійного руху напрям вектора швидкості змінюється від точки до точки. Тому, коли кажуть про швидкість криволінійного руху, то мають на увазі миттєву швидкість. Який напрям швидкості і переміщення у криволінійному русі? Щоб відповісти на це запитання, скористаємося тим самим прийомом, який застосували, вивчаючи миттєву швидкість для прямолінійного руху  коли елементи переміщення  «стягують у точку». Нехай тіло рухається вздовж деякої кривої від точки А до точки В; його переміщення – вектор  Звичайно, не можна вважати, що швидкість тіла під час цього руху напрямлено вздовж вектора переміщення. Проведемо між точками А та В хорди  і вважатимемо, що на кожній з них тіло рухається прямолінійно, а вектор швидкості напрямлений уздовж хорди. Скорочуватимемо ці прямолінійні ділянки ∆ S. Ця ламана лінія стане більш схожа на плавну криву. Швидкість у кожній точці цієї кривої буде напрямлена по дотичній до кривої в цій точці

Вільне падіння тіл — це окремий випадок прямолінійного рівноприскореного руху без початкової швидкості. Вільне падіння — це рух тіл у вакуумі під дією однієї сили — сили тяжіння  . Прискорення при цьому однакове для всіх тіл. Цей факт підтверджується експериментально. Помістимо в трубку три різні предмети (свинцеву шротинку, корок і пташину пір’їнку). Потім швидко перевернемо трубку. Усі три тіла впадуть на її дно в такій послідовності: шротинка, корок і пір’їна (рис. 1). Так падають тіла тоді, коли в трубці є повітря. Якщо ж повітря з трубки відкачати насосом (рис. 2) і, закривши після відкачування кран, знову перевернути трубку (рис. 3), всі три тіла впадуть одночасно. Це й свідчить, що у вакуумі всі тіла падають з однаковим прискоренням.

Способи вимірювання прискорення земного тяжіння (вільного падіння):1. За допомогою математичного маятника шляхом вимірювання його довжини і періоду коливань. T.2. Вимірювання часу вільного падіння без початкової швидкості і використання формули: Основні формули для вільного падіння без початкової швидкості: Основні формули для тіла, яке у початковий момент мало вертикально напрямлену швидкість  0:

У XVII столітті панувала точка зору Аристотеля, який учив, що швидкість падіння тіла залежить від його маси. Чим важче тіло, тим швидше воно падає. Спостереження, які кожен з нас може виконати в повсякденному житті, здавалося б, підтверджують це. Спробуйте одночасно випустити з рук легку зубочистку і важкий камінь. Камінь швидше торкнеться землі. Подібні спостереження привели Аристотеля до висновку про фундаментальну властивість сили, з якою Земля притягує інші тіла. Насправді на швидкість падіння впливає не тільки сила тяжіння, але й сила опору повітря. Співвідношення цих сил для легких предметів і для важких різне, що і призводить до спостережуваного ефекту. Італієць Галілео Галілей засумнівався в правильності висновків Аристотеля і знайшов спосіб їх перевірити. Для цього він скидав з Пізанської башти в один і той же момент гарматне ядро і значно легшу кулю мушкета. Обидва тіла мали приблизно однакову обтічну форму, тому і для ядра, і для кулі сили опору повітря були настільки малі порівняно із силами тяжіння, що ними можна знехтувати. Галілей з’ясував, що обидва предмети досягають землі в один і той же момент, тобто швидкість їх падіння однакова. Результати, отримані Галілеєм,— наслідок дії закону всесвітнього тяжіння і закону, відповідно до якого прискорення, що набуває тіло, прямо пропорційне до сили, що діє на нього, і обернено пропорційне до маси.

Рівномірний рух матеріальної точки по колу

Рівномірний рух — механічний рух, під час якого тіло за певні проміжки часу проходить однаковий шлях. Одним із видів рівномірного руху є рівномірний прямолінійний рух, інший — рівномірне обертання, тобто обертання із сталою кутовою швидкістю. Швидкість рівномірного руху — фізична величина яка дорівнює відношенню переміщення до часу протягом якого це відбувається. Рівномірний рух — це рух, при якому тіло (точка) за будь-які рівні і нескінченно малі проміжки часу проходить однакову відстань. Вектор швидкості точки залишається незмінним, а її переміщення є добутком вектора швидкості на час:

Рівномірний прямолінійний рух – це рух, при якому тіло за будь-які рівні проміжки часу здійснює однакові переміщення. Наприклад, якщо ми розіб’ємо якийсь часовий інтервал на відрізки по одній секунді,то при рівномірному русі тіло буде переміщатися на однакову відстань за кожен з цих відрізків часу. Швидкість рівномірного прямолінійного руху не залежить від часу і в кожній точці траєкторії спрямована так, як і переміщення тіла. Тобто вектор переміщення збігається за напрямком з вектором швидкості. При цьому середня швидкість за будь-який проміжок часу дорівнює миттєвій швидкості: Швидкість рівномірного прямолінійного руху – це векторна фізична величина,дорівнює відношенню переміщення тіла   за будь-який проміжок часу до значення цього проміжку t:

Тіло, рухаючись, з часом переходить з однієї точки простору в іншу, описуючи певну траєкторію (лінію, вздовж якої воно рухається). Так от, довжина цієї траєкторії і буде визначати відстань, яку пройшло тіло за певний проміжок часу. Це теж фізична величина, яку називають шляхом. Вона характеризується лише числовим значенням і не має напряму. В системі  СІ шлях вимірюється в метрах. Коли тіло рухається, то за певний час воно проходить деякий шлях. Для різних тіл, що рухаються, цей шлях може бути різним. Наприклад, пішохід за годину пройде лише 5 км, а автомобіль за той самий час проїде 60 км. Порівнявши рух пішохода і автомобіля, можна сказати, що другий рухається швидше. Для порівняння руху різних тіл у фізиці використовують таку характеристику руху як швидкість.

Понад 5000 років тому жерці стародавнього Вавилону, спостерігаючи за Місяцем, визначили такий добре відомий нам інтервал часу, як тиждень. Як вони це зробили? У чому особливість руху Місяця? Чи зустрічається на Землі подібний рух? У цьому параграфі ви знайдете відповіді на ці та багато інших запитань.1. Знайомимося з рухом по колу. Спробуйте уявити лінію, вздовж якої рухаються малюк, що кружляє на каруселі, шкарпетка в барабані пральної машини в ході віджимання, кінчик ножа блендера під час виготовлення смузі чи коктейлю. Упевнені, що ви легко визначили: цією лінією є коло. Тож у зазначених випадках маємо справу з рухом по колу. Найпростішим є рівномірний рух по колу. Надалі, говорячи про рівномірний рух по колу будь-якого фізичного тіла, вважатимемо це тіло матеріальною точкою. Рівномірно по колу рухаються, наприклад, кабінки оглядового колеса. Близьким до рівномірного руху по колу є рух планет11 навколо Сонця (рис. 12.1, а), природного супутника (Місяця) або штучних супутників навколо Землі

Рівномірний рух матеріальної точки по колу — це такий криволінійний рух, у ході якого точка, рухаючись коловою траєкторією, за будь-які рівні інтервали часу проходить однаковий шлях.2 Визначаємо період обертання. Рівномірний рух по колу — це періодичний рух, тобто рух, який повторюється через певні рівні інтервали часу. Наприклад, кінчик секундної стрілки годинника, рухаючись рівномірно вздовж циферблата, повторює свій рух через кожні 60 с. Будь-який періодичний рух характеризується такими фізичними величинами, як період і частота. У разі рівномірного руху по колу говорять про період обертання та обертову частоту. Період обертання — це фізична величина, яка дорівнює часу, за який матеріальна точка, що рівномірно рухається по колу, здійснює один оберт. Період обертання позначають символом T. Одиниця періоду обертання в СІ — секунда:

Період обертання дорівнює 1 с, якщо за одну секунду здійснюється один оберт. Кінчик секундної стрілки годинника здійснює один оберт за 60 с, тому період його обертання, як і кожної точки секундної стрілки, дорівнює 60 с ( = 60 с). Поміркуйте, якими є періоди обертання точок хвилинної та годинної стрілок годинника. Коли збивають молочний коктейль блендером, кожна точка його ножа за 30 с робить 6000 обертів (рис. 12.3). Зрозуміло: щоб визначити час одного оберту, слід час обертання (t = 30 с) поділити на кількість обертів за30 сцей час N = 6000): T =-= 0,005 с = 5 мс . Тобто період обертання T то-6000чок ножа блендера становить 5 мс. Таким чином, щоб визначити період обертання Т, слід підрахувати кількість обертів М, здійснених за інтервал часу t, і скористатися формулою:

Як виміряти час? Відповідь на це запитання підказала людям сама природа. Річ у тім, що багато рухів, які відбуваються в природі, є періодичними, а період такого руху може слугувати одиницею часу. Наприклад, обертання Землі навколо своєї осі — періодичний рух. Щоденний схід (захід) Сонця, зумовлений цим рухом, підказав нашим прадавнім предкам природну одиницю часу — добу, яка дорівнює періоду обертання Землі навколо своєї осі. Кілька одиниць часу було винайдено в стародавньому Вавилоні. Спостерігаючи за нічним небом, жерці помітили, що «молодий» Місяць з’являється на небосхилі приблизно кожні 28 діб. Періодичне народження місячного диска слугувало своєрідним вічним «годинником». Так виникла одиниця часу місяць*. За цей час Місяць, обертаючись навколо Землі, проходить повний цикл зміни фаз: молодик, перша чверть, повня, остання чверть (рис. 12.5). Саме тому жерці розділили місячний місяць на чотири (за кількістю місячних фаз) й отримали сім днів — одиницю часу, яку називають тиждень.

Зараз у повсякденному житті ми використовуємо поняття календарного місяця, який не залежить від фаз Місяця і триває від 28 до 31 доби. Саме про цю швидкість ідеться, коли, наприклад, визначають швидкість руху людини, яка кружляє на каруселі, характеризують рух автомобіля на повороті, говорять про швидкість польоту штучних супутників Землі тощо. Підбиваємо підсумки. Рівномірний рух матеріальної точки по колу — це такий криволінійний рух, у ході якого точка, рухаючись коловою траєкторією, за будь-які рівні інтервали часу проходить однаковий шлях. Рівномірний рух по колу — це періодичний рух, тобто рух, який повторюється через певні однакові інтервали часу. Період обертання Т — це фізична величина, яка дорівнює часу, протягом якого тіло, що рівномірно рухається по колу, здійснює один оберт: Т = —, де t — час спостереження; N — кількість обертів за цей час. Оди-N

Спробуймо уявити або ж накреслити на папері траєкторію нашого руху до школи, на прогулянці до лісу чи в магазин і в кожному випадку зрозуміємо, що лінія, вздовж якої ми рухаємось, буде нагадувати криву. Такий рух надалі ми називатимемо криволінійним. Якщо детальніше розглянути траєкторію криволінійного руху, то можна помітити, що будь-яку, досить малу, ділянку траєкторії можна розглядати як частину руху по колу деякого радіуса. Звичайно, ми можемо створити умови, коли наша траєкторія нагадуватиме ламану лінію, але це штучно створений виняток, а не правило. Тому надалі розглянемо рух по колу як частину криволінійного руху. З курсу алгебри нам відомо, що довжина кола в 2π раз більша за його радіус або в π разів більша за його діаметр, тому маємо:

В багатьох практично важливих випадках для вивчення процесів генерації, поширення звукових хвиль та їх взаємодії з перешкодами використовується модель ідеальної стисливої рідини (газу) або ідеального пружного тіла. В цьому випадку процес поширення хвиль описується силовими характеристиками (тиск або тензор напружень) та кінематичними характеристиками (вектор коливальної швидкості частинок середовища. Коливальна швидкість виміряється в м/с або см/с. Зміна температури в процесі адіабатичної деформації частинок середовища може бути обчислена додатково. Для врахування втрат енергії при деформації середовища слід використовувати моделі, що враховують в'язкість. При поширенні гармонічних хвиль в'язкі втрати часто враховуються введенням комплексних хвильових чисел чи комплексних модулів пружності.