Епіграф уроку

„Той, хто серйозно прямує до пізнання істини, не повинен

займатися якоюсь однією наукою, бо всі вони взаємозв’язані”

/Рене Декарт/

Мета уроку:

1.Математична компетентність: закріпити навички, уміння учнів розв’язувати визначений інтеграл, домогтися засвоєння формули Ньютона -Лейбніца

2.Ключові компетентності:

спілкування державною мовою – доречно та коректно вживати в мовленні математичну термінологію; уміння вчитися впродовж життя – усвідомлювати цінність нових знань і вмінь

Фронтальне опитування

1. Що називається визначеним інтегралом?

Визначеним інтегралом від a до b неперервної функції  у = f(х), визначеної на проміжку [ a; b] , називається приріст первісної   F(x) для цієї функції

Фронтальне опитування

Яка існує формула для обчислення визначеного інтегралу?

Як називаються числа а, b?                                           f(x)  -?

Визначений інтеграл

Визначеним інтегралом від a до b неперервної функції  y = f (x) , визначеної на проміжку           , називається a;b приріст первісної           для цієї функції, тобтоF(x)

Формула

Ньютона-Лейбніца

Числа а і b називаються нижньою і верхньою межами інтегрування; f(x) – підінтегральна функція.

Портрети яких відомих вчених подано? Який вони внесли вклад в задачі на інтегрування?

І. Ньютон                       К. Лейбніц

            29.01.2022                                                                        http://aida.ucoz.ru                                             7

Фронтальне опитування

Який геометричний зміст інтегралу?

За допомогою визначеного інтегралу визначаємо  площу криволінійної трапеції

Який фізичний зміст інтегралу?

Знаходимо шлях (переміщення) матеріальної точки

29.01.2022                                                                                 http://aida.ucoz.ru                                             8

Основні правила і властивості визначеного інтеграла b b

1) f (x)dx = f (t)dt;

a                                                                                                                 a a

2) f (x)dx = 0;

a

b                                                                                                                 b

3)Cf (x)dx = C f (x)dx;

a                                                                                                                                                             a

b                                                                                                                                                             b     b

4)(f (x) g(x))dx = f (x)dx g(x)dx;

a                                                                                                                                                             a     a

b                                                                                                                                                             a

5) f (x)dx =− f (x)dx;

a                                                                                                 b

b                                                                                                 c  b

6) f (x)dx = f (x)dx + f (x)dx,ca;b;

                     a                            a                            c

bkx+ p = t,kb+p

7)^a f (kx+ p)dx = kdx =dtdt, = _k¹ ka^+pf (t)dt.

dx =

k

Обчисліть

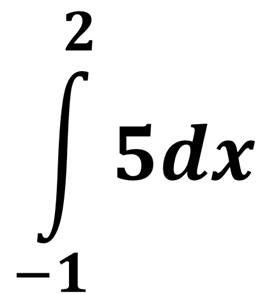
Відповідь

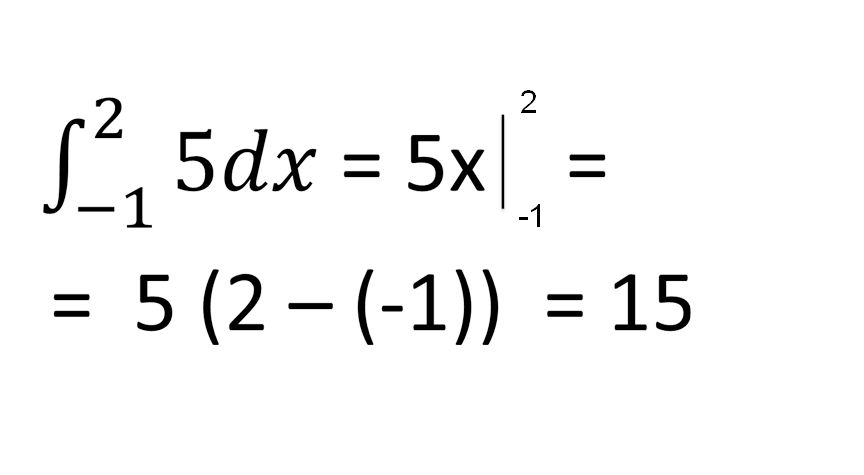
Обчислити

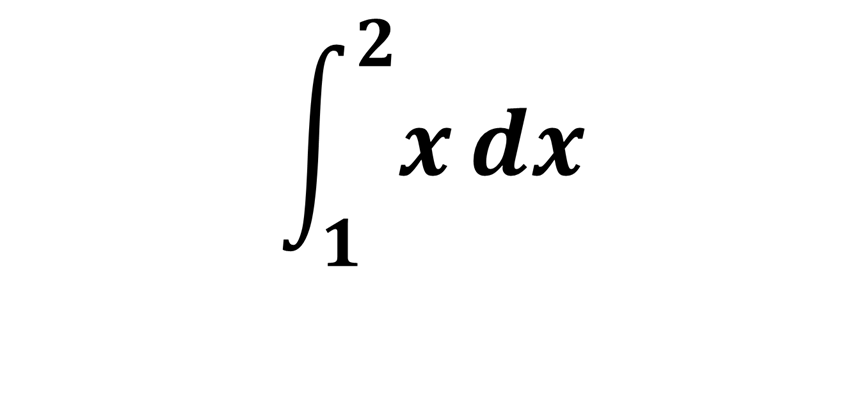
Відповідь

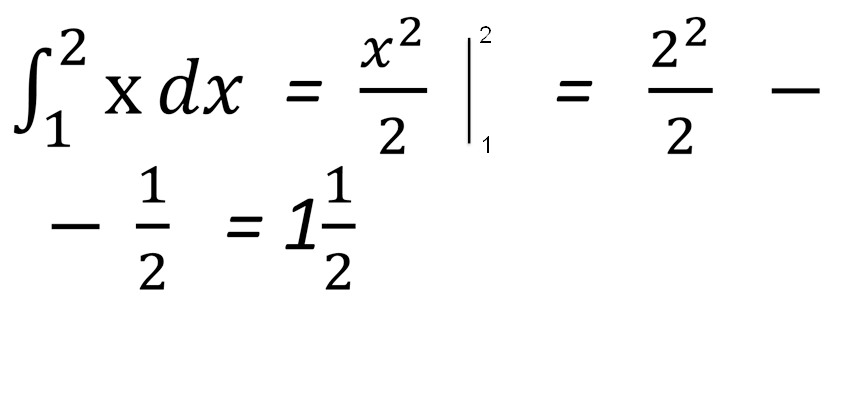
Обчислити

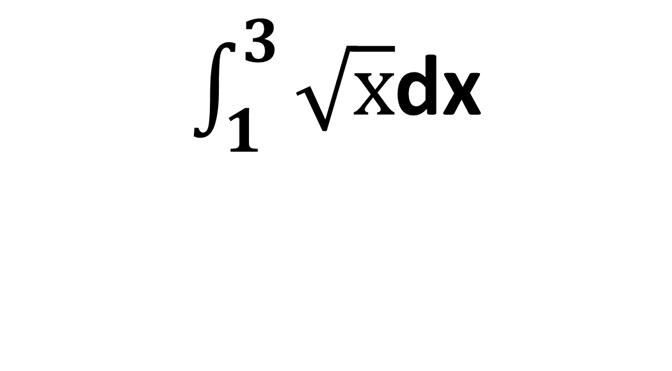
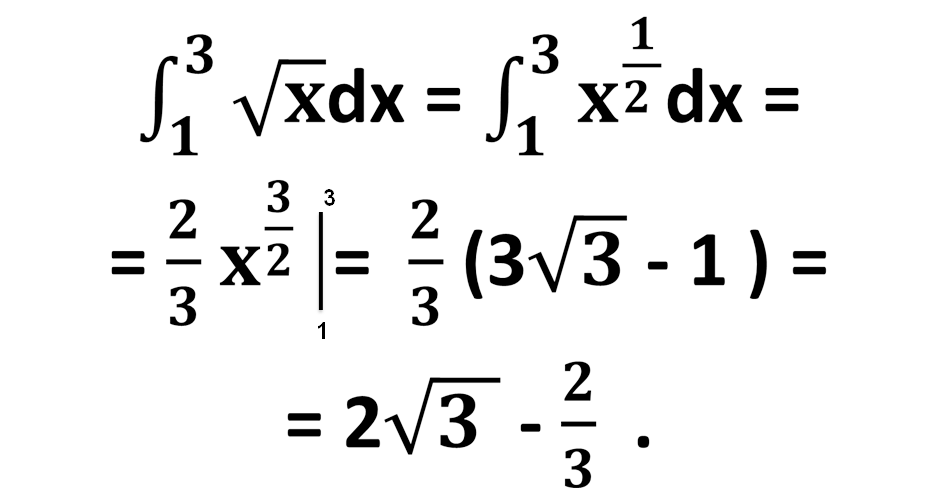
Відповідь

ОБЧИСЛИТИ

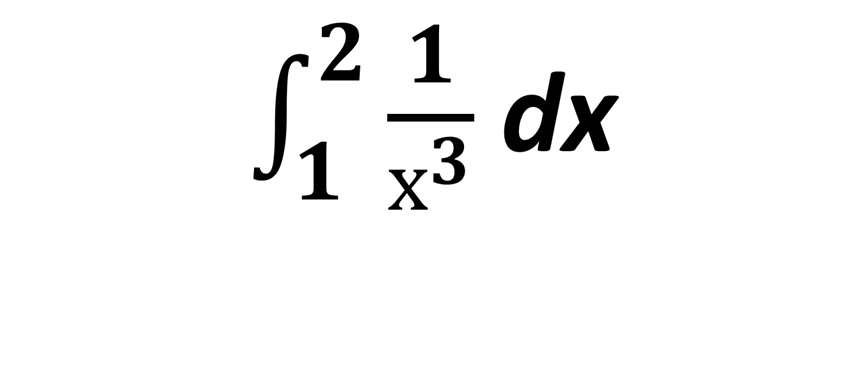
Відповідь

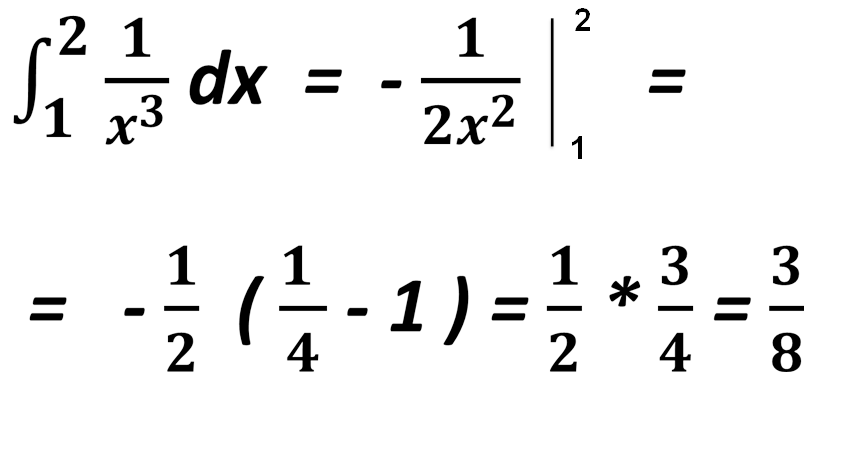
Обчисліть

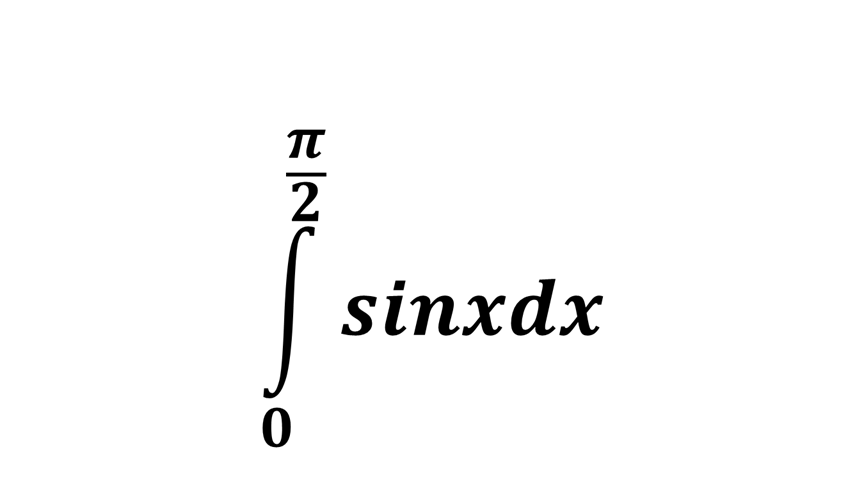
Відповідь

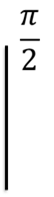= - cosx      =        

0

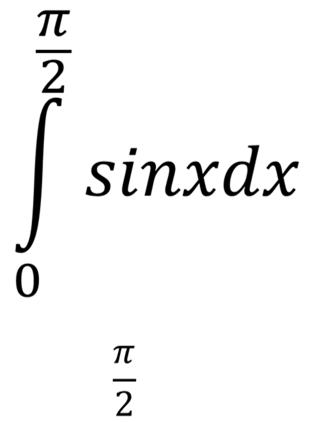=  - cos    + cos0 = 0 + 1 = 1

Обчислити

ВіДПОВІДЬ:

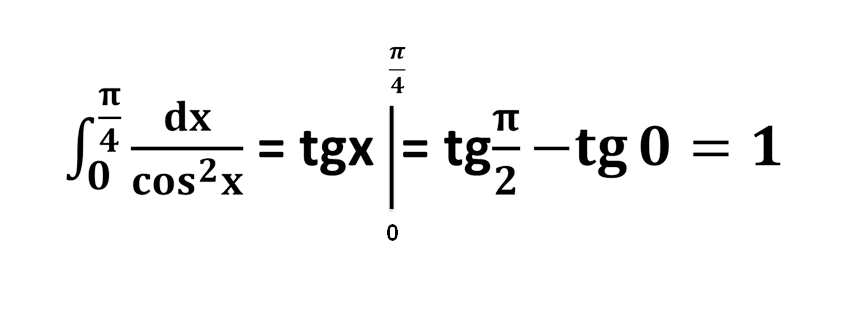
Обчислити

https://learningapps.org/view14763774

Самостійна робота

Підсумок уроку

1.           Над яким процесом працювали на уроці?

2.           Де застосовується даний процес?

3.           Що було найважче на уроці?

4.           Що сподобалося тобі на уроці?

Домашня робота

§2п11 (опрацювати)

№8,9 ст.67 – виконати письмово