Презентація " Формули скороченого множення в шкільній та позашкільній програмі"

Язовітченко Владислав учень 8 класу Краснопільської загальноосвітньої школи І-ІІІ ступенів Формули скороченого множенняв шкільній та позашкільнійпрограмі

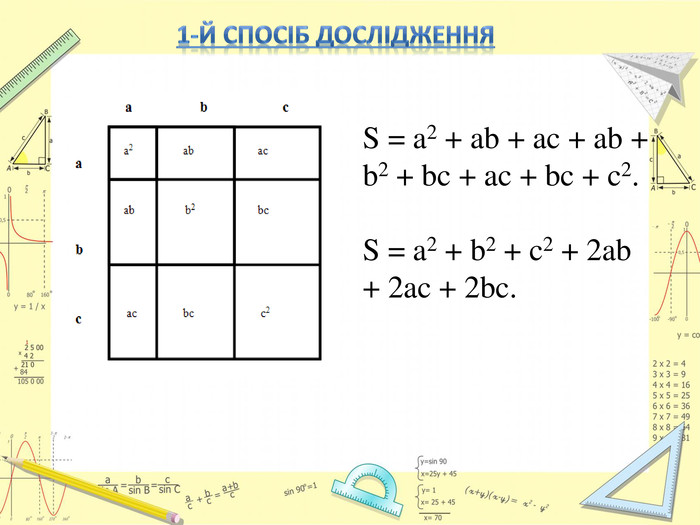
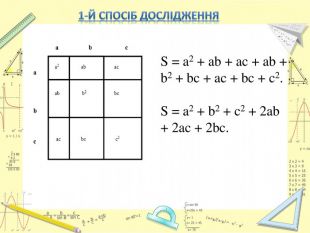
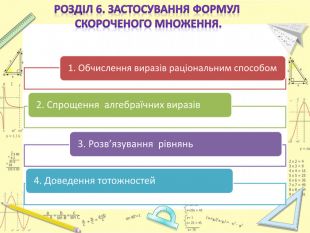
Актуальність дослідження: ця тема має велике значення в курсі математики і застосовується протягом усього періоду навчання. Мета дослідження : за допомогою доступних джерел і наукової літератури зібрати відомості з історії математики про формули скороченого множення, розглянути різні способи зведення в квадрат суми декількох доданків, вивчити способи піднесення в n - у степінь суми двох доданків. 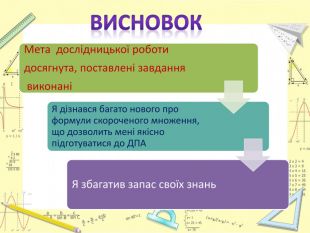Гіпотеза дослідження: в результаті дослідження я отримаю поглиблені знання з даної теми, а це буде сприяти розвитку логічного і творчого мислення в процесі вирішення проблемних завдань.

РОЗДІЛ 1. Історичні відомостіІсаак Ньютон. Рене Декарт. Блез Паскаль. Франсуа Вієт

1. Квадрат суми 2. Квадрат різниці 3. Різниця квадратів4. Куб суми 5. Куб різниці6. Сума кубів 7. Різниця кубів РОЗДІЛ 2. 7 формул шкільного курсу математики 7 магічнечисло

РОЗДІЛ 3. Зведення в квадрат суми кількох доданків(a + b + c)2 Способи дослідження:

1-й спосіб дослідження. S = a2 + ab + ac + ab + b2 + bc + ac + bc + c2. S = a2 + b2 + c2 + 2ab + 2ac + 2bc.

(а + b + c) ∙ (a + b + c) = a2 + ab + ac + ab + b2 + bc + ac + bc + c2 = a2 + b2 + c2 + 2ab + 2ac + 2bc.2-й спосіб дослідження3-й спосіб дослідження((а + b) + c) 2 = (a + b) 2 + 2 (a + b) c + c2 = a2 + c2 + b2 + 2ab + 2ac + 2bc.

У всіх трьох випадках результат отримав однаковий:(а + b + c) 2 = a2 + c2 + b2 + 2ab + 2ac + 2bc = a2 + c2 + b2 + 2 (ab + ac + bc) (а1 + a2 + ... + an) ² = a1² + a2² + ... + 2 (a1 a2 + a1 a3 + ... + aiaj + ... + an-1 a.), де i

Дослідив, як звести суму двох доданків в більш високу степінь: (a + b) 3 = (a + b) 2 (a + b) = a3 + 3a2b + 3ab2 + b3 (а + b) 4 = (a + b) 2 (a + b) 2 = (a2 + 2ab + b2) (a2 + 2ab + b2) = a4 + 4a3b + 6a2b2 + 4ab3 + b4 (а + b) 5 = (a + b) 2 (a + b) 3 = (a2 + 2ab + b2) (a3 + 3a2b + 3ab2 + b3) = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 РОЗДІЛ 4. Зведення многочлена в n - у степінь

Зведення многочлена в n - у степінь(а + b) 6 = (a + b) 2 (a + b) 4 = (a2 + 2ab + b2) (a4 + 4a3b + 6a2b2 + 4ab3 + b4) = a6 + 6a5b + 15a4b2 + 20a3b3 + 15a2b4 + 6ab5 + b6(a + b) 7 = (a + b) 3 (a + b) 4 = (a3 + 3a2b + 3ab2 + b3) (а4 + 4a3b + 6a2b2 + 4ab3 + b4) = a7 + 7a6b + 21a5b2 + 35a4b3 + 35a3b4 + 21a2b5 + 7ab6 + b7( a + b)n = an + a1an-1b + a2an-2b2 +…… + an-1abn-1 + bn , де 1, a1, …., an-1 коефіцієнти цього розкладу 

Трикутник Паскаля - нескінченна числова таблиця, виконана у формі трикутника, кожне число його дорівнює сумі двох чисел, які розташовані над ним. РОЗДІЛ 5. Трикутник Паскаля(a + b) 7 = a7 + 7a6b + 21a5b2 + 35a4b3 + 35a3b4 + 21a2b5 + 7ab6 + b7 (a - b) 7 = a7 - 7a6b + 21a5b2 - 35a4b3 + 35a3b4 - 21a2b5 + 7ab6 - b7

РОЗДІЛ 6. Застосування формул скороченого множення.

ВИСНОВОК