Презентація "Фрактали" (для роботи в МАН)







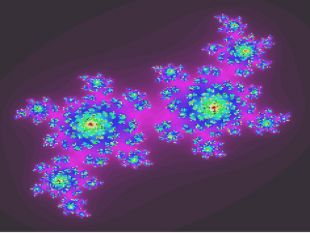
![МНОЖИНА МАНДЕЛЬБРОТА В якості прикладу розглянемо множину Мандельброта . Алгоритм його побудови досить простий і заснований на простому ітеративному вираженні: Z [i +1] = Z [i] * Z [i] + C МНОЖИНА МАНДЕЛЬБРОТА В якості прикладу розглянемо множину Мандельброта . Алгоритм його побудови досить простий і заснований на простому ітеративному вираженні: Z [i +1] = Z [i] * Z [i] + C](/uploads/files/925610/218174/234114_images/10.jpg)



























Мета даної роботи: З'ясувати, що таке фрактал; виділити основні види фракталів.з'ясувати, в яких областях науки і техніки використовуються фрактали. Завдання дослідження: Опрацювати і проаналізувати літературу по темі дослідження.розглянути різні види фракталів, їх класифікацію.зібрати колекцію фрактальних образів для первинного ознайомлення зі світом фракталів.ppt_xxshearppt_xppt_xxshearppt_xppt_xxshearppt_xppt_xxshearppt_x
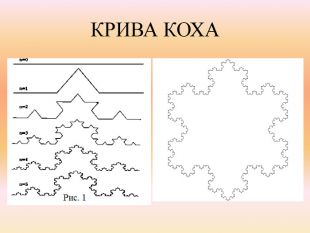
L-СИСТЕМИНайбільш простий спосіб побудови фракталів — це метод побудови за допомогою L - систем. Даний метод був розроблений Арістрідом Лінденмайером. Даний спосіб побудови фракталів здійснюється за допомогою простої, але достить ефективної технології комп`ютерної графіки — “черепашечна графіка”. В основі даного виду комп`ютерної графіки лежить черепашка, яка «повзає» по площині, малюючи за собою лінію.
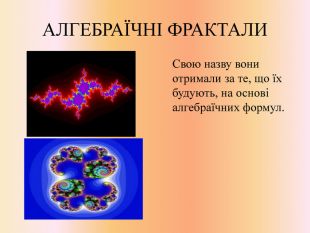
МЕТОД СИСТЕМ ІТЕРІРУЄМИХ ФУНКЦІЙДаний метод був розроблений і втілений в життя американським математиком М. Барнслі . Це метод складніший і гнучкіший, ніж метод L - систем . На відміну від методу L - систем він описує фрактали не графічно, а мовою математики. IFS дозволяє будувати більш складні фрактали, ніж метод L - систем . У ньому можна будувати такі знамениті фрактали як: множина Жюліа, фрактал Мандельброта та інші. У IFS для роботи з фракталами використовують комплексні числа і комплексну площину. Даний метод дозволяє побудувати безліч фракталів різних типів.
СЕРВЕТКА СЕРПІНСЬКОГО Для наочності візьмемо даний фрактал після одного перетворення. Він міститиме в собі чотири трикутника, один основний і три похідних від нього, мають номери t1, t2, t3 Розташуємо даний фрактал на комплексній площині, і для представлення координат будемо використовувати комплексні числа.
СЕРВЕТКА СЕРПІНСЬКОГОЗагальне рівняння серветки Серпінського для n-кутника можна записати у вигляді: Де i номер вершини многокутника, z i комплексна координата вершини основного многокутника, f i (z) перетворена комплексна координата. m це число більше 1, і яке входить в вираз l / m , де l – це відстань між z і z i , яке показує відстань від вершини основного трикутника fi(z).
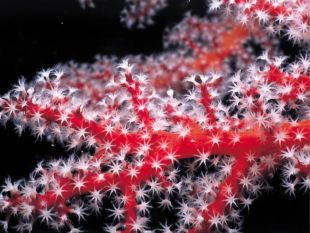
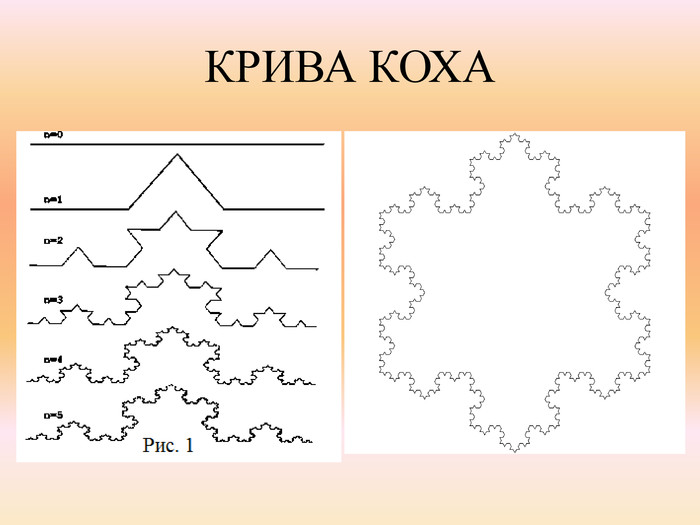
ВИСНОВКИТеорія фракталів має зовсім невеликий вік. Фрактал - це математична величина, що зустрічається досить часто. Фрактал - самоподібна фігура, зображення якої не залежить від масштабу.Існує 2 способи побудови фракталів Фрактали оточують нас повсюди: в природі, в комп'ютерних технологіях, їх використовують різні науки.


про публікацію авторської розробки
Додати розробку