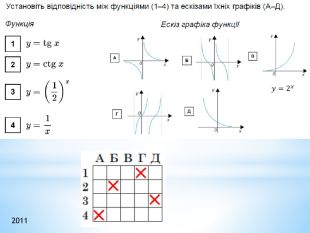
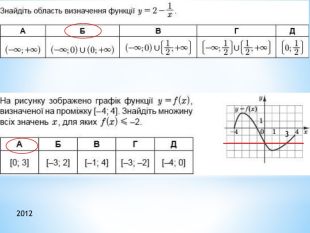
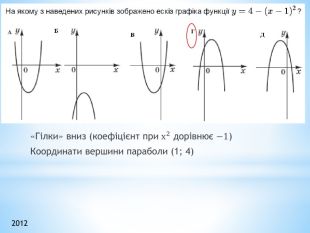
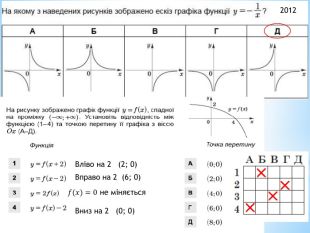
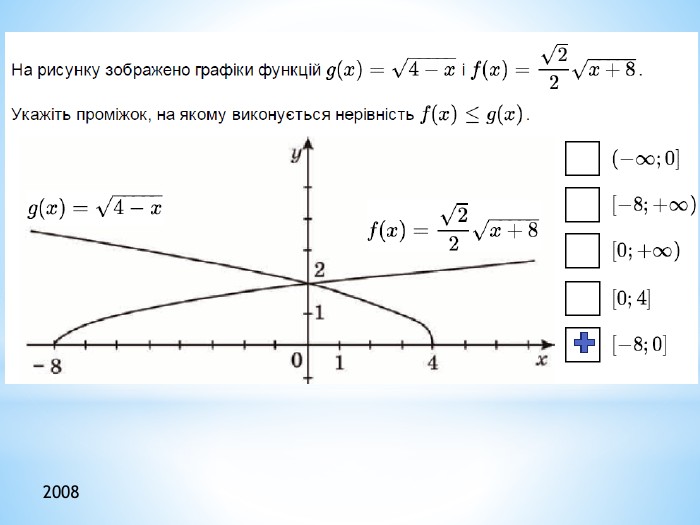
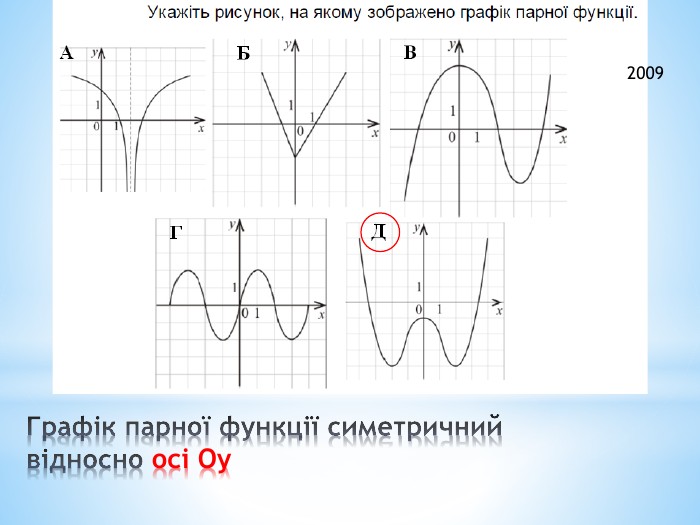
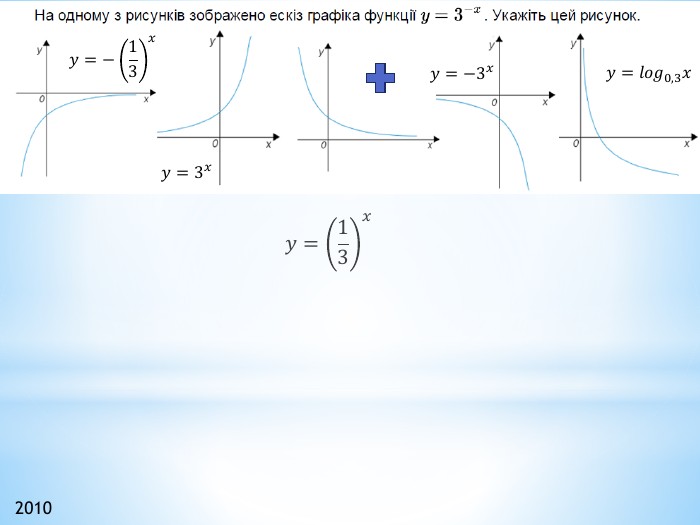
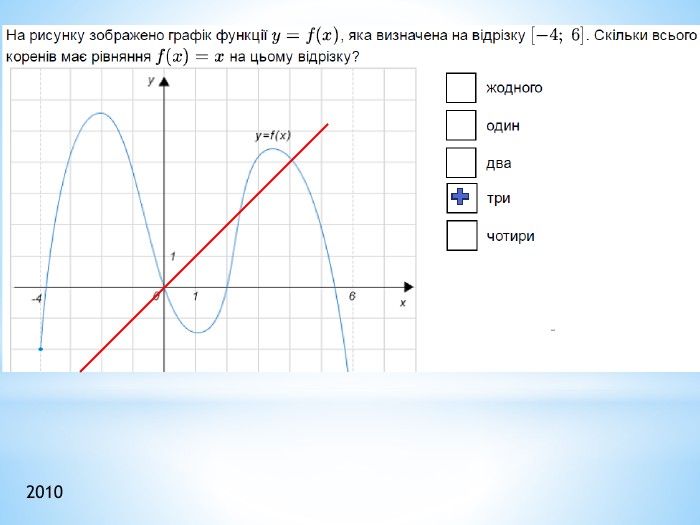
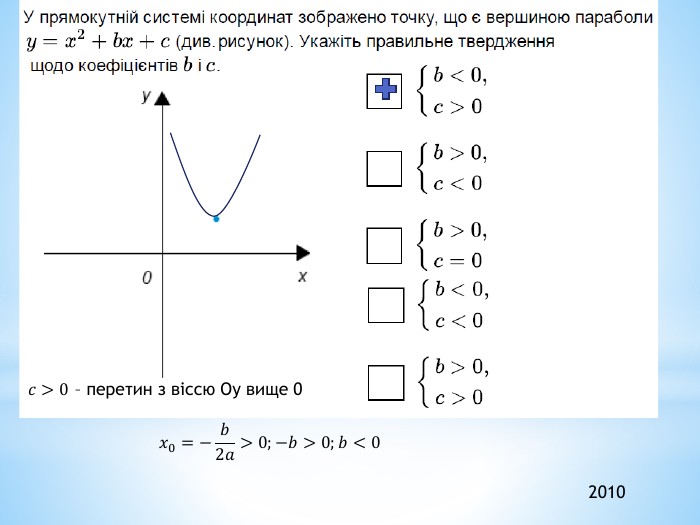
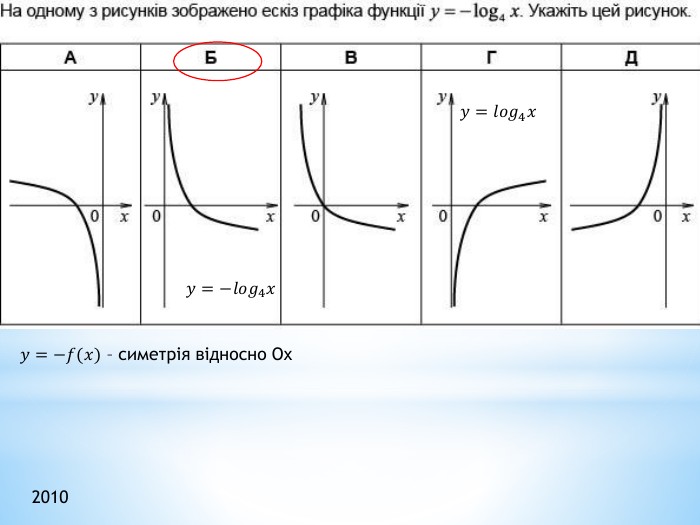
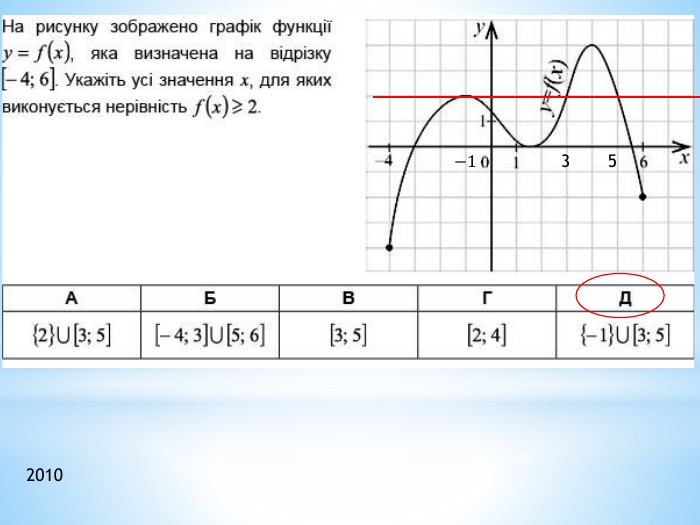
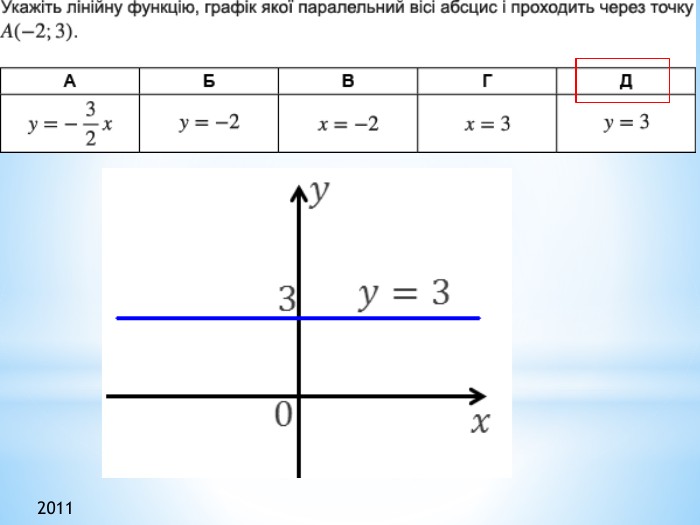
Презентація "Функції"










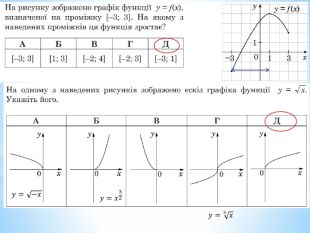
![2011 (34). На рисунку зображено графік функції 𝑦=𝑓(𝑥) , що визначена на проміжку (−∞;∞) і має лише три нулі. Розв’яжіть систему: 𝑓(𝑥)≥0𝑥2+𝑥−6>0 . У відповідь запишіть суму всіх цілих розв’язків системи. 𝑥∈−1;6∪9 - розв’язок першої нерівностіДля другої: 𝑥1=−3; 𝑥2=2 – корені відповідного квадратного рівняння𝑥+3𝑥−2>0𝑥∈(−∞;−3)∪(2;∞) 𝑥∈(2;6]∪9 - загальний розв’язок системи Сума цілих: 3+4+5+6+9= 27 2011 (34). На рисунку зображено графік функції 𝑦=𝑓(𝑥) , що визначена на проміжку (−∞;∞) і має лише три нулі. Розв’яжіть систему: 𝑓(𝑥)≥0𝑥2+𝑥−6>0 . У відповідь запишіть суму всіх цілих розв’язків системи. 𝑥∈−1;6∪9 - розв’язок першої нерівностіДля другої: 𝑥1=−3; 𝑥2=2 – корені відповідного квадратного рівняння𝑥+3𝑥−2>0𝑥∈(−∞;−3)∪(2;∞) 𝑥∈(2;6]∪9 - загальний розв’язок системи Сума цілих: 3+4+5+6+9= 27](/uploads/files/334031/299734/326998_images/22.jpg)
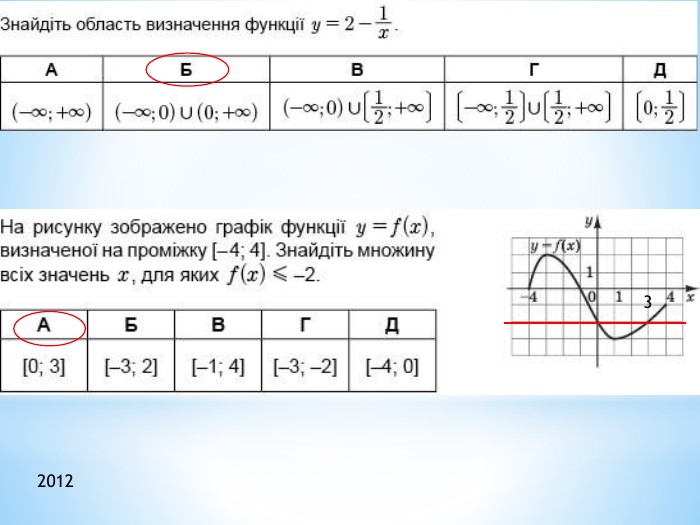
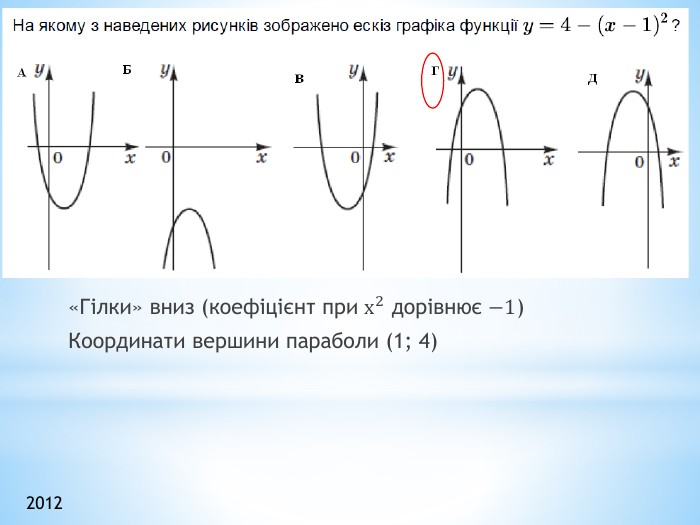



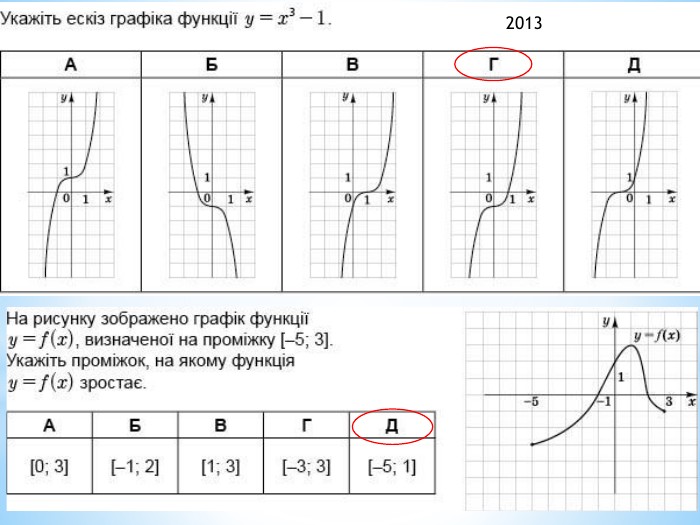

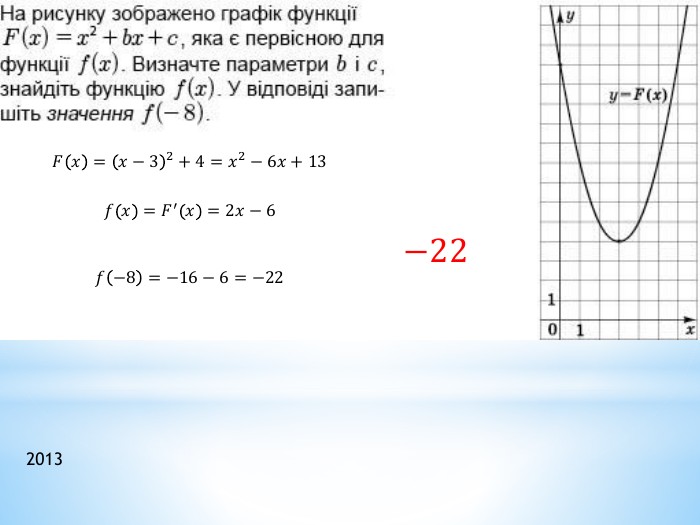
![𝑓𝑡=𝑡4 - зростає при 𝑡∈[0;∞)max1−2𝑐𝑜𝑠𝑥=3 при 𝑐𝑜𝑠𝑥=−1𝑚𝑎𝑥𝑦=342=812=40,5𝑓𝑡=𝑡4 - спадає при 𝑡∈(−∞;0]min1−2𝑐𝑜𝑠𝑥=−1 при 𝑐𝑜𝑠𝑥=1𝑚𝑎𝑥𝑦=142=12<40,5 2013 𝑓𝑡=𝑡4 - зростає при 𝑡∈[0;∞)max1−2𝑐𝑜𝑠𝑥=3 при 𝑐𝑜𝑠𝑥=−1𝑚𝑎𝑥𝑦=342=812=40,5𝑓𝑡=𝑡4 - спадає при 𝑡∈(−∞;0]min1−2𝑐𝑜𝑠𝑥=−1 при 𝑐𝑜𝑠𝑥=1𝑚𝑎𝑥𝑦=142=12<40,5 2013](/uploads/files/334031/299734/326998_images/33.jpg)



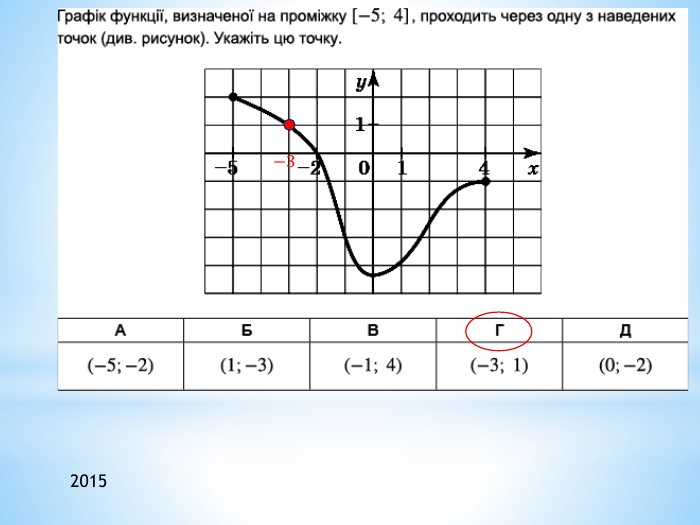




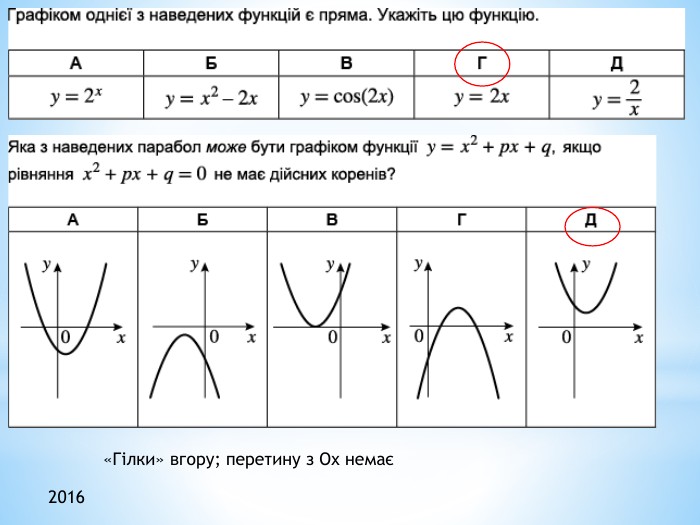
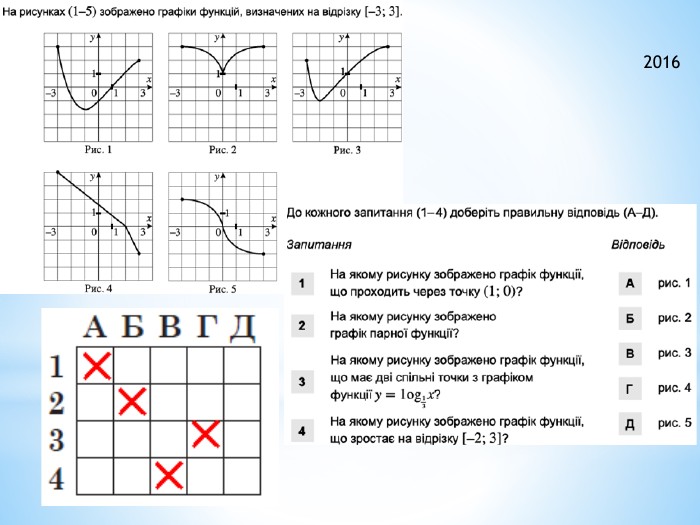

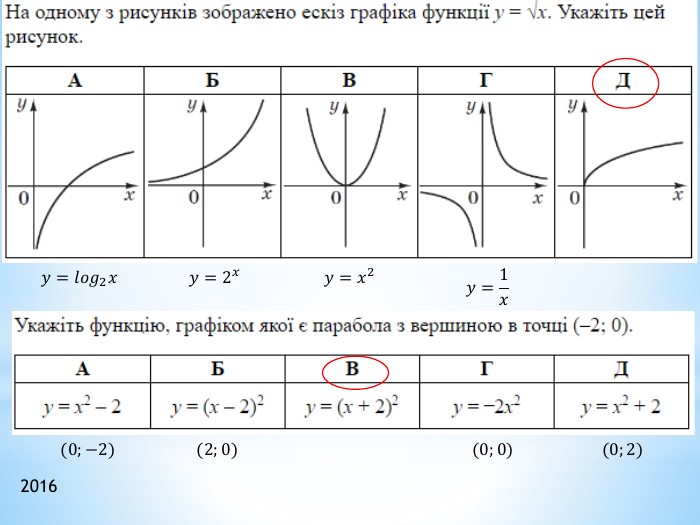

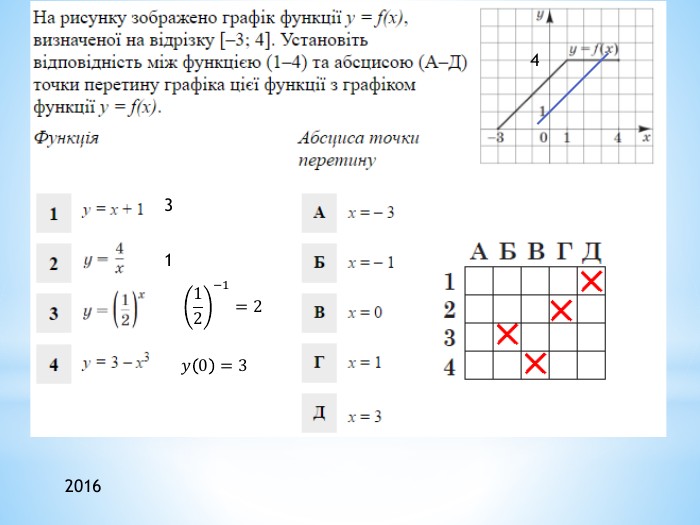
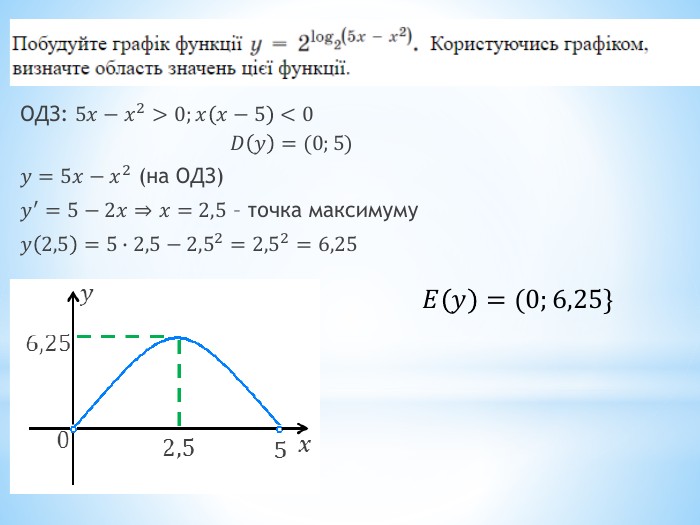
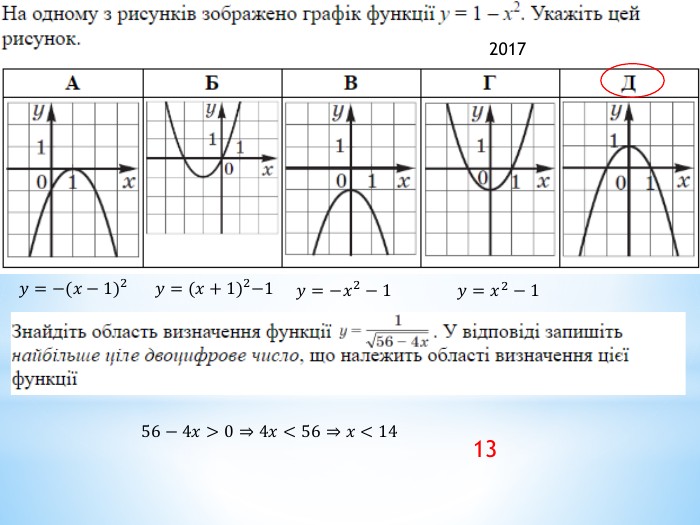
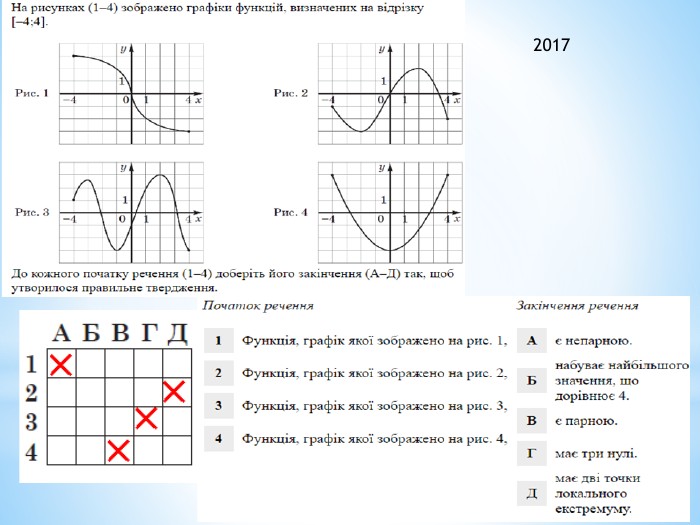
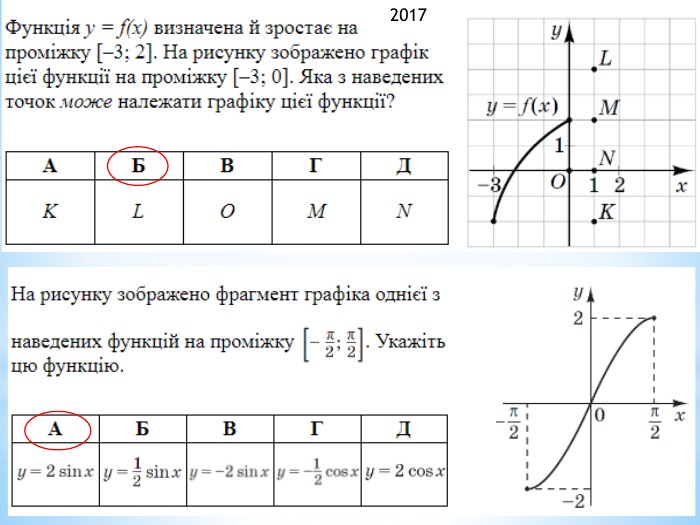
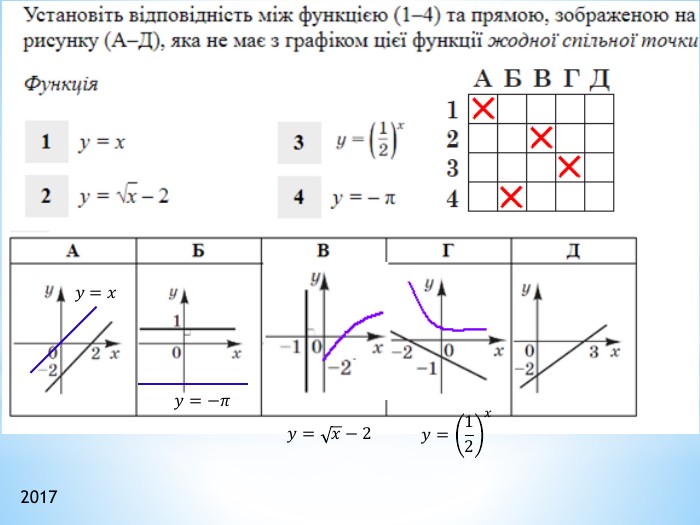

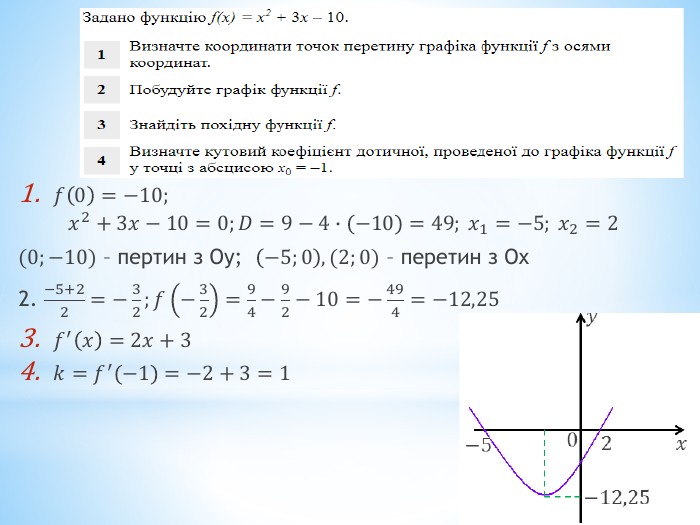


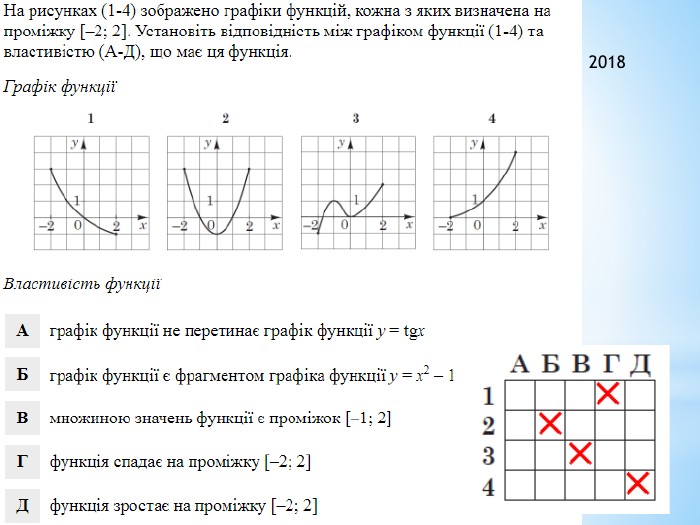
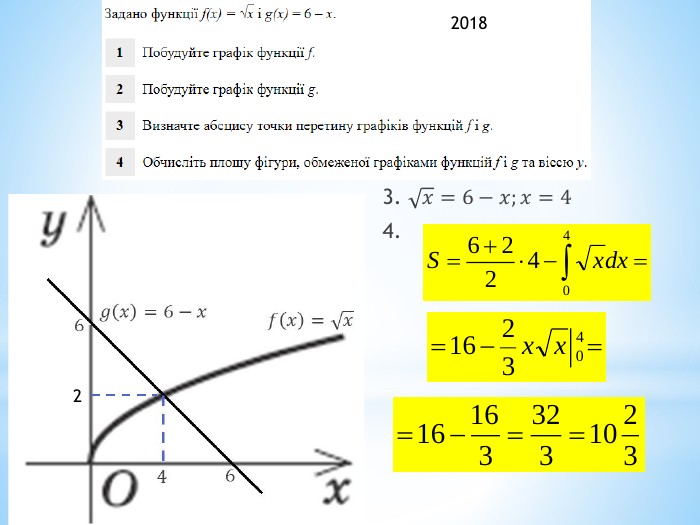
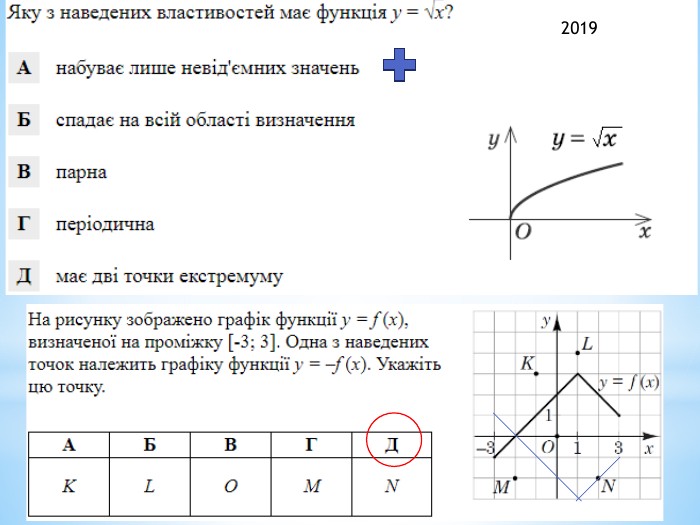
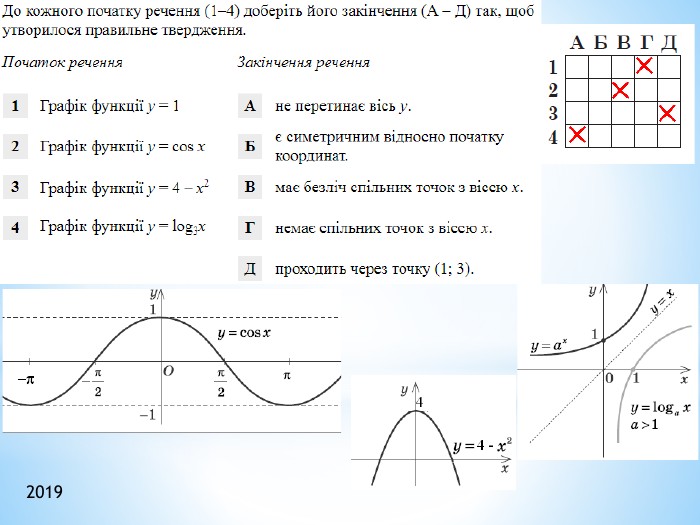
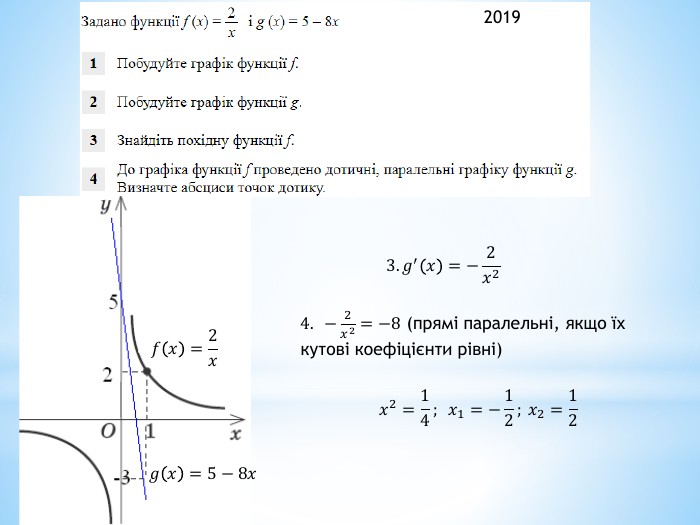
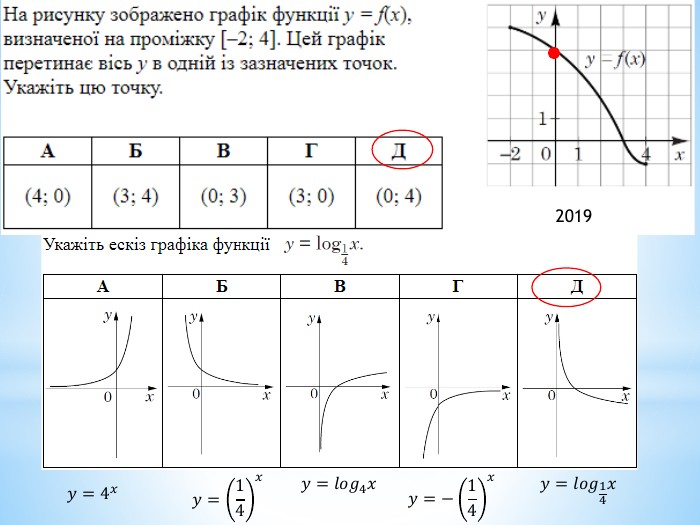


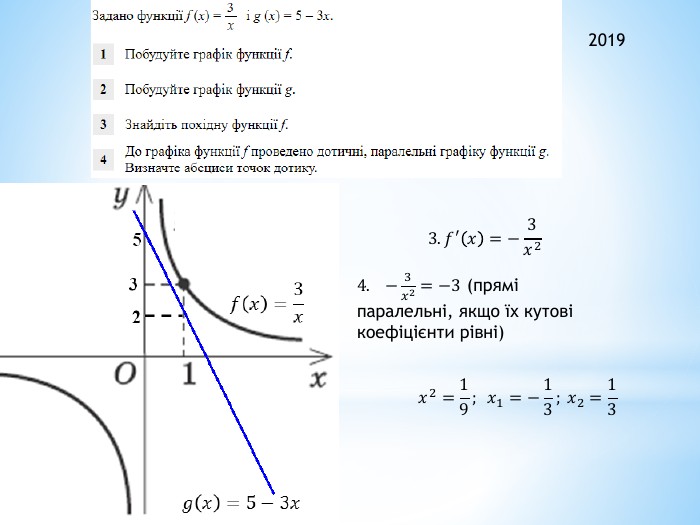
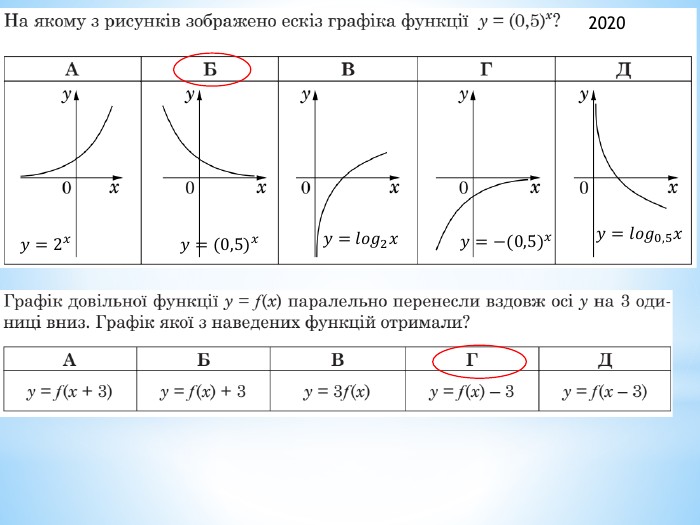




2011 (34). На рисунку зображено графік функції 𝑦=𝑓(𝑥) , що визначена на проміжку (−∞;∞) і має лише три нулі. Розв’яжіть систему: 𝑓(𝑥)≥0𝑥2+𝑥−6>0 . У відповідь запишіть суму всіх цілих розв’язків системи. 𝑥∈−1;6∪9 - розв’язок першої нерівностіДля другої: 𝑥1=−3; 𝑥2=2 – корені відповідного квадратного рівняння𝑥+3𝑥−2>0𝑥∈(−∞;−3)∪(2;∞) 𝑥∈(2;6]∪9 - загальний розв’язок системи Сума цілих: 3+4+5+6+9= 27
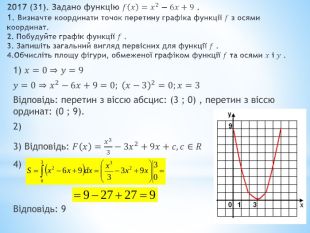
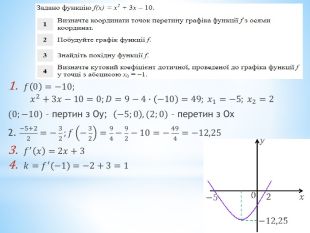
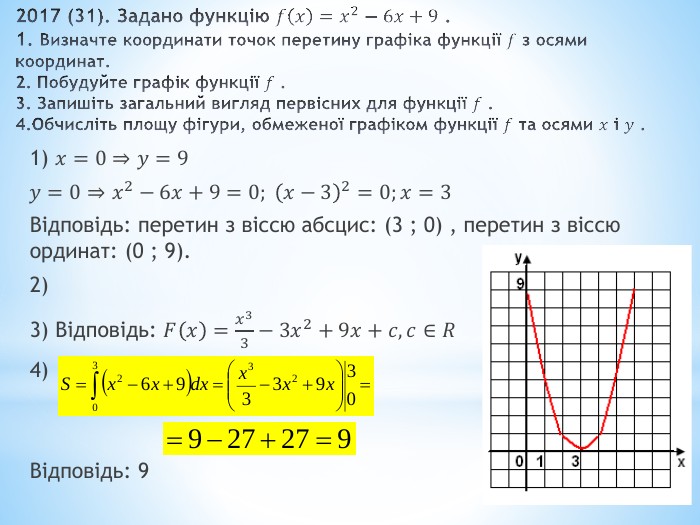
2017 (31). Задано функцію 𝑓𝑥=𝑥2−6𝑥+9 .1. Визначте координати точок перетину графіка функції 𝑓 з осями координат.2. Побудуйте графік функції 𝑓 .3. Запишіть загальний вигляд первісних для функції 𝑓 .4. Обчисліть площу фігури, обмеженої графіком функції 𝑓 та осями 𝑥 і 𝑦 . 1) 𝑥=0⇒𝑦=9𝑦=0⇒𝑥2−6𝑥+9=0; 𝑥−32=0;𝑥=3 Відповідь: перетин з віссю абсцис: (3 ; 0) , перетин з віссю ординат: (0 ; 9).2) 3) Відповідь: 𝐹𝑥=𝑥33−3𝑥2+9𝑥+𝑐, 𝑐∈𝑅4) Відповідь: 9
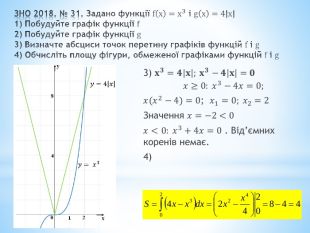
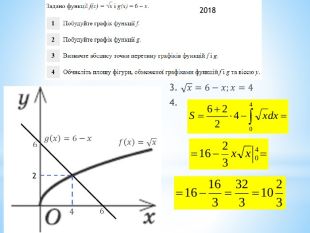
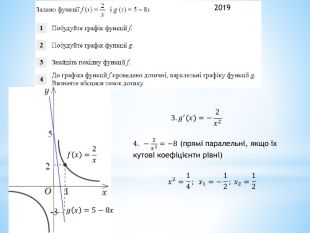
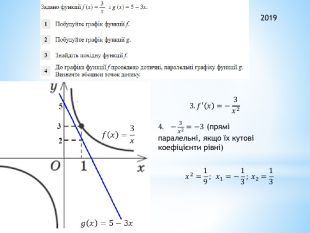
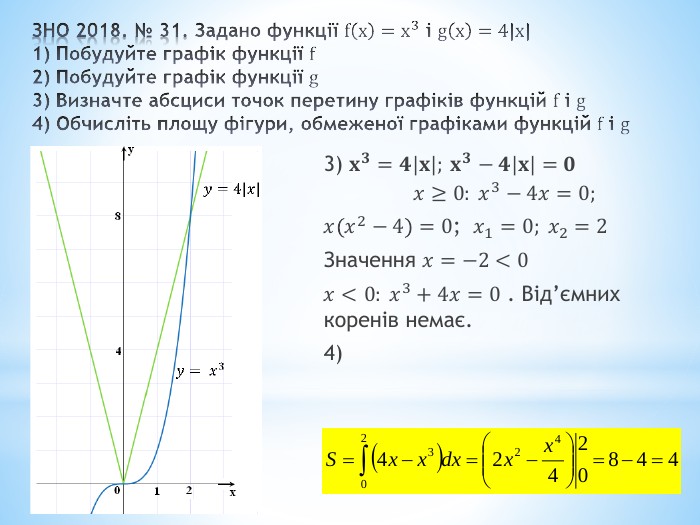
ЗНО 2018. № 31. Задано функції fx=x3 і gx=4|x|1) Побудуйте графік функції f2) Побудуйте графік функції g3) Визначте абсциси точок перетину графіків функцій f і g4) Обчисліть площу фігури, обмеженої графіками функцій f і g 3) 𝐱𝟑=𝟒𝐱; 𝐱𝟑−𝟒𝐱=𝟎𝑥≥0: 𝑥3−4𝑥=0;𝑥𝑥2−4=0; 𝑥1=0; 𝑥2=2 Значення 𝑥=−2<0𝑥<0: 𝑥3+4𝑥=0 . Від’ємних коренів немає.4)

про публікацію авторської розробки
Додати розробку