Презентація "Геометричні уявлення про число Пі"

«Геометричні уявлення про число π»

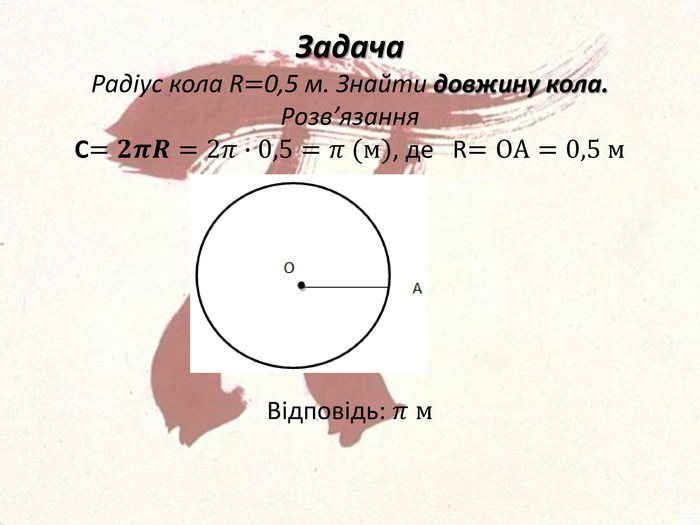
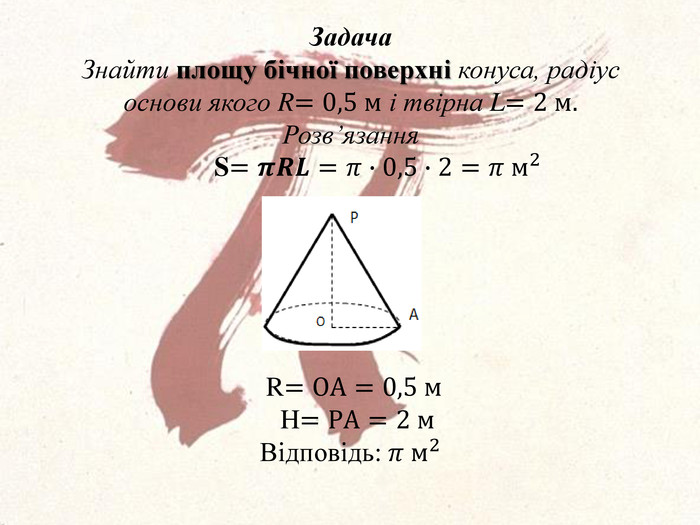
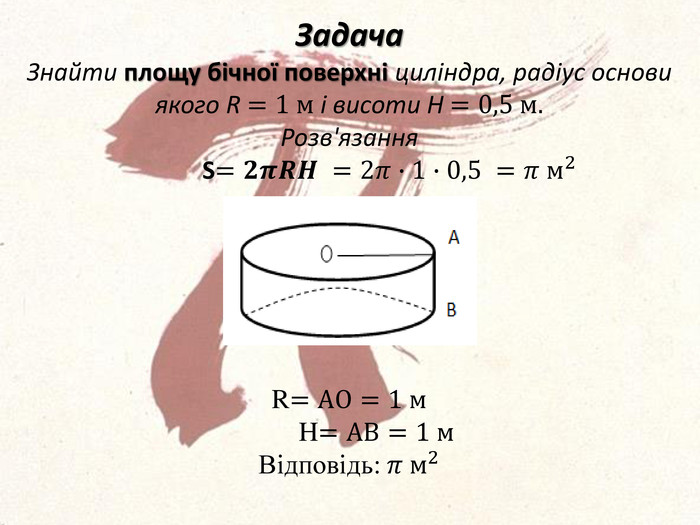
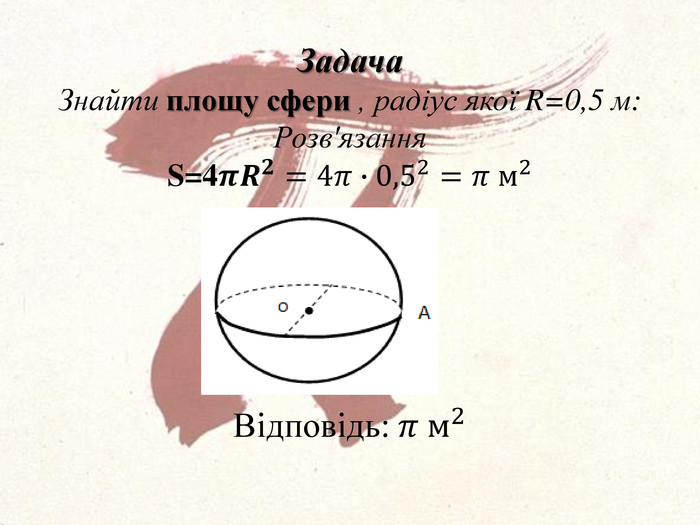
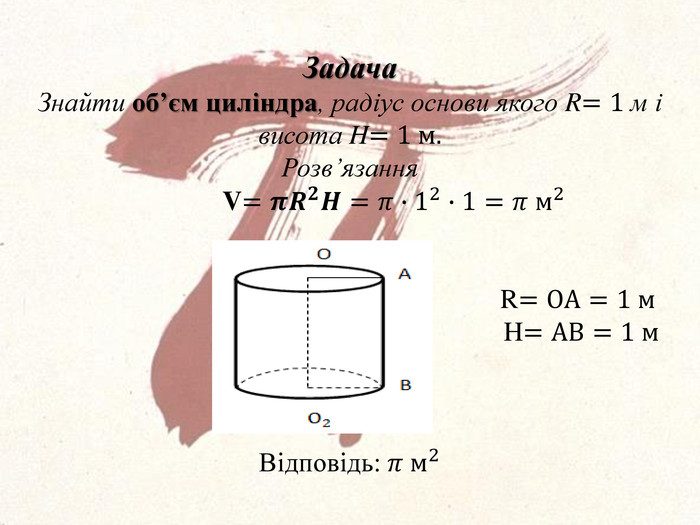
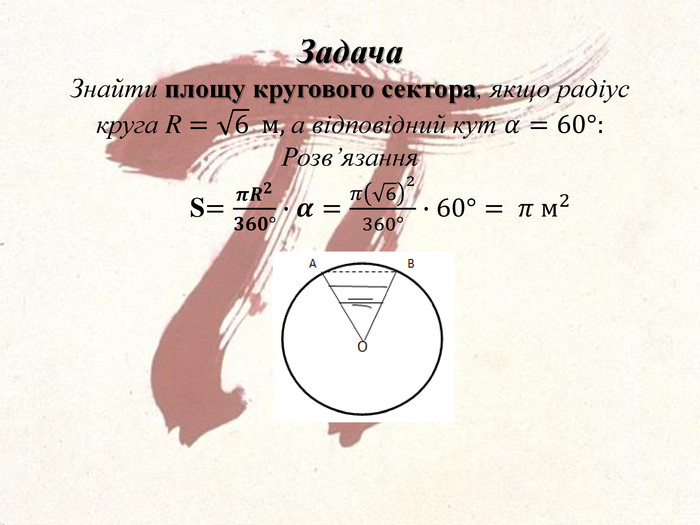
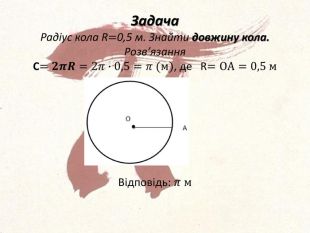
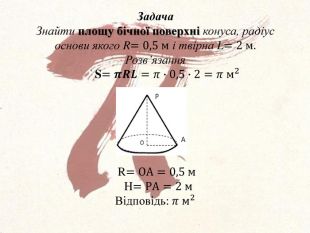
Об‘єкт, мета і методи дослідження Об‘єктом дослідження є число 𝜋 пі та історія його обчислення. Мета дослідження – знайти цікаві історичні факти про магічне число 𝜋 пі, що пов’язані з його появою та обчисленням . Розв’язуючи нескладні геометричні задачі з планіметріі та стереометрії представити число 𝜋 у вигляді міри якого – небудь геометричного об’єкта, тобто дати наочне уявлення про число 𝜋 . Методи дослідження – самостійно – пошуковий, аналітичний, метод теоретичного аналізу відповідної математичної літератури, систематизації 

Що це?Число π виникло в геометрії як відношення довжини кола до довжини його діаметра. Позначається буквою грецького алфавіту «пі».Інша назва – число Лудольфа.

Історія. Найперші відомі записані свідчення наближень числа  датуються близько 1900 року д.н. е.; це 256/81 ≈ 3.160 (Єгипет) і 25/8 = 3.125 (Вавилон), обидва в межах 1 відсотка від дійсного значення.

Розрахунки Архімеда. Архімед (287—212 до н.е) першим запропонувавметод обчислення математичним способом. Для цьоговін вписував у коло і описував біля нього правильнібагатокутники. Приймаючи діаметр кола за одиницю,Архімед розглядав периметр вписаного багатокутникаяк нижню оцінку довжини кола, а периметр описаногобагатокутника як верхню оцінку. Таким чином,для шестикутника виходить  3<π<2√3.

Перше тисячоліття. Близько 480 року китайський математик Цу Чунчжі продемонстрував. що π ≈ 355/113 (≈ 3.1415929), і показав що 3.1415926 <π< 3.1415927, Це значення залишалось найточнішим наближенням  протягом 900 років.

Друге тисячоліття. До другого тисячоліття н. е. число  було розраховане з точністю не більшою ніж 10 цифр в записі числа. Перший значний європейський внесок з часів Архімеда зробив німецький математик Лудольф ван Цейлен (1536—1610). Він витратив десять років на обчислення числа з 20-ма десятковими цифрами (цей результат був опублікований у 1596 році). Виклавши свої результати в творі «Про коло» («Van den Cirkel»), Лудольф закінчив його словами: «У кого є бажання, хай йде далі».

Наші дніУ 2002 році японський вчений прорахував 1,24 трильйона цифр в числі Пі за допомогою потужного комп'ютера Hitachi SR 8000. У жовтні 2011 року число π було розраховано з точністю до 10.000.000.000.000 знаків після коми.

Цікаві факти. Число Пі - найвідоміша константа в математичному світі. Символ Пі (π) використовується в математичних формулах вже протягом 250 років. Ми ніколи не зможемо з точністю виміряти окружність або площа кола, тому що не знаємо повне значення числа Пі. Дане «магічне число» є ірраціональним, тобто його цифри вічно змінюються у довільній послідовності.

Цікаві факти. Практично, фізикам потрібно тільки 39 цифр числа  , щоб зробити коло розміром як видимий всесвіт з точністю до розміру атома водню. Якщо розрахувати довжину екватора Землі з використанням числа π з точністю до дев'ятого знака, помилка в розрахунках складе близько 6 мм. У 1995 році Хірюкі Гото зміг відтворити по пам'яті 42195 знаків числа Пі після коми, і до цих пір вважається дійсним чемпіоном у цій галузі.

“Пі” чи “тау”?Вчені наполягають на необхідності зміни шкільних підручників на нові, які будуть використовувати тау, значення якої в два рази більше пі, і дорівнює приблизно 6,28. Оскільки в більшості формул використовується тау (або два пі), то саме воно повинно зайняти місце пі в якості константи кола.«Математики не вимірюють кути в градусах, ми вимірюємо їх в радіанах, а в колі міститься 2 Пі радіан».

Обчислення такої великої кількості знаків у 𝝅 велося головним образом із теоретичних інтересів; для самих важких розрахунків в теперішній час рідко використовують більше десяти – п’ятнадцяти знаків. Запам’ятати перші 12 знаків 𝝅 легко за допомогою двовірша: “Это я знаю и помню прекрасно, их многие знаки мне лишни, напрасно”. Записавши кожне слово двовірша цифрою, рівній числу літер в ньому, ми і отримаємо 𝝅=𝟑,𝟏𝟒𝟏𝟓𝟗𝟐𝟔𝟓𝟑𝟓𝟖… 

Задача. Радіус кола R=0,5 м. Знайти довжину кола. Розв’язання. C=𝟐𝝅𝑹=2𝜋∙0,5=𝜋 (м), де R=ОА=0,5 м Відповідь: 𝜋 м  

Задача. Знайти довжину дуги кола радіуса R=3 м, яка відповідає центральному куту величиною n=60°. Розв’язання 𝒍=𝝅𝑹𝟏𝟖𝟎°∙n=𝜋∙3180°∙60°=𝜋 (м)R=ОА=ОВ=3 м. Відповідь: 𝜋 (м) 

Задача. Знайти площу круга, радіус якого R =1 м. Розв’язання S =𝝅𝑹𝟐=𝜋∙12=𝜋 м2 R = ОК =1 м. Відповідь: 𝜋 м2 

Задача Знайти площу бічної поверхні конуса, радіус основи якого R=0,5 м і твірна L=2 м. Розв’язання S=𝝅𝑹𝑳=𝜋∙0,5∙2=𝜋 м2 R=ОА=0,5 м H=РА=2 м. Відповідь: 𝜋 м2 

Задача. Знайти площу бічної поверхні циліндра, радіус основи якого R =1 м і висоти H =0,5 м. Розв'язання S=𝟐𝝅𝑹𝑯 =2𝜋∙1∙0,5 =𝜋 м2 R=АО=1 м H=АВ=1 м. Відповідь: 𝜋 м2 

Задача. Знайти площу сфери , радіус якої R=0,5 м: Розв'язання. S=4𝝅𝑹𝟐=4𝜋∙0,52=𝜋 м2 Відповідь: 𝜋 м2  

Задача. Знайти об’єм циліндра, радіус основи якого R=1 м і висота H=1 м. Розв’язання V=𝝅𝑹𝟐𝑯=𝜋∙12∙1=𝜋 м2  R=ОА=1 м H=АВ=1 м Відповідь: 𝜋 м2 

Задача. Знайти площу кругового сектора, якщо радіус круга R =6  м, а відповідний кут 𝛼=60°: Розв’язання S=𝝅𝑹𝟐𝟑𝟔𝟎°∙𝜶=𝜋62360°∙60°= 𝜋 м2 

Задача Знайти площу бічної поверхні зрізаного конуса, радіуси основ якого R=34 м, r=14 м і висота H=32 м. Розв’язання Твірна L=322+122=1 м,S=𝝅𝒓+𝑹𝑳=𝜋14+34∙1=𝜋 м2 

R=О1 В=34мr=О2 А=14 м. H=О1 О2=32 м L=АВ=1 см Для того щоб побудувати відрізок довжиною 32 м ( висота зрізаного конуса), можна побудувати відрізок довжиною 3, а потім поділити його на дві рівні частини за допомогою циркуля. Відповідь: 𝜋 м2  

В этот день весь мир ест ПИроги и ПИроженые, Играет на ПИанино и в ПИн-понг. Не пропустите - праздник начинается ровно в 1: 59 ночи!14 березня – міжнародний день числа

Пам’ятники числу π Пам’ятник числу π перед будівлею Музея мистецтв в місті Сіетл. Пам'ятник числу π, що знаходиться в Австралії в місті Сідней перед музеєм мистецтв. Всього таких пам’ятників в світі 10.

Трохи музики. Музикант David Macdonald записав як звучить число Pi з точністю до 122 знака після коми.