Презентація "Графічні методи розв’язування фізичних задач 1"

Графічні методи розв’язування фізичних задач. Частина 1

Продовжуючи розмову про застосування графіків функціональних залежностей в шкільному курсі фізики, як засіб візуалізації навчальної інформації розглянемо приклади задач з використанням графіків руху х = х (t).

Задача 1. На морській лінії Лондон – Нью–Йорк кожного дня опівдні за Гринвічем відпливають два теплоходи: один з Лондона до Нью–Йорка, другий – з Нью–Иорка до Лондона. Кожний теплохід рівно через тиждень опівдні за Гринвічем прибуває в порт свого призначення. Скільки геплоходів цієї лінії зустрічає кожний теплохід за час свого рейсу?

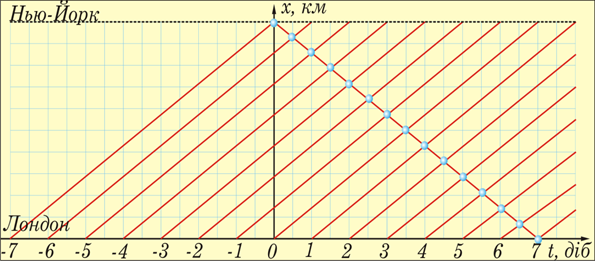
Рис. 1

Розв’язання. На рис. 1 зображено графік руху теплоходів, що відпливають від Лондона протягом двох тижнів, і графік руху одного з теплоходів, що прямує їм назустріч. З рисунка видно, що цей теплохід зустріне 13 теплоходів на лінії і ще 2 теплоходи в портах.

Задача 2. З Києва до Фастова з інтервалом 20 хв вирушили два електропотяги зі швидкостями 30 км/ год. Назустріч їм рухається пасажирський потяг, який зустрічає ці електропотяги з інтервалом 8 хв, визначити швидкість пасажирського потяга.

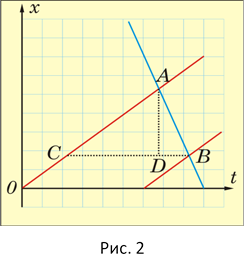
Розв’язання. Побудуємо графіки руху електропоїздів (1, 2) і пасажирського поїзда (З) (рис. 2). З рисунка видно, що BC = ОЕ = 20 хв.

Відрізок шляху AD пасажирський поїзд долає за 8 хв, а електропоїзди – за 12 хв (цей час визначається відрізком CD). Таким чином, ∙12 = u∙8, оскільки  = tg α а u = tg . Звідси u = 45 км/год.

Задача 3. Завод, де працює інженер, розташований за містом. Кожного разу до потяга, яким інженер прибуває на станцію, приїздить автомобіль і відвозить інженера на завод. Одного разу інженер прибув на станцію на годину раніше, ніж завжди, і, не чекаючи автомобіля, пішов до заводу. Через деякий час він зустрів автомобіль, який привіз інженера на 10 хв раніше, ніж в інші дні. Скільки часу інженер йшов пішки?

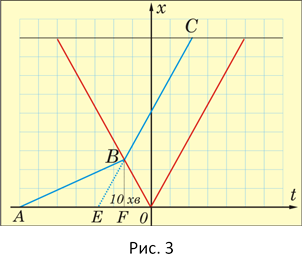Розв’язання. Графіки руху інженера і автомобіля (рис. 3) нахилені до вісі часу під різними кутами. Чому? Нехай точка О відповідає часу, коли інженер приїздить на станцію у звичайні дні. Суцільна тонка лінія – це графік руху автомобіля до станції та заводу у звичайні дні. Суцільна товста лінія – графік руху інженера: АВ – пішки; BC – автомобілем; ВЕ – додаткова побудова (продовження BC). Відрізок EO дорівнює 10 хв (ЕО = CD = 10 хв). Трикутник ВОЕ рівнобедрений, оскільки швидкість автомобіля стала за значенням. Тому FO = 5 хв, а AF = 55 хв. Отже, інженер ішов 55 хв.

Задача 4. Дорогою в одному напрямі зі сталими, але з різними швидкостями рухаються бігун, велосипедист і мотоцикліст. У момент часу, коли мотоцикліст наздогнав велосипедиста, бігун знаходиться попереду на відстані 15 км. Коли мотоцикліст наздоганяє бігуна, велосипедист відстає від них на 10 км. На якій відстані від бігуна знаходиться мотоцикліст у той момент часу коли його наздогнав велосипедист?

Розв’язання. Побудуємо графіки руху бігуна, велосипедиста і мотоцикліста (рис. 4). За початок відліку часу оберемо момент зустрічі велосипедиста й мотоцикліста. Нахил прямих, що є графіками руху, якісно відповідає їхнім швидкостям. Точки перетину графіків – місця зустрічі учасників руху. ОА= 15 км, BC = 10 км. Треба визначити DE. Правильну відповідь можна отримати швидко,

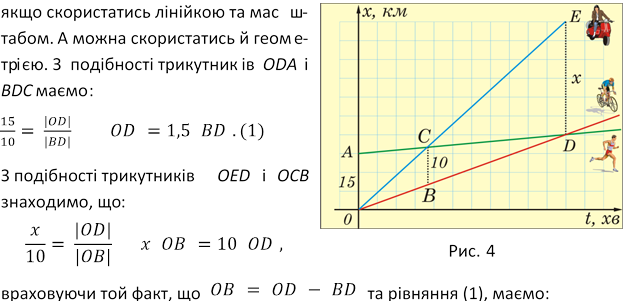
x (|OD| - |BD|) = 15 |BD|,

                                       x (1,5|BD| - |BD|) = 15 |BD|          

Отже, шукана відстань дорівнює 30 км.