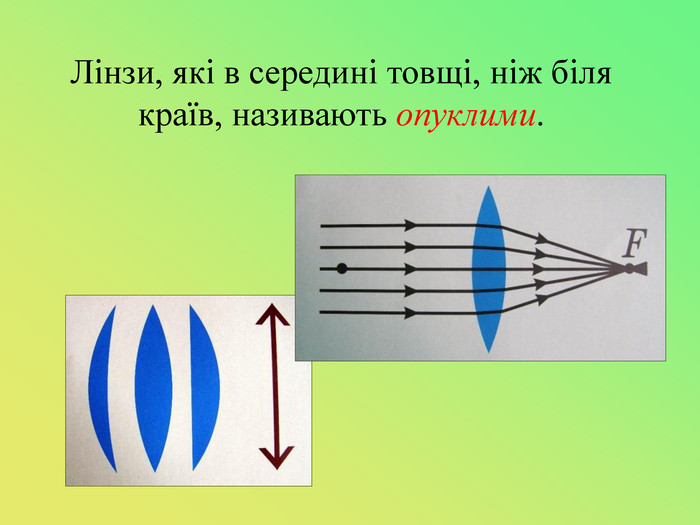
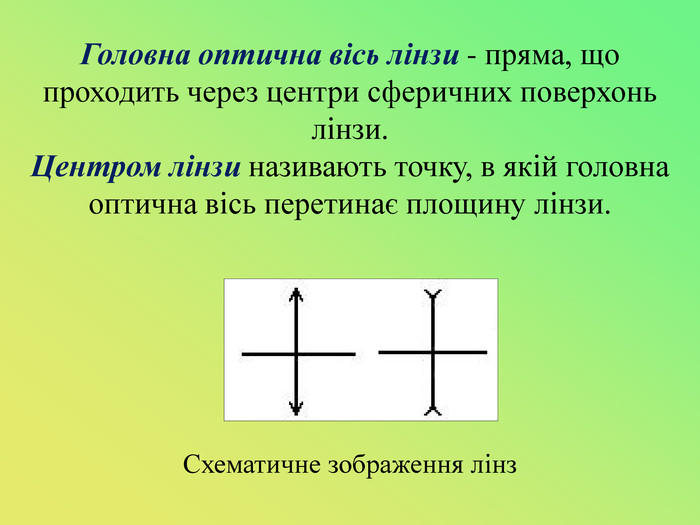
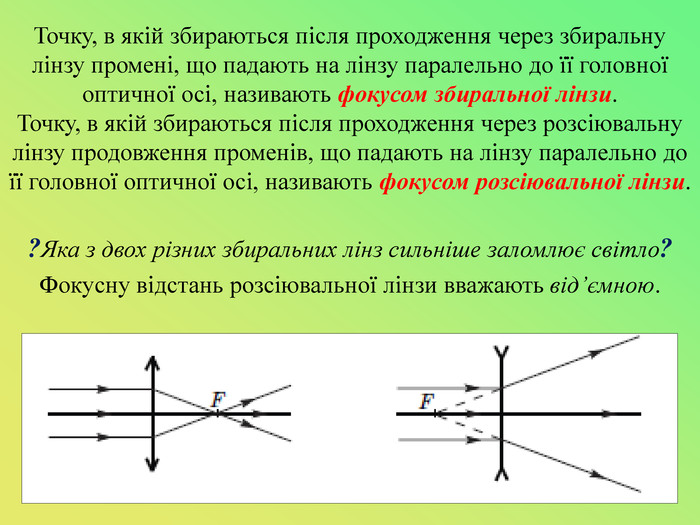
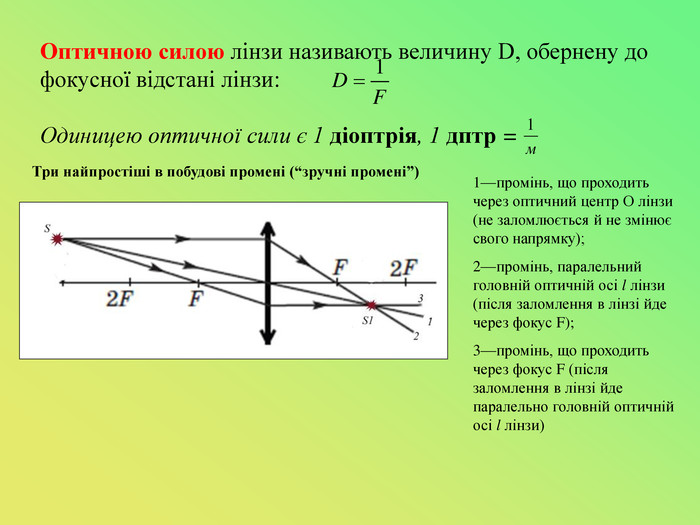
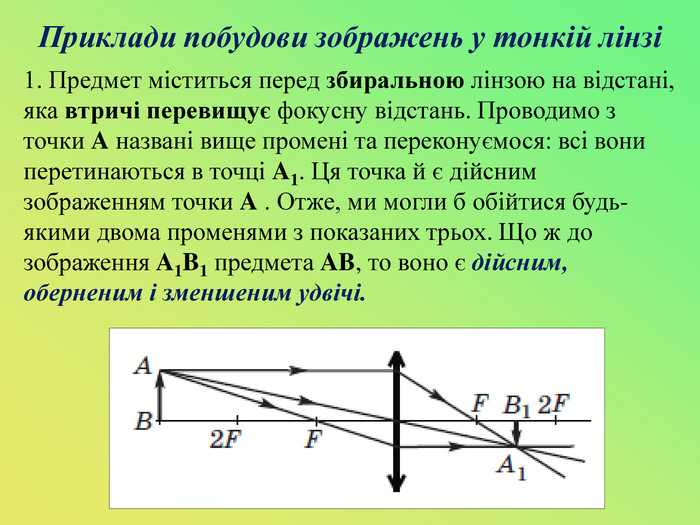
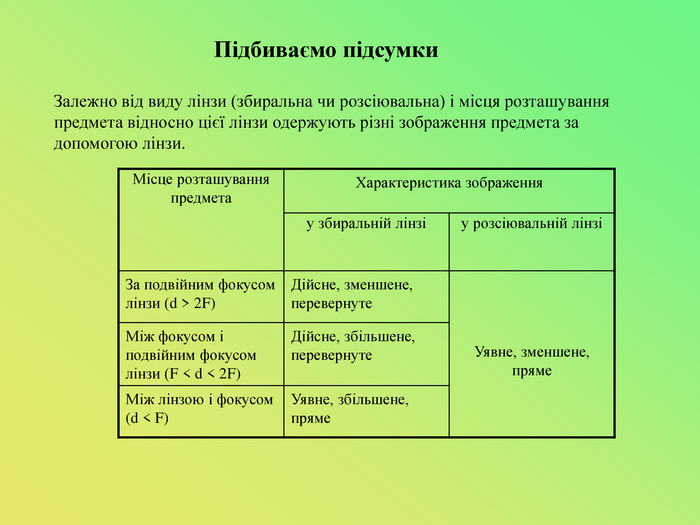
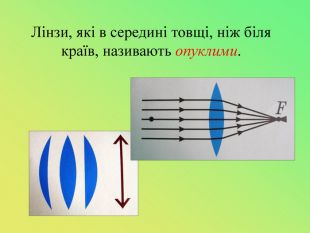
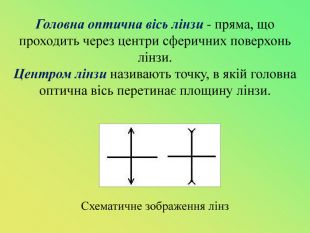
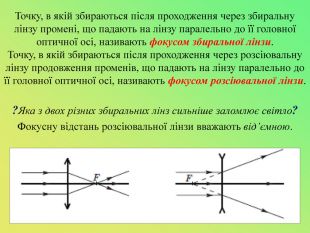
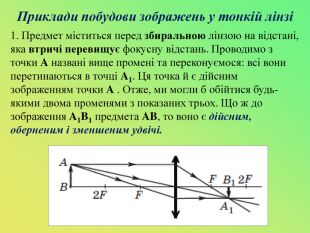
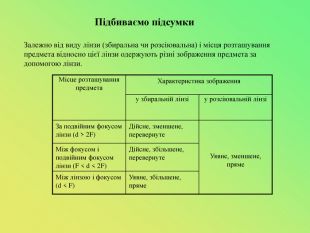
Презентація до уроку "Лінзи. Оптична сила і фокусна відстань лінзи.Побудова зображень,що дає тонка лінза."
Про матеріал
Презентація до уроку який був проведенний в рамках "Тиждень фізики в гімназії".
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку