Презентація. Коло, вписане в трикутник
Про матеріал
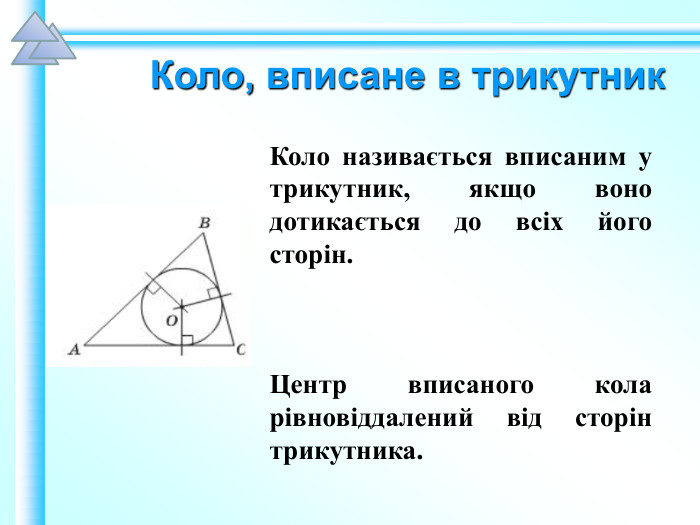
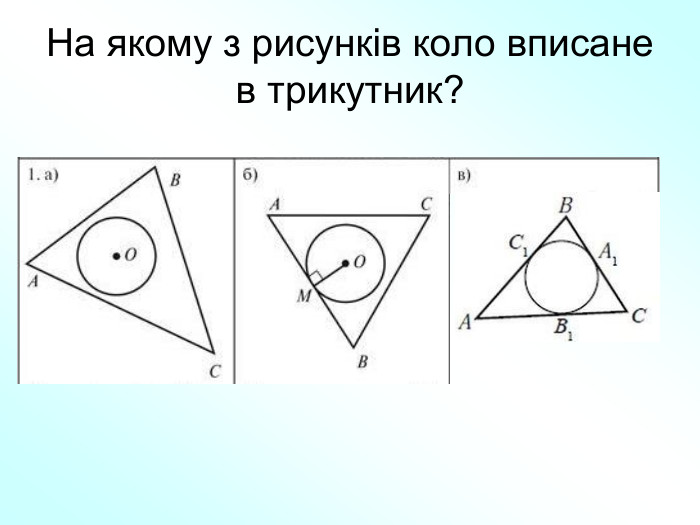
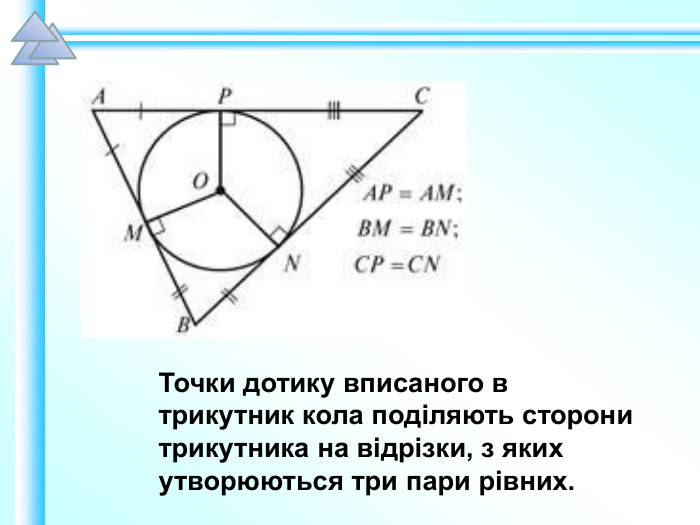
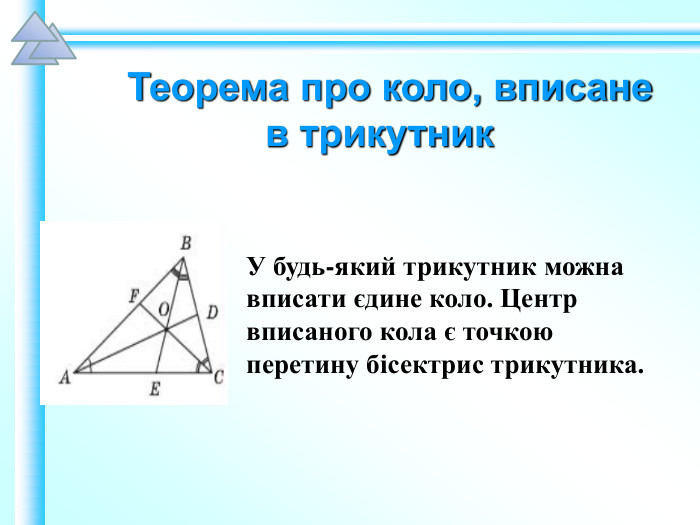
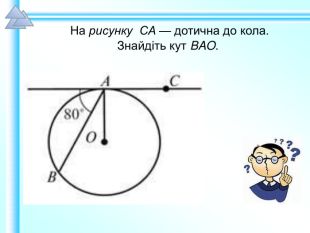
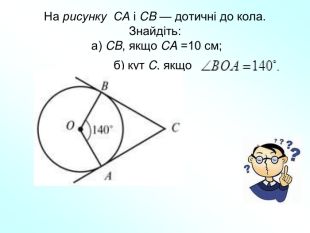
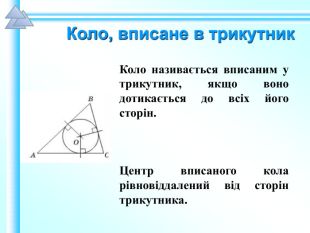
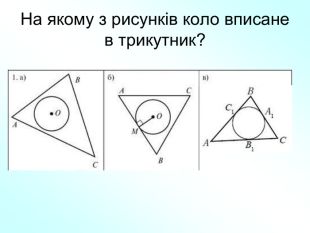
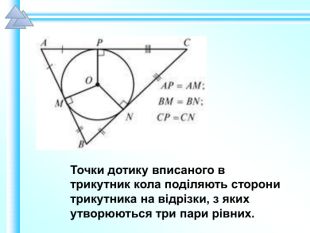
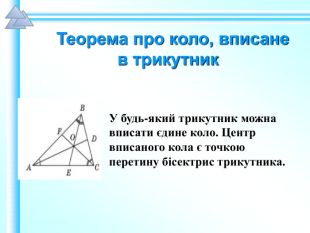
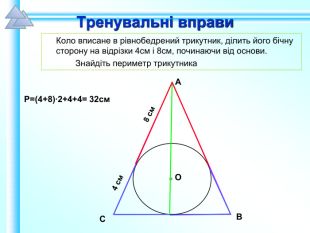
Матеріали презентації "Коло, вписане в трикутник" приведені у відповідність до п. 23.2 підручника "Геометрія. 7 клас. (Єршова, Голобородько)". Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку