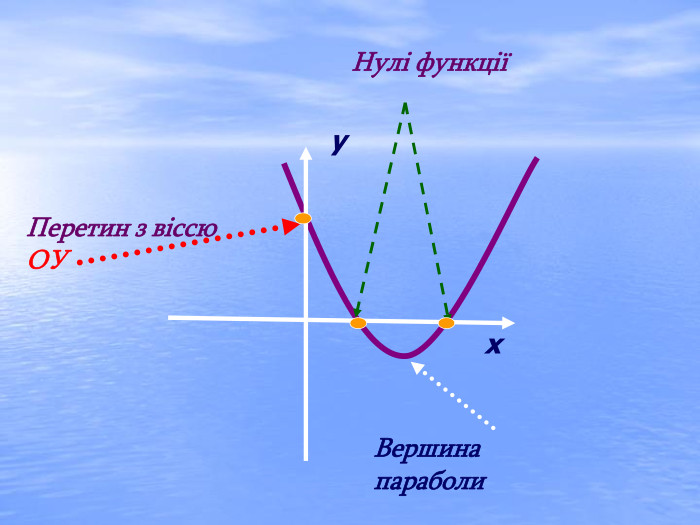
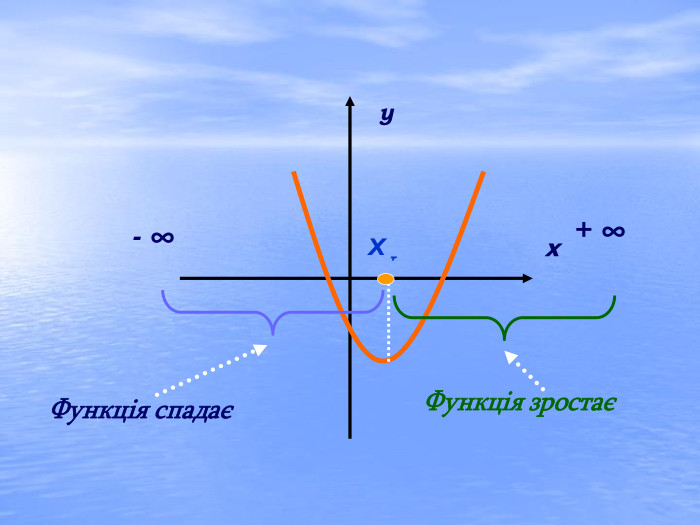
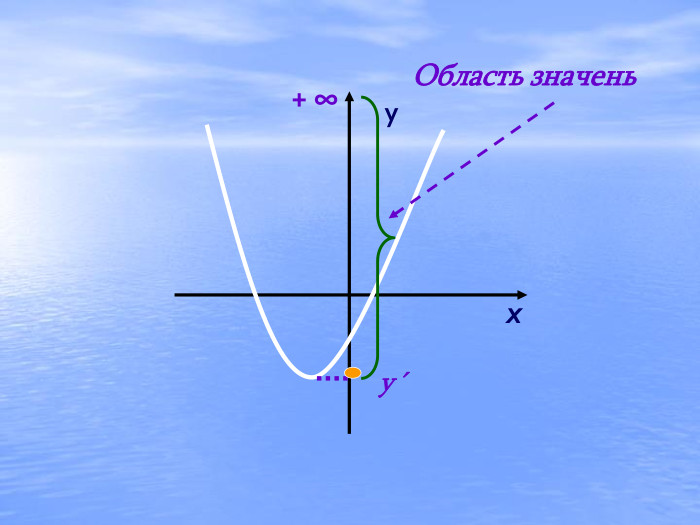
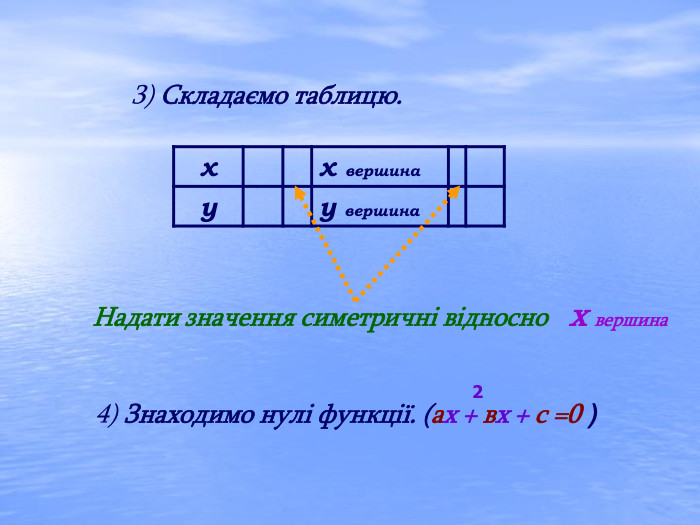
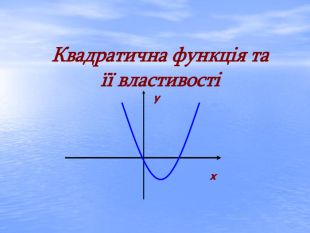
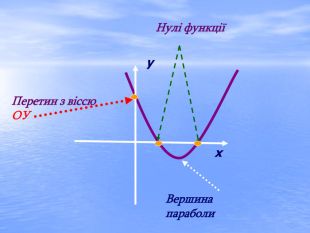
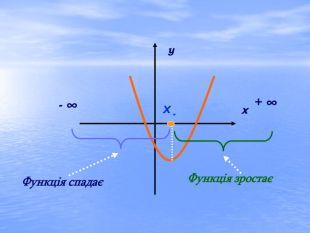
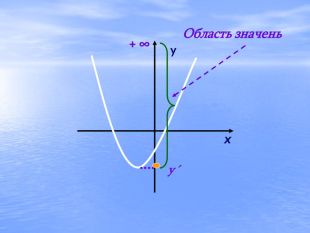
Презентація "Квадратична функція та її властивості"
Про матеріал
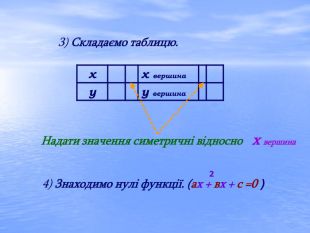
Матеріали презентації "Квадратична функція та її властивості" можна використати на уроках алгебри 9 класу. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку