Презентація "Лінійна функція"
Про матеріал
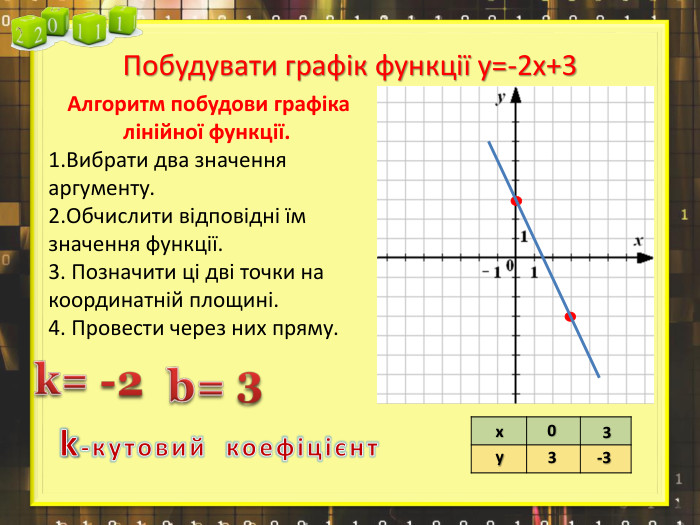
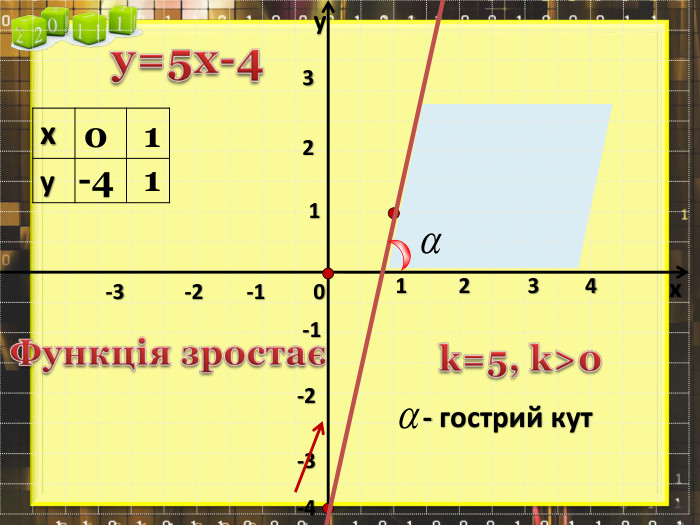
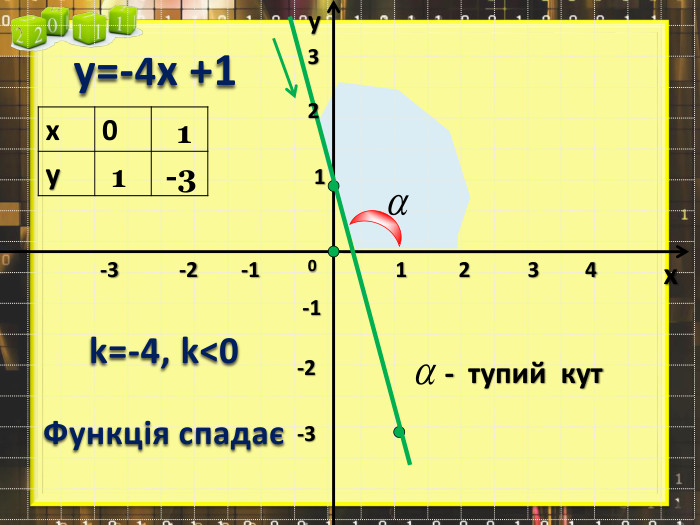
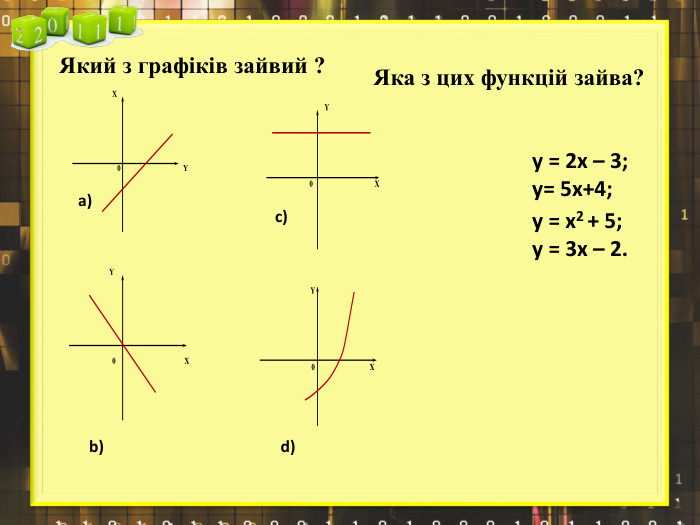
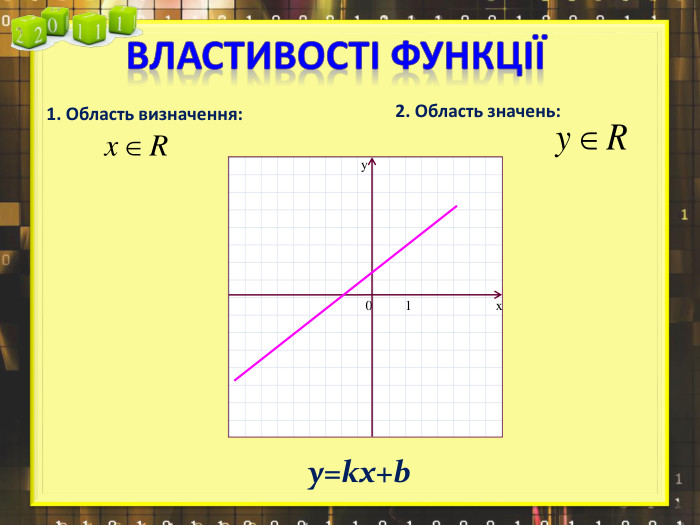
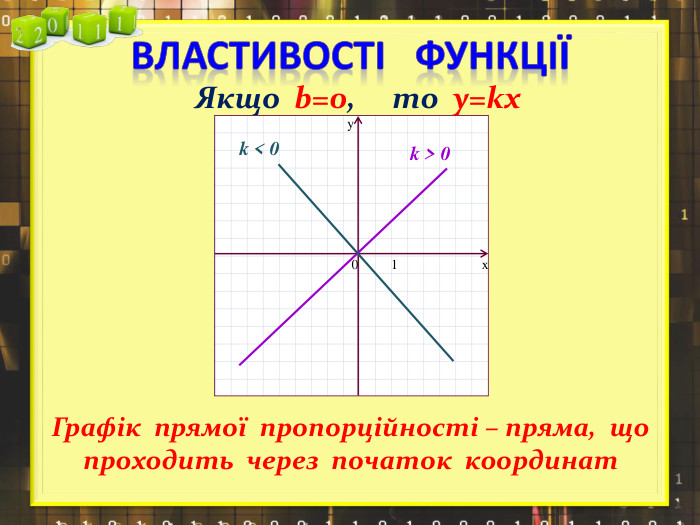
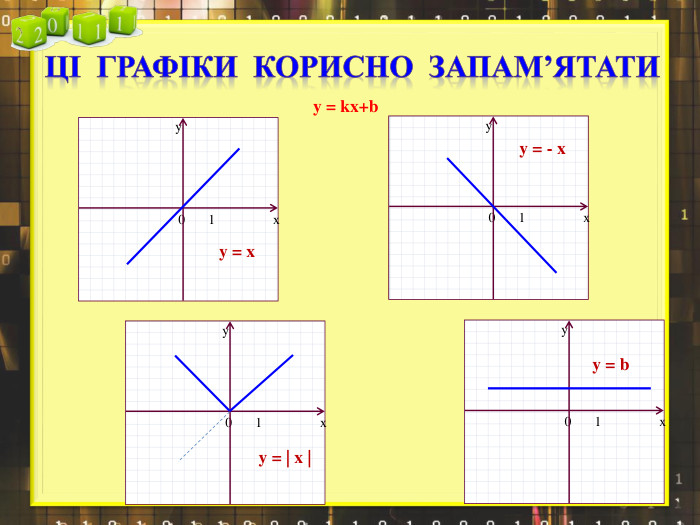
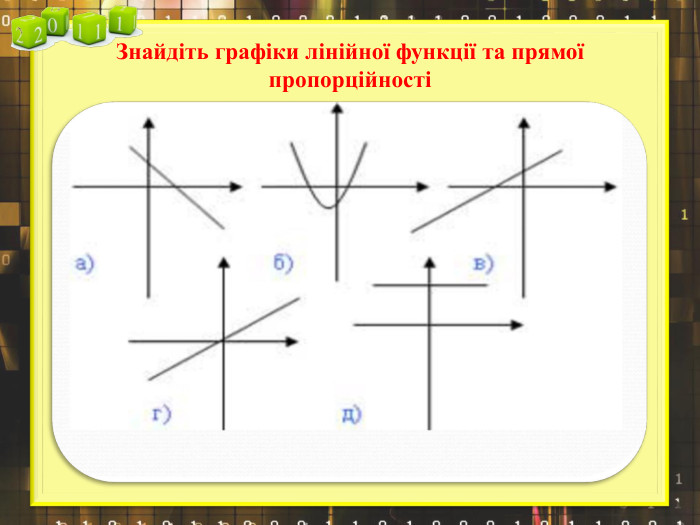
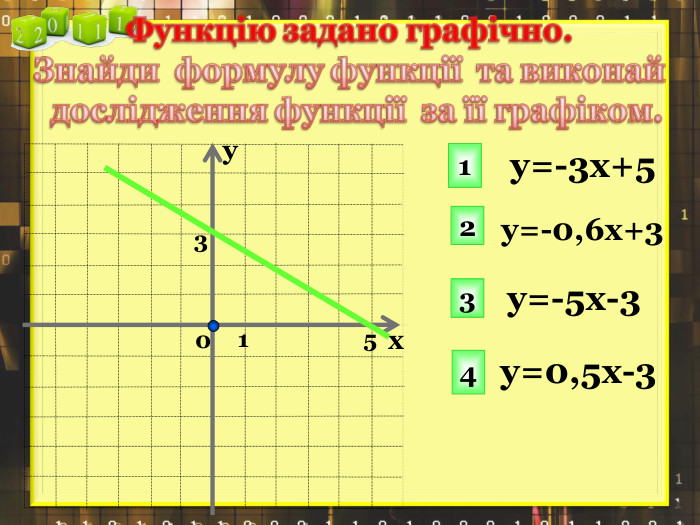
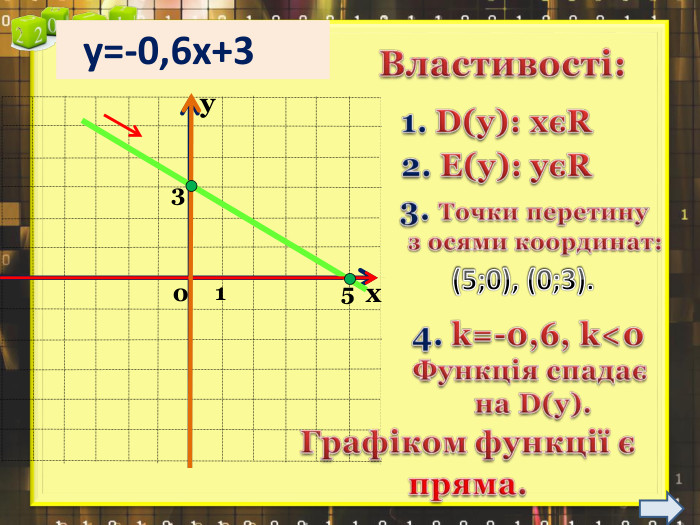
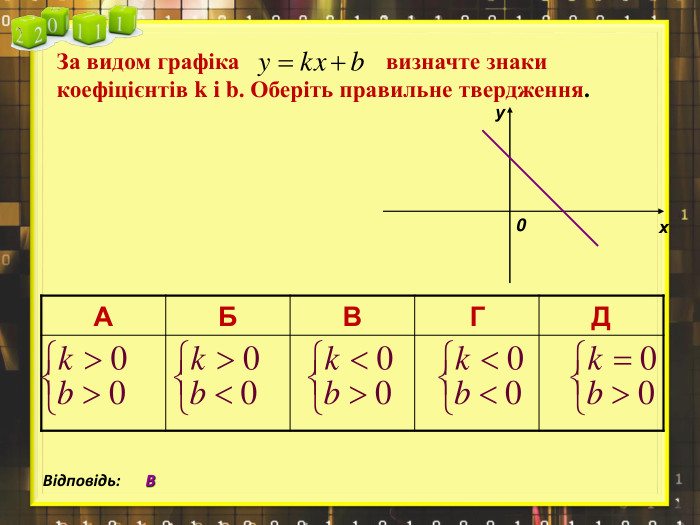
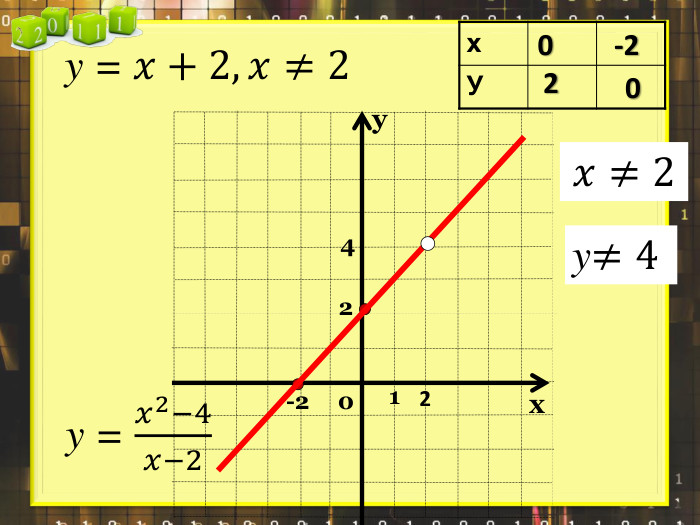
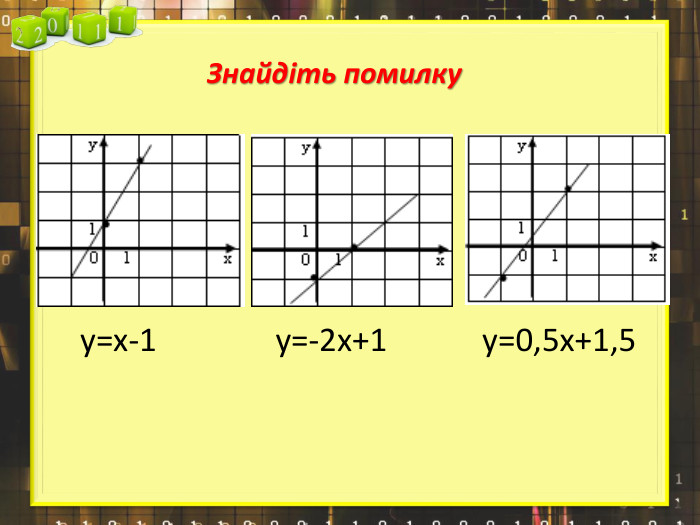
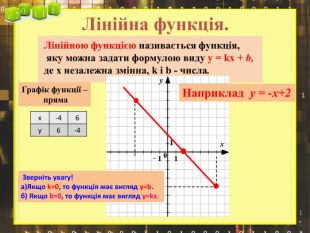
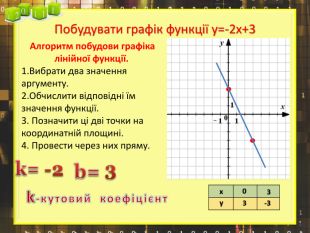
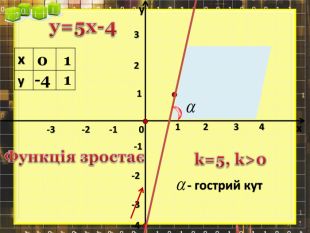
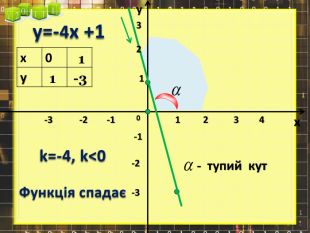
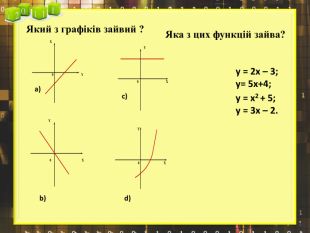
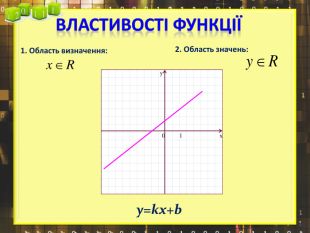
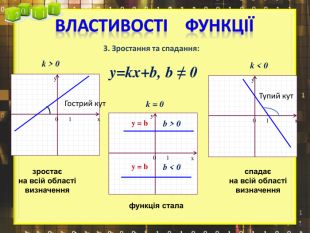
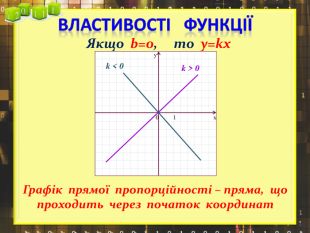
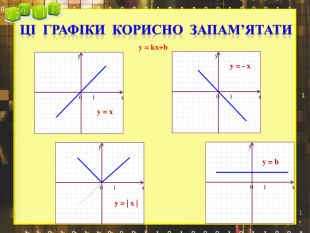
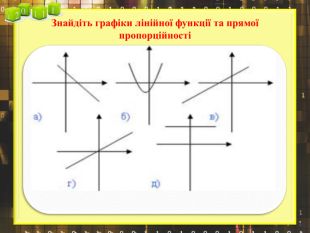
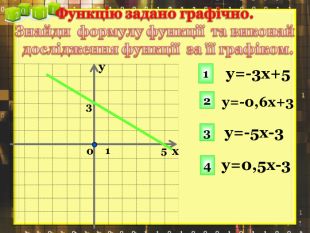
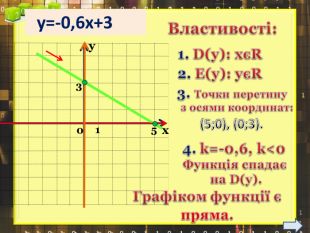
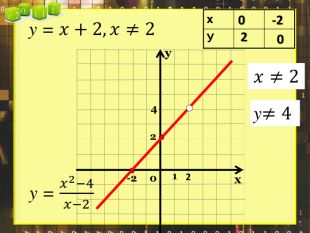
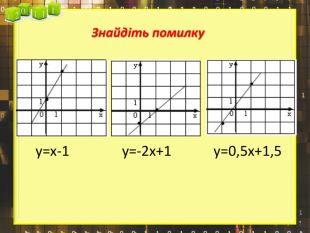
Ввести означення лінійної функції, сформулювати її властивості, навчитися будувати графіки лінійної функції.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку