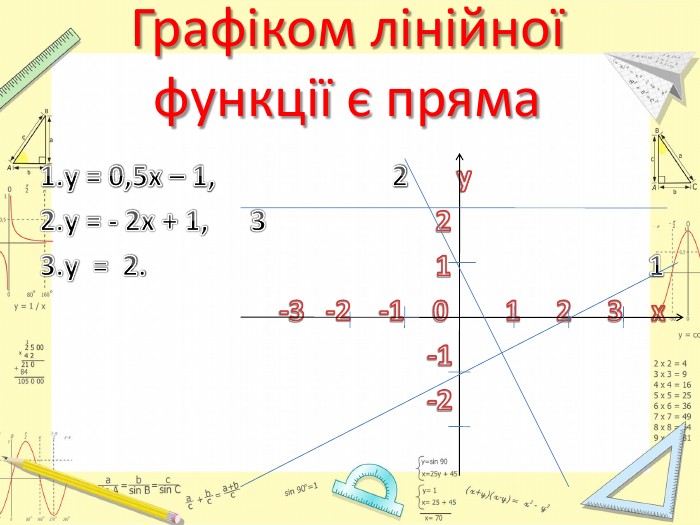
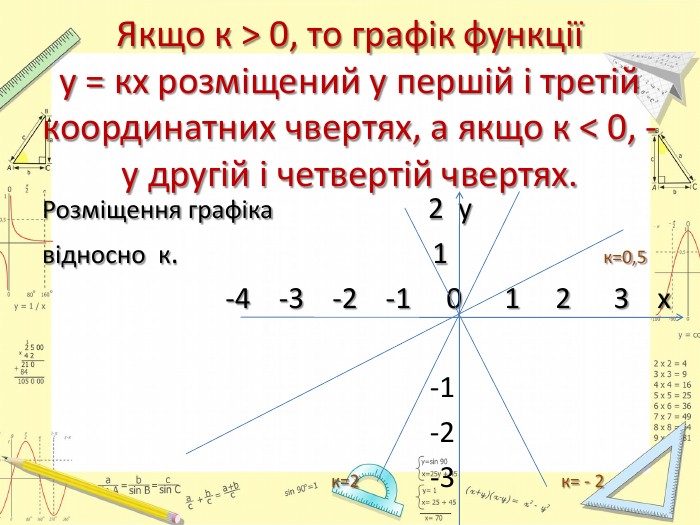
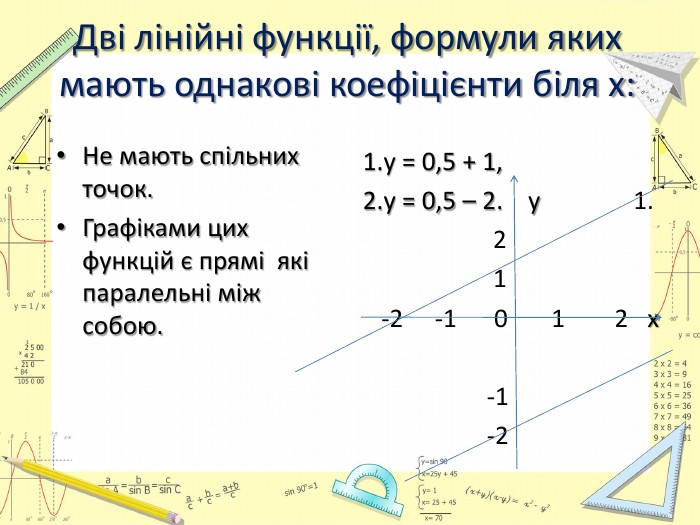
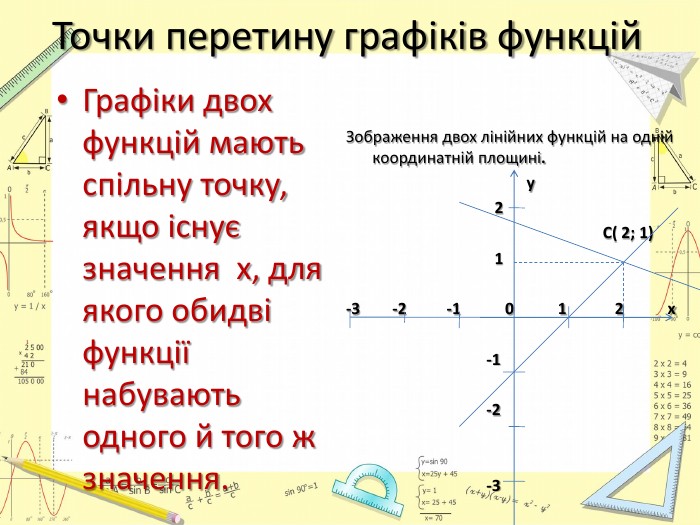
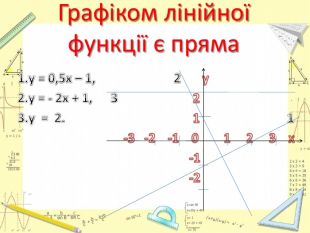
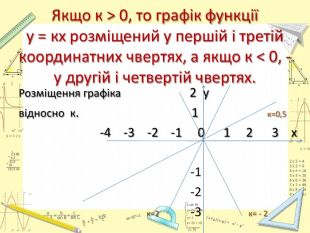
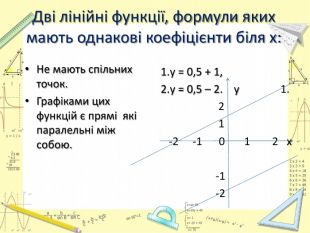
Презентація "Лінійна функція. Графік і властивості функції"
Про матеріал
Тема "Лінійна функція. Графік і властивості лінійної функції" розрахована на повторення, узагальнення та систематизації знань. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку