Презентація "Логарифмічні рівняння"

Логарифмічні рівнянняалгебра. 11 клас

Мета уроку:навчальна: узагальнити та систематизувати знання учнів про логарифмічні рівняння та способи їх розв’язання, формувати вміння і навички розв’язувати логарифмічні рівняння, користуючись означенням та властивостями логарифма;розвивальна: удосконалювати навички застосовувати властивості логарифмів під час розв’язування рівнянь, удосконалювати розумові здібності, здатності до самостійного мислення, розвивати пам’ять, увагу;виховна: формувати працьовитість, прищеплювати бажання мати якісні, глибокі знання, виховувати культуру математичних записів та інтерес до вивчення предмету.

1. Які рівняння називаються логарифмічними?Логарифмічні рівняння містять невідому величину під знаком логарифма або в основі логарифма. Приклади логарифмічних рівнянь:log3𝑥=4; log𝑥3+log3𝑥=4; log3log4𝑥=0 

2. Які основні способи розв'язування логарифмічних рівнянь?за означенням логарифма;за основною логарифмічною тотожністю;методом потенціювання;методом логарифмування;переходом до іншої основи;методом заміни змінної. Особливу увагу при розв’язуванні логарифмічних рівнянь слід звернути на виконання обмежень, які накладає логарифм, тобто виконання відповідних нерівностей, або області визначення. 

Завдання з вибором однієї правильної відповіді

№ 20, 2017д1. Якому проміжку належить корінь рівняння 𝐥𝐨𝐠𝟐𝒙=𝟐𝐥𝐨𝐠𝟐𝟑? {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД(0; 2](2; 4](4; 6](6; 8](8; 10]

Відповідь: ДРозв’язання.log2𝑥=2log23;ОДЗ 𝑥>0;log2𝑥=log232;𝑥=9. Число 9 належить проміжку 8;10. 

№ 16, 2010_ІІ2. Якому з наведених проміжків належить корінь рівняння 𝐥𝐨𝐠𝟑𝒙=𝟐? {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД(–4; –1](–1; 2](2; 5](5; 8](8; 11]

Відповідь: ДРозв’язання.log3𝑥=2;ОДЗ 𝑥>0;log3𝑥=2log33;log3𝑥=log39;𝑥=9. Число 9 належить проміжку(8;11]. 

Завдання відкритої форми з короткою відповіддю

№ 29, 20143. Розв’яжіть рівняння𝐥𝐨𝐠𝟎,𝟒𝟓𝒙𝟐−𝟖=𝐥𝐨𝐠𝟎,𝟒(−𝟑𝒙). Якщо рівняння має один корінь, запишіть його у відповіді. Якщо рівняння має кілька коренів, запишіть у відповіді їхню суму. 

Розв’язання.log0,45𝑥2−8=log0,4(−3𝑥);5𝑥2−8=−3𝑥,5𝑥2−8>0; або 5𝑥2−8=−3𝑥,−3𝑥>0. Вибір відповідної системи пов’язаний з тим, яку з нерівностей, легше розв'язати. Таким чином, маємо: 5𝑥2+3𝑥−8=0,𝑥<0. Отже, 𝑥=1,𝑥=−1,6,𝑥<0. Відповідь: -1,6. 

№ 25, 20094. Розв’яжіть рівняння𝐥𝐨𝐠𝟔𝒙−𝟑+𝐥𝐨𝐠𝟔(𝒙−𝟖)=𝟐. Якщо рівняння має один корінь, то запишіть його у відповідь; якщо воно має два корені, то у відповідь запишіть їх суму. 

Розв’язання.log6𝑥−3+log6𝑥−8=2. Дане рівняння рівносильне системіlog6𝑥−3𝑥−8=2,𝑥−3>0,𝑥−8>0. Звідси 𝑥−3𝑥−8=62,𝑥−8>0; 𝑥2−11𝑥−12=0,𝑥>8. Отже, 𝑥=−1,𝑥=12,𝑥>8. Відповідь: 12. 

№ 30, 2015_І5. Розв’яжіть рівняння𝐥𝐨𝐠𝟓𝟐𝒙+𝐥𝐨𝐠𝟓𝒙=𝟐. Якщо рівняння має один корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то у відповіді запишіть їхню суму. Якщо рівняння не має коренів, запишіть у відповіді число 100. 

Розв’язання.log52𝑥+log5𝑥=2;ОДЗ 𝑥>0. Нехай log5𝑥=𝑡. Тоді рівняння набере вигляду: 𝑡2+𝑡−2=0;Отже, 𝑡=−2,𝑡=1. Маємо: log5𝑥=−2,log5𝑥=1;𝑥=125,𝑥=5. Отже, 125+5=5125=5,04 Відповідь: 5,04. 

№ 30, 2015_ІІ6. Розв’яжіть рівняння𝐥𝐨𝐠𝟒𝒙∙𝐥𝐨𝐠𝟒𝒙+𝐥𝐨𝐠𝟒𝟏𝟏𝟔=𝟑. Якщо рівняння має єдиний корінь, то запишіть його у відповіді, якщо рівняння має кілька коренів, то запишіть у відповіді їхню суму. Якщо рівняння не має коренів, запишіть у відповіді число 100. 

Розв’язання.log4𝑥∙log4𝑥+log4116=3;ОДЗ 𝑥>0.log4𝑥∙log4𝑥+log44−2=3;log4𝑥∙log4𝑥−2log44=3;log4𝑥∙log4𝑥−2=3;log42𝑥−2log4𝑥−3=0.  

Нехай log4𝑥=𝑡. Тоді рівняння набере вигляду 𝑡2−2𝑡−3=0;Отже, 𝑡=−1,𝑡=3. Маємо: log4𝑥=−1,log4𝑥=3;𝑥=14,𝑥=64. Отже, 14+64=6414=64,25 Відповідь: 64,25. 

Завдання відкритої форми з розгорнутою відповіддю

№ 30, 2015_ІІ7. Знайдіть значення параметра а, при якому корінь рівняння 𝐥𝐠𝒔𝒊𝒏𝟓𝝅𝒙=𝟏𝟔+𝒂−𝒙 належить проміжку 32;2 8. Знайдіть найменше ціле значення параметра а, при якому рівняння𝐥𝐨𝐠𝟖(𝒙+𝟐)=𝐥𝐨𝐠𝟖(𝟐𝒙−𝒂) має корені. № 32, 2007

Самостійна робота

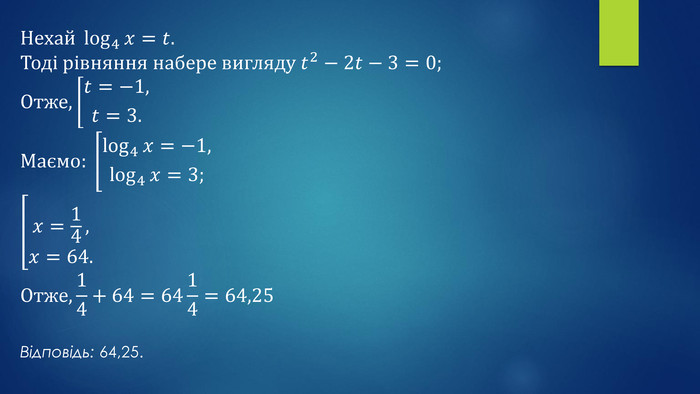
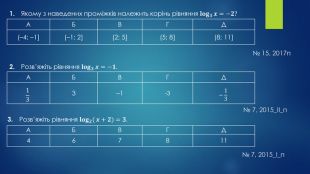
№ 15, 2017п1. Якому з наведених проміжків належить корінь рівняння 𝐥𝐨𝐠𝟑𝒙=−𝟐? {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД(–4; –1](–1; 2](2; 5](5; 8](8; 11]2. Розв’яжіть рівняння 𝐥𝐨𝐠𝟑𝒙=−𝟏. {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД133–1-3−13{2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД3–1-3№ 7, 2015_ІІ_п3. Розв’яжіть рівняння 𝐥𝐨𝐠𝟐(𝒙+𝟐)=𝟑. {2 D5 ABB26-0587-4 C30-8999-92 F81 FD0307 C}АБВГД467811№ 7, 2015_І_п

4. Розв’яжіть рівняння 𝐥𝐨𝐠𝟐𝒙+𝐥𝐨𝐠𝟐𝒙−𝟕=𝟑. Якщо рівняння має єдиний корінь, то запишіть його у відповіді. Якщо рівняння має кілька коренів, то запишіть у відповіді їхню суму. № 28, 2016п5*. Розв'яжіть рівняння 𝟑𝐥𝐠𝒙+𝟏−𝐥𝐠𝒙−𝟑=𝟐. Якщо рівняння має один корінь, то запишіть його у відповідь. Якщо рівняння має більше одного кореня, то у відповідь запишіть суму всіх коренів. № 35, 2010_ІІ_п