ТЕМА : Методологічні знання з лінійної алгебри

Презентація студентки 1 курсу групи ММЗСО

Тюпи Олени

Лінійна алгебра

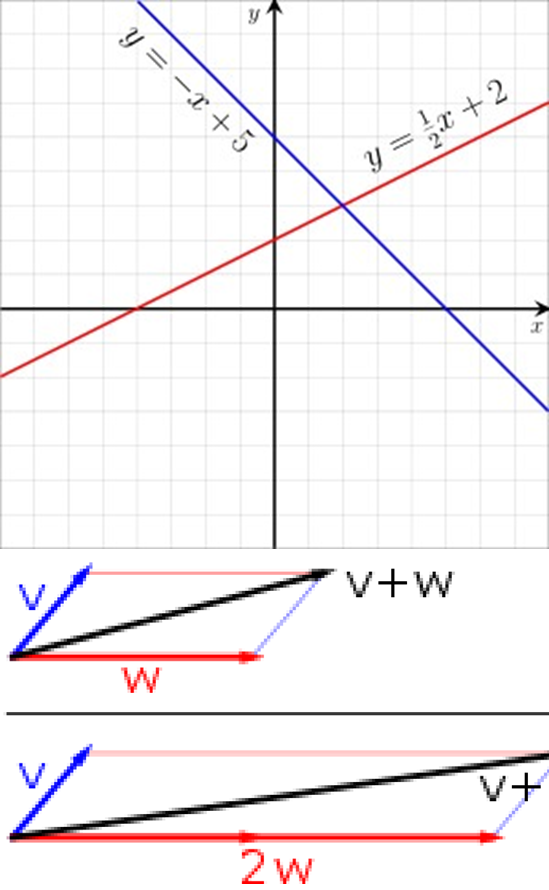Насам перед що таке лінійна алгебра?

Це така частина алгебри, що вивчає вектори, векторні простори, лінійні відображення та системи лінійних рівнянь.

До лінійної алгебри відносять: теорію лінійних рівнянь, теорію визначників, теорію матриць, теорію векторних просторів та лінійних

перетворень у них, теорію форм (наприклад, квадратичних), теорію інваріантів (частково), тензорне числення (частково).

Історія

Історично першим питанням лінійної алгебри було знаходження розв'язків лінійних рівнянь.

Побудова теорії для систем таких рівнянь потребувала таких інструментів, як теорія

матриць і визначників, і привела до появи теорії векторних просторів.

Лінійні рівняння як рівняння прямих і площин стали природним предметом вивчення після винаходу

Декартом і Ферма методу координат (близько 1636).

Гамільтон у своїй роботі 1833 представляв комплексні числа у вигляді, як ми б зараз сказали, двовимірного

дійсного векторного простору, йому належить відкриття кватерніонів, а також авторство терміну «вектор». .

Теорія матриць була розроблена у працях Келі (1850-ті). Системи лінійних рівнянь у векторному для матриці вигляді вперше з'явилися, мабуть, у роботах Лагерра

(1867). Герман Грассман у роботах 1844 та 1862 року вивчає те, що ми тепер назвали б алгеброю, і його формальний виклад по суті є першою аксіоматичною теорією систем алгебри. У явному вигляді аксіоми лінійного простору

сформульовані в роботі Пеано (1888)

Основні поняття

Розвиток лінійної алгебри почався з практичних задач розв'язування лінійних рівнянь та аналітичної геометрії. Поступово сформувалися абстрактні поняття

вектора, матриці, векторного простору, скалярного добутку, визначників тощо.

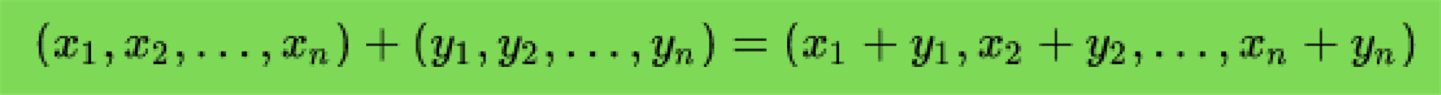
Вектор у лінійній алгебрі є узагальненням геометричного тривимірного вектора, що використовується в геометрії та механіці. У розумінні лінійної алгебри вектор — це індексована сукупність чисел або інших математичних об'єктів (Х1,Х2......Хn), яка має ту властивість, що її можна множити на число.

Компонентами векторів є зазвичай дійсні числа, хоча вони можуть бути іншими математичними об'єктами, наприклад, комплексними числами, векторами або матрицями.

Важливо тільки, щоб для них була визначена операція додавання. Аналогічно, число, на яке можна помножити вектор, зазвичай є дійсним числом, але може бути й комплексним, головне, щоб для вектора була визначена операція множення на нього.

Векторний простір

Векторним або лінійним простором називають множину векторів, до якої належать вектори з будь-яким можливим значенням компонент, тобто це множина всіх векторів заданої

природи. Окрім того, що у векторному просторі визначені операції додавання векторів та

множення на скаляр (число), для того щоб множина векторів складала векторний простір на ній повинен діяти ряд аксіом: комутативності, асоціативності, дистрибутивності додавання і множення на скаляр, існування нульового і протилежного елемента.

Число n, яке визначає кількість елементів вектора називається розмірністю векторного простору. Лінійна алгебра вивчає векторні простори скінченної розмірності. Вектори з нескінченним числом компонент вивчаються іншими розділами математики, зокрема функціональним аналізом.

Лінійне відображення

Між двома векторними просторами можна задати відображення. Лінійна алгебра вивчає

відображення, які називаються лінійними. Лінійне відображення пов'язує між собою два векторні

простори, побудовані над одним і тим же полем, тобто числа, на які множаться вектори повинні

мати однакову природу. Воно є гомоморфізмом,

тобто кожному елементу однієї множини лінійне відображення ставить у відповідність елемент

іншої множини, крім того, воно має ту властивість, що сумі елементів однієї множини відповідає сума відповідних елементів іншої множини, і елементу, помноженому на число, відповідає елемент іншої множини, помножений на те ж число.

Лінійне відображення простору у себе

(ендоморфізм) називається лінійним перетворенням.

що має властивість лінійності:

Лінійне відображення зберігає операції додавання векторів і множення вектора на скаляр:

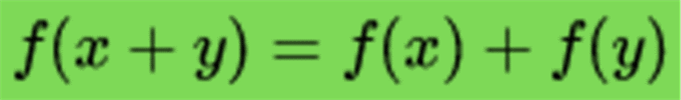
адитивність

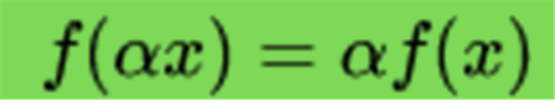
однорідність

Матриця

Докладніше: Матриця (математика)

Найважливішим способом задання лінійного відображення є матриця — таблиця чисел або інших математичних об'єктів з двома індексами, наприклад       . За допомогою матриці лінійне відображення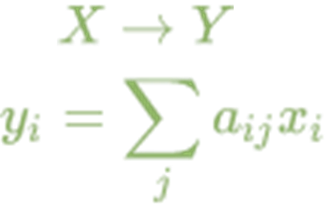                    задається у вигляді

тобто кожна компонента вектора y з векторного простору Y є лінійною комбінацією компонент вектора xз векторного простору X з коефіцієнтами, які визнаються елементами матриці A.

У випадку лінійного перетворення матриця перетворення квадратна.

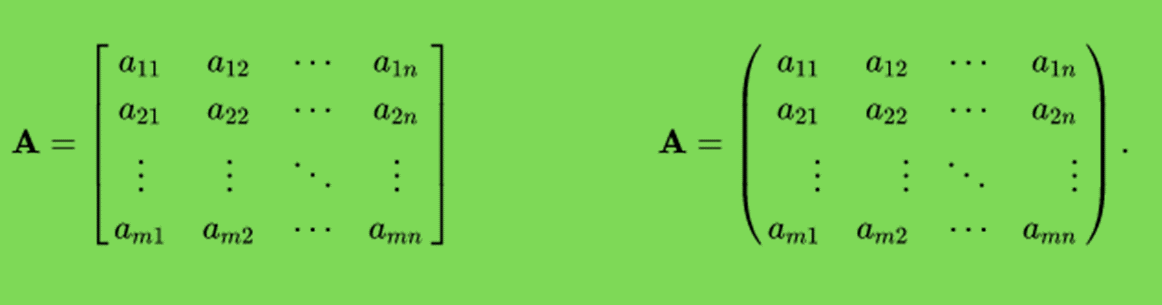
Система лінійних алгебраїчних рівнянь

Задача знаходження елемента векторного простору, який при лінійному перетворенні переходить у визначений елемент іншого векторного простору приводить до поняття системи лінійних алгебраїчних рівнянь.

Система m лінійних алгебраїчних рівнянь з n невідомими — це система рівнянь виду

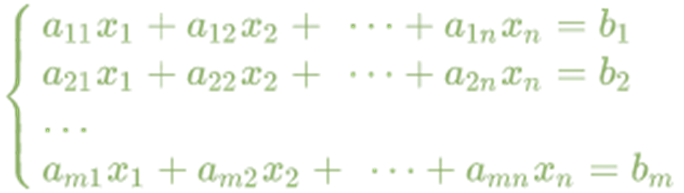
Вона може бути представлена у матричній формі як:

або:

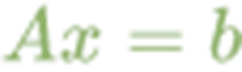
Висновок

До  методологічних  знань  конкретно  наукового  рівня належать  знання  про: предмет навчальної дисципліни; конкретно наукові методи навчальної дисципліни; фундаментальні поняття;

фундаментальні відношення між поняттями; фундаментальні теоретичні факти (означення, аксіоми,

теореми); зв'язок з іншими навчальними дисциплінами; межі застосовності знань; історію розвитку.

Формування методологічних знань не може відбуватися відірвано від формування предметних знань, а тому важливим фактором є кількість кредитів (і відповідно годин), передбачених на вивчення навчального предмету.

Предметом вивчення лінійної алгебри є, в основному, лiнiйнi скінченновимірні простори та лiнiйнi вiдображення в цих просторах. Основними методами дослідження є матричний та векторний методи.

Крім названих методів, курс лінійної алгебри має у своєму арсеналі чимало конкретно наукових методів.

Наприклад, під час вивчення розділу «Системи лінійних рівнянь» розглядаються метод Гауса, метод

Жордана-Гауса, метод Крамера, метод оберненої матриці (матричний метод). Для зведення квадратичних форм до суми квадратів використовуються метод Лагранжа, метод Якобі. Знайшов своє

явне відображення під час вивчення цього курсу аксіоматичний метод. Лінійна алгебра, абстрагуючись

від сутності об’єктів, на перше місце висуває операції , задані на об’єктах, і властивості цих операцій. Так, розглядаючи лінійний простір Х ми абстрагуємося від природи об’єктів множини Х (це можуть бути числа, n- вимірні вектори, матриці, функції тощо), головне – це алгебраїчні операції над об’єктами цієї множини та їх властивості, описані в аксіомах лінійного простору. 

Література

1.Н. В. Кугай - РОЗШИРЕННЯ ДОСВІДУ ПІЗНАННЯ СТУДЕНТІВ У ПРОЦЕСІ НАВЧАННЯ ЛІНІЙНОЇ АЛГЕБРИ

2.ЛІНІЙНА АЛГЕБРА ТА АНАЛІТИЧНА ГЕОМЕТРІЯ , В. В. Булдигін, І. В.

Алєксєєва, В. О. Гайдей, О. О. Диховичний, Н. Р. Коновалова, Л. Б. Федорова

3.https://uk.wikipedia.org/wiki/%D0%9B%D1%96%D0%BD%D1%96%D0%B9%D0

%BD%D0%B0_%D0%B0%D0%BB%D0%B3%D0%B5%D0%B1%D1%80%D0%B0