Презентація " Міжпредметні звязки фізики і математики"
Про матеріал
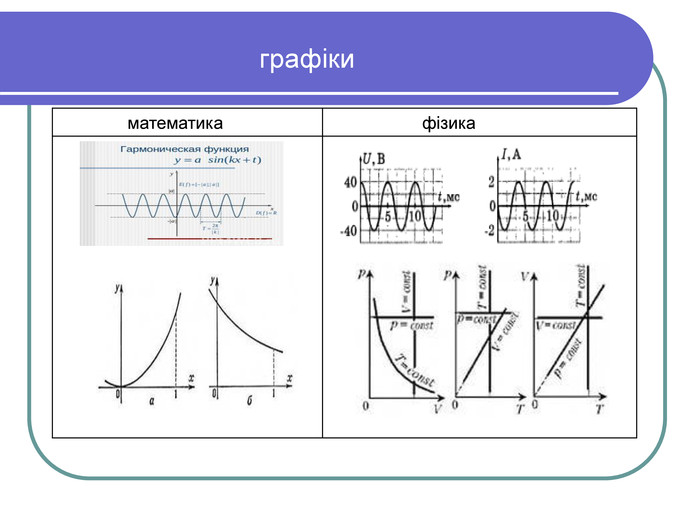
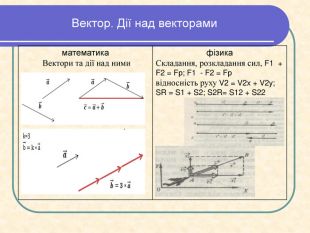
В прєзентації розглядаються види міжпредметних звязків та їх прояви і проблемні ситуації в яких вони застосовуються під час вивчення окремих розділів і тем
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку