Презентація. "Многочлени. Повторення вивченого"
Про матеріал
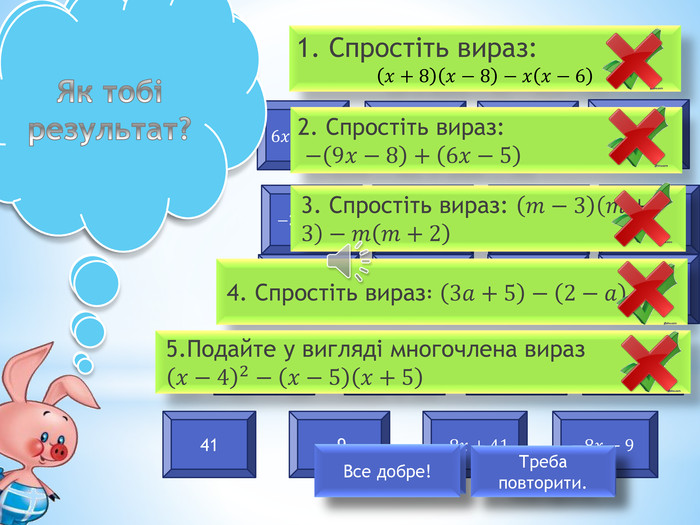
Інтерактивна презентація для самостійного повторення учнями матеріалу з теми "Многочлени"
Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
До підручника
Алгебра 7 клас (Тарасенкова Н.А., Богатирьова І.М., Коломієць О.М., Сердюк 3.0.)
До уроку
Повторення Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
























-

Нікітенко Катерина Аркадіївна
08.09.2024 в 12:51
Дякую! Мирного неба!
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

САБУРОВА ВАЛЕНТИНА
03.01.2023 в 18:00
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Самікова Ірина Олександрівна
30.12.2022 в 19:11
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Константинова Олена Павлівна
01.09.2022 в 18:49
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Любчак Ольга Анатоліївна
09.05.2022 в 16:38
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
Показати ще 2 відгука