Презентація на тему "Паралельні прямі в просторі"
Про матеріал
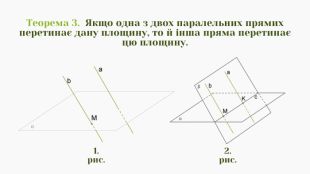
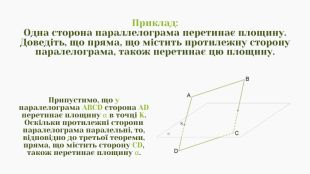
Презентація з теми "Паралельні прямі в просторі" на уроках геометрії у 11 класі. Призначена для практичного використання в умовах дистанційного навчання. Матеріали допоможуть вчителю раціонально використати свій час при перевірці домашнього завдання і проведенні класної роботи. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку