Презентація на тему: "Прогресії 9 клас"

Прогресії. 9 клас. Алгебра. Анотація: Пропонований матеріал призначений для вчителів, які працюють у 9 класі за новою програмою «Математика 5-9класи. Програма для загальноосвітніх навчальних закладів. Київ. Ірпінь. 2012». Робота містить презентацію, яка може бути використана при вивченні теми «Числові послідовності». Тип ресурсу: Презентації Автор(и): Корнієнко Н.А. Галузь освіти: Загальна освіта -> Математика Аудиторія: Учителі, учні Рік видання ресурсу: 2018 Кількість сторінок: 63 Джерело: «Загальноосвітня школа І-ІІІ ступенів №3 » м. Вовчанськ Мова ресурсу: українська Цінність ресурсу: 5

Прогресії навколо нас 9 клас Алгебра Розробила вчитель математики “ЗОШ №3 ” м. Вовчанська Корнієнко Наталя Анатоліївна

найціннішим є використання набутих знань у життєвих ситуаціях.

Історичні відомості про прогресії

Слово “прогресія” походить від латинського слова “progressio” і означає “рух уперед” (як і слово “прогрес”). Уперше цей термін як математичний вживається у працях римського вченого Боеція (V - VIст.).

Прогресії як часткові види числових послідовностей, трапляються в папірусах ІІ тисячоліття до н. е.

АНГЛІЯ XVIII століття В XVIII ст. в англійських підручниках з’явилися позначення арифметичної і геометричної прогресії. Арифметична Геометрична

Найдавнішою задачею, пов’язаною з прогресіями, вважають задачу з єгипетського папірусу Ахмеса: “Нехай тобі сказали: розділи десять мір ячменю між 10 чоловіками так, щоб різниця між кожним чоловіком і його сусідом становила 1/8 міри ячменю ”.

У папірусі подається не тільки текст задачі, але й пропонується правило для обчислення частки першої з десяти осіб.

Задача із папірусу Рінда “Є 7 будинків, в кожному будинку по 7 котів, кожен кіт з’їдає 7 мишей, кожна миша з’їдає по 7 колосків ячменю, кожен колосок, якщо посіяти зерно з нього, дає 7 мір ячменю. Знайти суму загального числа будинків, котів, мишей, колосків і мір”.

Ця стародавня задача на геометричну прогресію не раз зустрічається в різних народів з дещо зміненим текстом. Зустрічається вона і серед древньоруських народних задач. “ Іде 7 баб; у кожної баби по 7 палиць; на кожній палиці по 7 сучків; на кожному сучку по 7 кошиків; у кожному кошику по 7 горобців, у кожного горобці по 7 зерин . Скільки всього предметів?”

З досліджень вавилонських клинописних текстів епохи Хаммурані (XVIII cт. до н. е.) бачимо, що і в стародавньому Вавилоні розв’язування деяких питань господарського і наукового характеру приводимо до арифметичної і геометричної прогресії.

Ось одна з таких задач “10 братів; 1 2/3 міни срібла; брат над братом піднімається; на скільки піднімається, я не знаю. Частка восьмого 6 мехелів. Брат над братом на скільки піднімається?” (1 2/3 міни становлять 100 мехелів).

У Стародавній Греції в часи Евкліда і Архімеда (ІІІ ст. до н. е.) властивості прогресій розглядались у зв’язку з теоретичними дослідженнями. Так, у книзі Евкліда “Начала” подається формула суми трьох членів геометричної прогресії.

У нас задачі на прогресії вперше зустрічаються в одній з найдавніших пам’яток руського права, в “Руській правді”, складеній при Ярославі Мудрому в ХІ столітті.

Там є стаття, присвячена обчисленню приплоду від 22 овець за 12 років, при умові, що кожна вівця щорічно приносить одну овечку і одного барана.

Значна кількість задач на прогресії міститься в чудовій пам’ятці математичної літератури початку XVIII cт. “Арифметиці” Л. П. Магніцького.

Зі знаходженням суми членів арифметичної прогресії пов’язана така цікава історія. Відомий німецький математик Карл Гаусс (1777 - 1875) ще у школі виявив блискучі математичні здібності. Якось учитель запропонував учням знайти суму перших ста натуральних чисел. Маленький Гаусс розв’язав цю задачу за хвилину. Зміркувавши, що суми 1+100, 2+99 і т. д. рівні, він помножив 101 на 50, тобто число таких сум. Інакше кажучи, він помітив закономірність, яка властива арифметичній прогресії.

Складемо послідовність чисел 1, 2, 4, 8, 16 … Дана послідовність є геометричною b1 = 1, q = 2, n = 64. S64 - ? Загальна кількість зерен, яку попросив винахідник, дорівнює S64=264-1

Багатий раджа був приголомшений, коли дізнався, що він не в змозі задовольнити це “скромне” бажання. Справа в тому, що значення виразу 264-1 дорівнює 18446744073709551615. Для того, щоб зрозуміти, наскільки величезним є це число, уявимо, що зерно зберігають у коморі площею 12 га. Її висота була б більшою за відстань від Землі до Сонця.

Означення і властивості (аn)-арифм. прогресія аn+1 = аn + d; (аn)-n-й член арифметичної прогресії є середнім арифметич- ним двох сусідніх з ним членів. аn = Якщо (аn)- скінченна арифметич- на прогресія, то Будь-яка арифм. прогресія (аn) може бути записана формулою аn = kn+b, де k i b – числа. (вn)-геометр.прогресія вn+1 = вn . q (вn)- n-й член геометричної прогресії є середнім геометрич- ним двох сусідніх з ним членів. вn = Якщо (вn)- скінченна геометрична прогресія, то

Формула n-го члена арифметичної та геометричної прогресії та їх суми (аn)-арифм. прогресія аn = а1 + d (n – 1). (аn)- арифм. прогресія Sn = n; Sn = (вn) - геометр.прогресія bn = b1 . qn-1; (вn) - геометр.прогресія 1) 2) 3)

Усні вправи 1. Відгадати число: 55 59 63 ?

Обчислити: 33 – 7 = (22 + 6) . 22 = 24 . 5 = 23 . 20 = 25 . 10 = (20 + 210) – 404 = Яку залежність ви побачили? Усні вправи

Знайди помилку. 1) аn = 2n + 1; 6) Sn = . n; 2) хn= n2 – 8n; 7) xn+1 = xn + d; 3) bn = b1 + d . (n – 1); 8) Sn = ; 4) an = a1 + 8d; 9) yn = 2n; 5) cn = c1 . qn-1; 10) zn = n2. Назвати номер неправильної формули, якщо така є. Усні вправи

Чи будуть всі написані послідовності арифметичними прогресіями? 5, 7, 9, 11, … 20, 10, 0 , -10, … 2, 4, 6, 8, … 1, 2, 6, 8, … 15, 3, -9, … Вказати номер послідовності, яка не є арифметичною прогресією. Усні вправи

Чи будуть всі написані послідовності геометричними прогресіями? 2, 4, 8, 16, … 200, 20, 2, … 3, -6, 12, … 1, 4, 16, 64, … 8, 4, 0, -4, … Вказати номер послідовності, яка не є геометричною прогресією. Усні вправи

Знайти невідомі елементи в даній прогресії: (аn) - арифметична прогресія, а1 = 3, а2 = 10. 1) d - ?; 2) a4 - ? (аn) - арифметична прогресія, а1 = 3, d = 2. 3) а7 - ?, 4) а9 -?, 5) а12 - ?. (вn) - геометрична прогресія, в1 = 40, q = . 6) в2 -?, 7) в3 - ?, 8) в4 -?.

bn = b1. qn – 1 Sn = аn = 2n + 1

Шахову гру винайшли в Індії. Ознайомившись з нею, індійський принц Сирам, захоплений дотепністю і різноманітністю можливих ситуацій, покликав до себе її винахідника, ученого Сету, і сказав йому: “Я хочу гідно нагородити тебе, Сета, за прекрасну гру, яку ти придумав. Я досить багатий, і можу виконати будь – яке твоє бажання”.

“Володарю,- відповів Сета,- накажи видати мені за першу клітинку шахівниці одну пшеничну зернину, за другу – дві, за третю – чотири і далі за кожну клітинку вдвічі більше, ніж за попередню .” Принц здивувався, що винахідник так мало запросив. Але обіцянку не зміг виконати. Після ретельних підрахунків вияснилося, що кількість зерен, що бажає одержати Сета, така велика, що її не знайдеться на всьому просторі Землі. Для того, щоб видати нагороду, треба перетворити всі царства в поля, висушити всі річки, озера, розтопити кригу і сніги. Увесь цей простір засіяти пшеницею й усе, що виросте на ньому за 5 років, віддати Сеті. Зі здивуванням слухав принц слова вчених. “Напишіть же мені це дивовижне число,”- сказав він.

Задача 1. (Легенда про винахід шахів) Розв’язання. Маємо геометричну прогресію (вn), в якій в1=1, в2=2, в3= 4…. q = 2. В шахівниці 64 клітинки. Тому S64= 18 446 744 073 709 551 615. Таку кількість зернин можна зібрати з площі, яка приблизно у 2000 разів більша від площі усієї поверхні Землі.

Задача 2 . (Забавна арифметика, 1910 р.) Одного разу розумний бідняк попросив у скупого багатія притулку на 2 тижні на таких умовах: «За це я тобі першого дня заплачу 1 крб., другого – 2 крб., третього 3 крб., збільшуючи щоденну плату на 1 крб. Ти ж будеш давати мені милостиню: Першого дня – 1 коп., другого дня – 2 коп., третього – 4 коп., і т.д. збільшуючи щодня милостиню вдвічі». Багатій з радістю погодився, вважаючи, що умови вигідні для нього. Скільки грошей отримав багатій?

Розв'язання: Сума, яку має сплатити бідняк за 14 днів, складає арифметичну прогресію, в якій а1 = 1 і d =1, S14= 105, тобто 105 крб., а багатій сплачує суму, яка складає суму геометричної прогресії, в якій а1 = 1, q = 2. Тому S14 =214-1= 16383 коп. або 163 крб.83 коп. Отже, багатій, отримавши від бідняка 105 крб., заплатив йому 163 крб.83 коп., тобто, за те, що бідняк у нього проживав 2 неділі, багатій заплатив йому 58 крб.83 коп. (вернувши при цьому і ті гроші, які одержав від бідняка).

Воїну, що служив, дано винагороду: за першу рану –1 коп., за другу – 2 коп., за третю – 4 коп. і т.д. Виявилося, що він одержав винагороду 655руб. 35 коп. Скільки ран було у воїна?

Розв'язання: Маємо геометричну прогресію, в якій в1= 1, в2 = 2, в3 = 4, в4=8 і т.д., q = 2, Sn = 65535. Тоді 1+2+4+ 8+ ….+2n-1 = 65535. 65535 = 2n - 1 = 65535, n = 16. Тобто за такої великодушної системи нагородження воїн повинен одержати 16 ран і залишитися живим, щоб «удостоїтися» винагороди 655руб. 35 коп.

1,3,6,10,15…… 1,4,9,16…n2

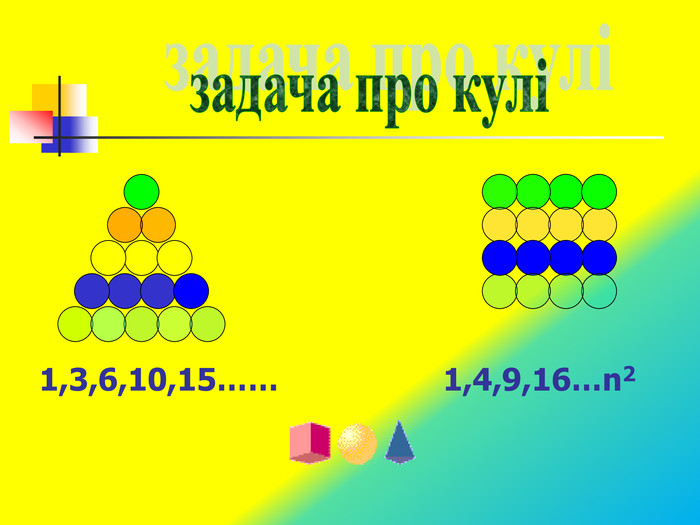
Задача 4. Кулі розміщено у формі трикутника так, що в першому ряду –1 куля, у другому - 2 кулі, у третьому – 3 кулі і т.д. У скільки рядів розміщено кулі, якщо всього їх 120? Розв’язання. Маємо арифметичну прогресію, в якій а1 =1, а2= 2, а3= 3, d = 1, Sn = 120, n - ? Sn = n(n+1) = 2 .120, n2 + n - 240 = 0, n1 = 15, n2=-16 – не задовольняє умови задачі. Тому 120 куль можна розмістити в 15 рядах.

Задача 4. Поливання грядок У городі 30 грядок, кожна довжиною 16м і шириною 2,5м. Поливаючи грядки, городник приносить відра з водою з колодязя, розташованого в 14м від краю городу, і обходить грядки вздовж межі, причому води, принесеної за один раз, вистачає для поливання лише однієї грядки. Якої довжини шлях проходить городник, поливаючи весь город? (Шлях починається і закінчується біля колодязя.)

Розв'язання: Для поливання першої грядки городник проходить шлях 14 + 2,5 + 16 + 2,5 + 16 + 14 = 65 (м). Для поливання другої грядки він проходить шлях 14 + 2,5 + 16 + 2,5 + 16 + 2,5 + 2,5 + 14 = 70 (м). Для кожної наступної грядки потрібно пройти шлях, на 5м довший за попередній. Маємо арифметичну прогресію: 65, 70, 75, … S30 = 30 = 4125 (м). Відповідь: Городник, поливаючи город, проходить шлях 4,125 км.

Трохи гумору Один з учнів, викликаний до дошки, має йти від свого місця до дошки по прямій. Перший крок він робить довжиною 1 м, другий Ѕ м, третій 1/4 м і и т. д. так, що довжина наступного кроку в два рази менша довжини попереднього. Чи дійде учень до дошки, якщо відстань місця учня до дошки по прямій 3 м?

Розв’язок Запишемо послідовність чисел За формулою Маємо Висновок: не дійде! Звідки

Спадщина Джентльмен отримав спадщину. За перший місяць він витратив 100$,а кожного наступного місяця він витрачав на 50$ більше, ніж попередній місяць. Скільки $ він витратив за другий місяць? За третій місяць? Який розмір спадщини, якщо грошей вистачило б на рік такого безбідного життя?

Роз’язання Застосовуємо формлу ,отримуємо Застосував формулу

Задача 6. Бактерія, потрапивши в організм, до кінця 20–ї хвилини ділиться на дві, кожна з них до кінця 20-ї хвилини знов ділиться на дві і т.д. Скільки бактерій стане в організмі через добу? Розв’язання. Маємо геометричну прогресію, в якій в1 = 1, в2 = 2, в3 = 4, q =2 . За добу бактерія поділиться 72 рази (24год.=1440хв., 1440хв : 20хв = 72). Тому S72= бактерій.

Амфітеатр складається з 10 рядів, в кожному наступному ряду на 20 місць більше, ніж у попередньому, а в останньому ряду 280 місць. Скільки людей вміщує амфітеатр? Архітектура

Отже,перед нами арифметична прогресія. Нехай х місць в першому ряду, (х+20) місць в другому ряду, (х+20+20), тобто. (х+40) місць у третьому ряду і т. д. Отже, 100 місць у першому ряду . Відповідь:1900 Розв`язування задачі

При збереженні колод будівельного лісу, їх укладують так ,як показано на малюнку. Скільки колод знаходиться в одній кладці, якщо в її основу покласти 12 колод. Будівництво

Перед нами арифметическая прогрессия: Розв`язування задачі

Задача: Вертикальні стовпи ферми мають такі довжини: найменший 5 дм, а кожний наступний - на 2 дм довший. Знайдіть довжину семи таких стовпів. Роз’язання: Перед нами арифметична прогресія 5, 7, 9, 11, …. Відповідь: 77 дм

Прогресія в літературі Навіть у літературі ми зустрічаємося з математичними поняттями. Згадаємо із “Евгения Онегина”. …Не мог он ямба от хорея, Как мы не бились отличить… Ямб – двоскладова стопа з наголосом на другому складі 2; 4; 6; 8;… Номери наголошених складів утворюють арифметичну прогресію с першим членом 2 та різницею арифметичної прогресії 2. Хорей – двоскладова стопа з наголосом на першому складі. Номера наголошених складів утворюють арифметичну прогресію 1; 3; 5; 7…; Перший член прогресії 1, різниця 2.

Наприклад Ямб “Мой дЯдя сАмых чЕсных прАвил…” Прогресія: 2; 4; 6;…; Хорей “Я пропАл, как звЕрь в загОне” Прогресія: 1; 3; 5;…;

Знайти суму нескінченної геометричної прогресії Розв'язання: В даній нескінченній геометричній прогресії в1 = 1, q = . Тому шукана сума S =

Задача з єгипетського папірусу Розділи 10 мір хліба на 10 чоловік так, щоб кожний одержав на міри більше, ніж попередній. Розв'язання. Треба знайти перші 10 членів арифметичної прогресії (аn ), в якій n=10, Sn=10, d= . Тоді використовуючи формулу суми n перших членів арифметичної прогресії отримуємо звідки і . Тоді

Розв'язування задач І рівень (вn ) - геометрична прогресія, в1 = 3, q = 2. в5 - ? ІІ рівень (вn ) - геометрична прогресія, в2 = 6, в4 = 24, в6 - ? ІІІ рівень Знайти суму 20 перших членів арифметичної прогресії (аn), якщо а7=18,5, а17 = -26,5.

Перевірка результатів І рівень. b5= b1. q4, b5= 3 . 24 = 48, b5= 48. ІІ рівень. b4= b2. q2, q = 2 . b6= b4 . q2, b6= 96 III рівень. а17=а7+10d; d= ; d=-4,5. a7= a1+6d, a1= a7 - 6d, a1= 45,5. S20= = 55, S20=55.

Рефлексія Тест. Результатом своєї роботи вважаю, що я .. А. Разібрався в теорії. В. Навчився розвязувати задачі. С. Повторив весь раніше вивчений матеріал. Що вам не вистачало на уроці при розвязуванні задач? А. Знань. Б. Часу. С. Бажання. Д. Розвязував нормально. Хто допомагав вам в подоланні труднощів на уроці? А. Однокласники. Б. Учитель. С. Підручник. Д. Ніхто.

Задачі на прогресію - це не абстрактні формули. Вони беруться із самого нашого життя, пов’язані з нею і допомагають розв’язувати деякі практичні питання. 

Домашня контрольна робота Завдання середнього рівня 1. Знайдіть суму нескінченної геометричної прогресії: 12; -6; 3. 2. Чому дорівнює сума п'яти перших членів геометричної прогресії, перший член якої b1=6, а знаменник q= 2. 3. Знайдіть перший член арифметичної прогресії, різниця якої дорівнює 15, а сума її перших тринадцяти членів дорівнює 1326. Завдання достатнього рівня 1. Знайдіть суму десяти перших членів арифметичної прогре­сії (an), якщо a6=46, a14=-43. 2. Знайдіть суму чотирьох перших членів геометричної прогресії (bп), якщо b5=16, b8=1024. Завдання високого рівня 1. Знайдіть суму всіх від'ємних членів арифметичної прогресії: -5,2; -4,8; -4,4; ... . 2. Знайдіть перший член і знаменник геометричної прогре­сії (bп), якщо b4-b1=-9, b2+b3+b4=-6.

ПІДСУМКИ «Я сьогодні був вражений.....» « Я вже вмію....» « Ще треба навчитися....»

Досягнення успішного результату під час розв’язання задач – зовсім не привілей математики. Усе людське життя – це не що інше, як постійна постановка та бажання досягти успіху під час розв’язування все нових питань та проблем. Є.Ільєнкова

Дякую за співпрацю і до зустрічі !

Література Програма для загальноосвітніх навчальних закладів. Математика. 5-9 класи.- К.: Ірпінь, 2012. Підручник для 9 кл./За ред. А.Г.Мерзляк,В.Б.Полонський. М.С.Якір.- Харків,Гімназія 2017. Бевз Г.П. Алгебра: Проб. підруч. Для 7-9 кл. – К.:Освіта, 2000. Мальований Ю.І., Литвиненко Г.М., Возняк Г.М. Алгебра: Підруч. для 9 кл. – Тернопіль: навчальна книга - Богдан, 2009. Збірник завдань для державної підсумкової атестації з алгебри. 9 клас/ А.Г.Мерзляк, В.Б .Полонський, М.С.Якір, - Х.:Гімназія, 2017. Журнал « Все для вчителя» № 22-23, 2003. Газета « Математика» № 2, 3 2002; № 2,3 ;2003, № 6, 2004 ; № 2, 14, 2005; № 6 2007.