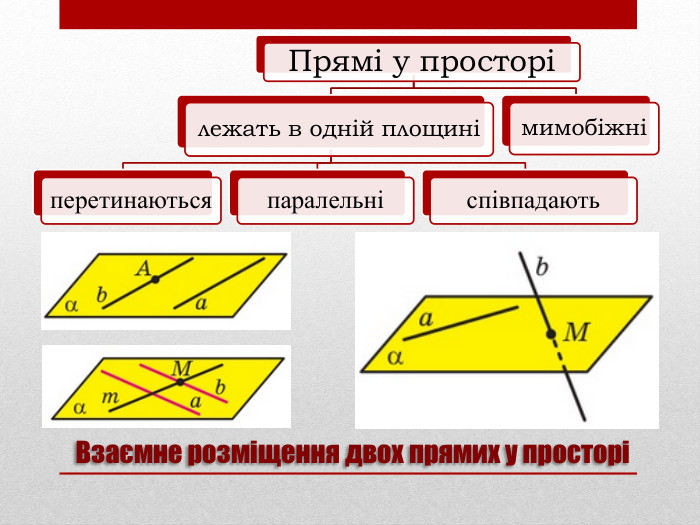
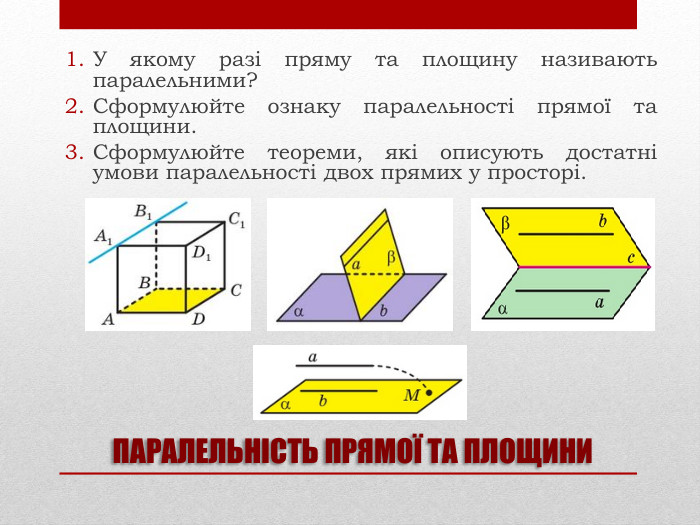
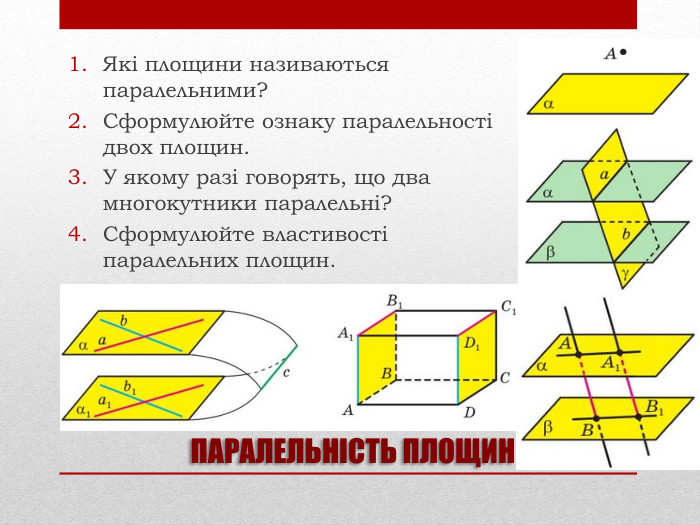
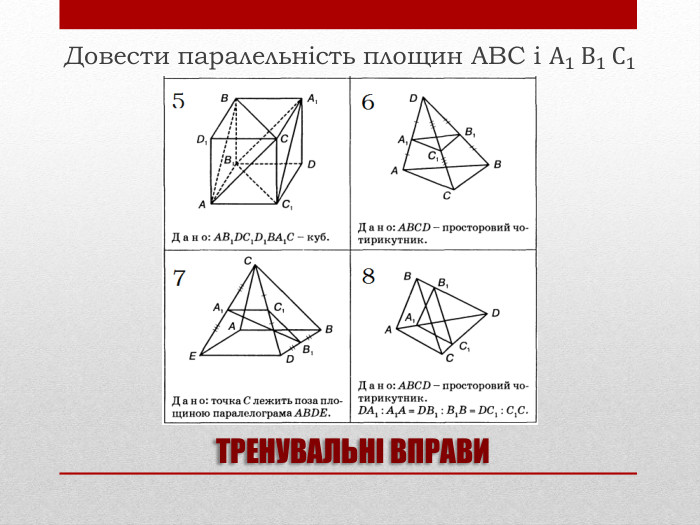
Презентація на тему: "Задачі на паралельність у просторі"
Про матеріал
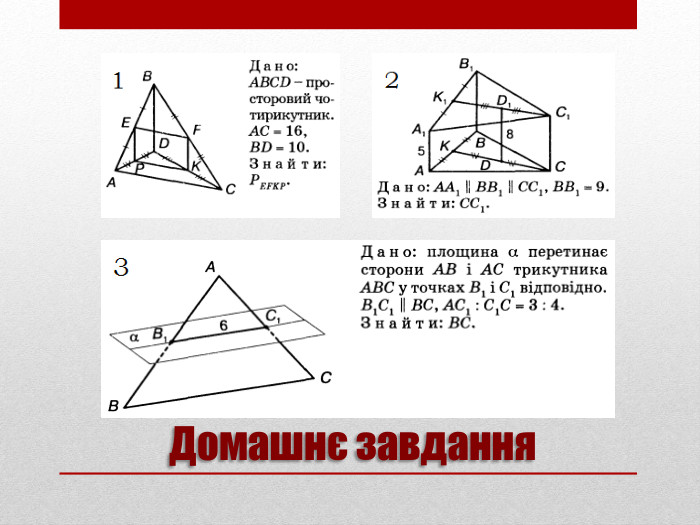
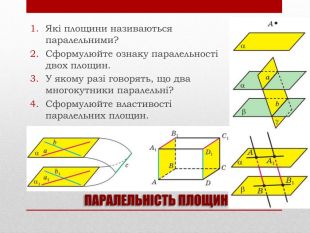
Презентацію "Задачі на паралельність у просторі" доцільно використовувати на занятті математики в 10 класі для узагальнення та систематизації навчального матеріалу. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку