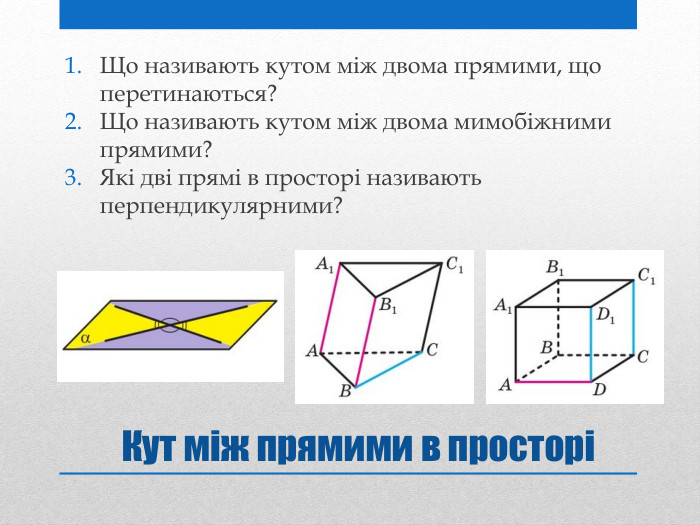
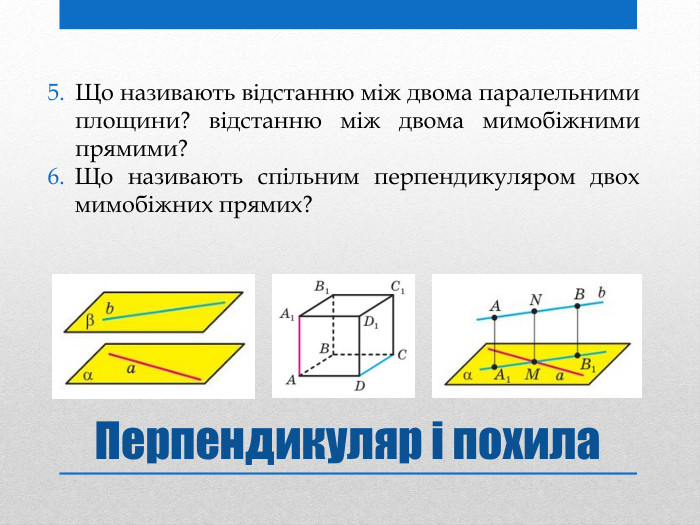
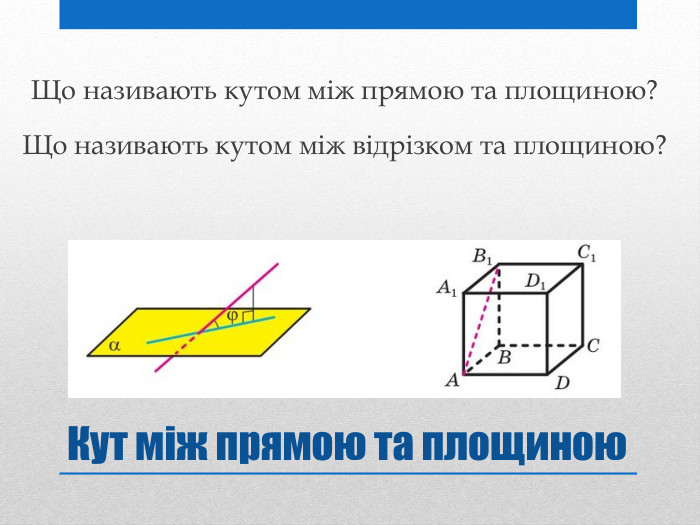
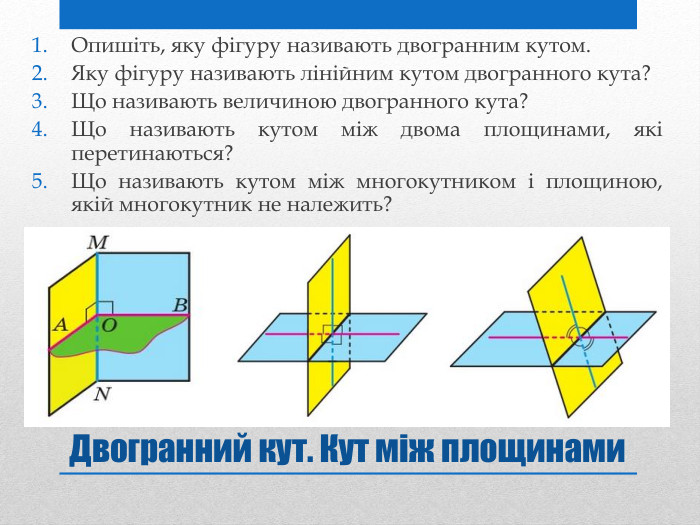
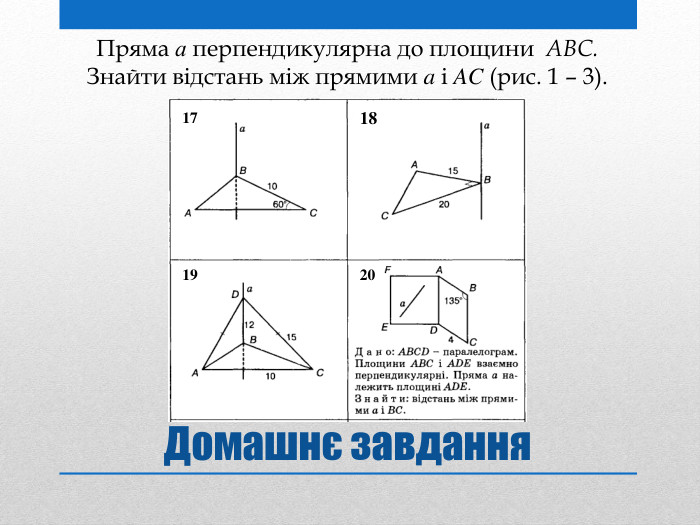
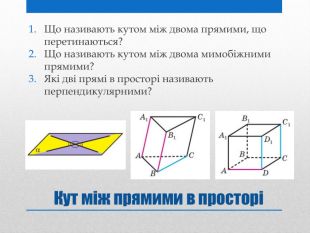
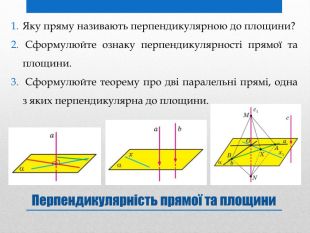
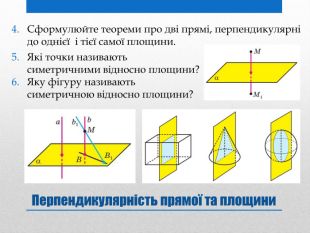
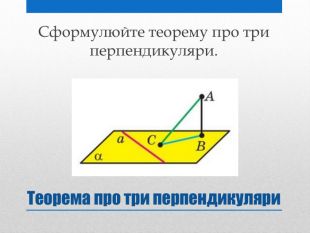
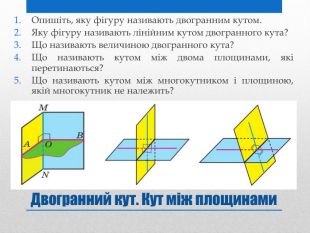
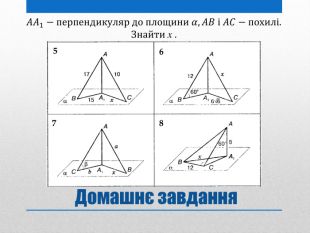
Презентація на тему: "Задачі на перпендикулярність у просторі"
Про матеріал
Презентацію "Задачі на перпендикулярність у просторі" доцільно використовувати на занятті математики в 10 класі для узагальнення та систематизації навчального матеріалу. Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку