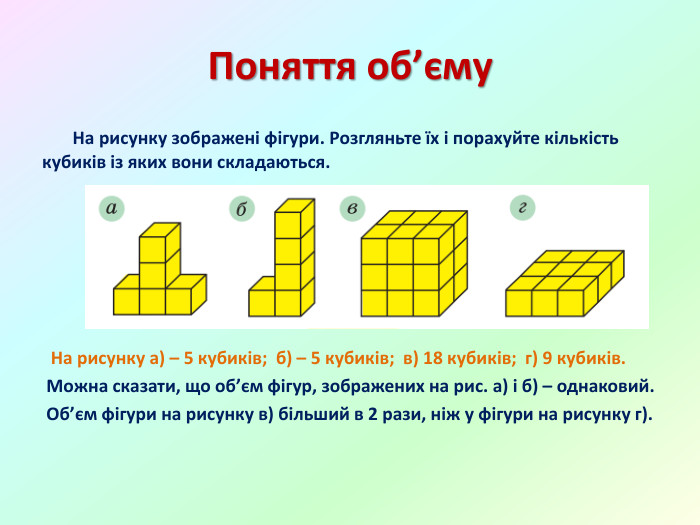
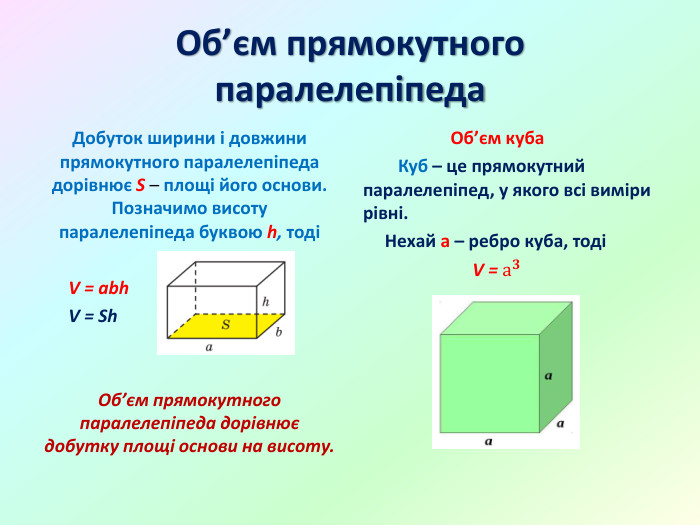
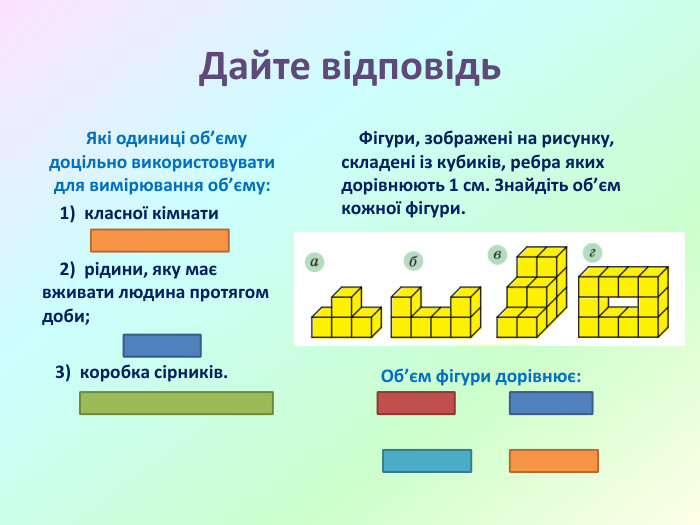
Презентація "Об'єм прямокутного паралелепіпеда"
Про матеріал
Презентація "Об'єм прямокутного паралелепіпеда. Одиниці виміру об'єму" створена для проведення дистанційного уроку математики у 5 класі за програмою НУШ. Підручник "Математика" 5 клас, А.Г.Мерзляк.
Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку