Презентація "Основні поняття стереометрії. Аксіоми стереометрії та наслідки з них. Розміщення прямих у просторі. Ознака паралельності прямих у просторі."
Про матеріал
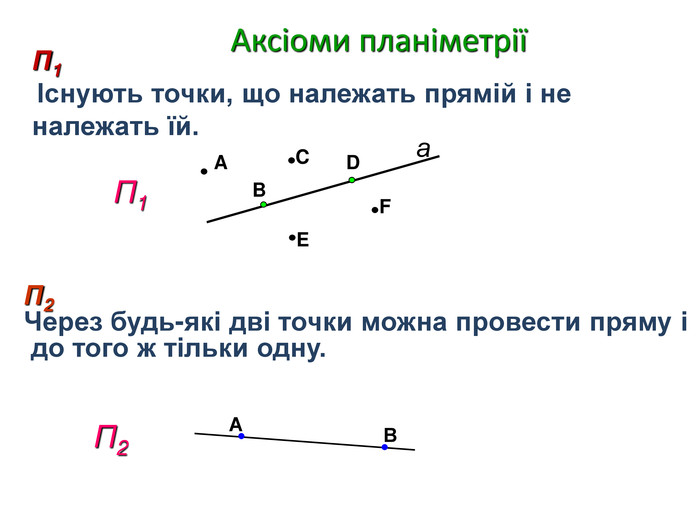
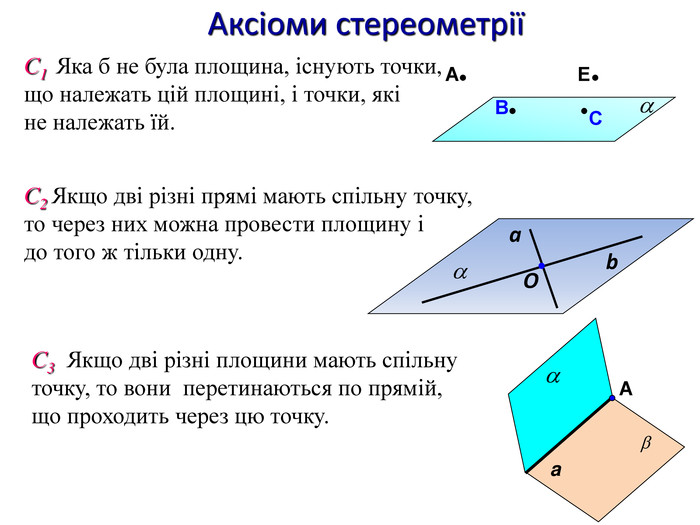
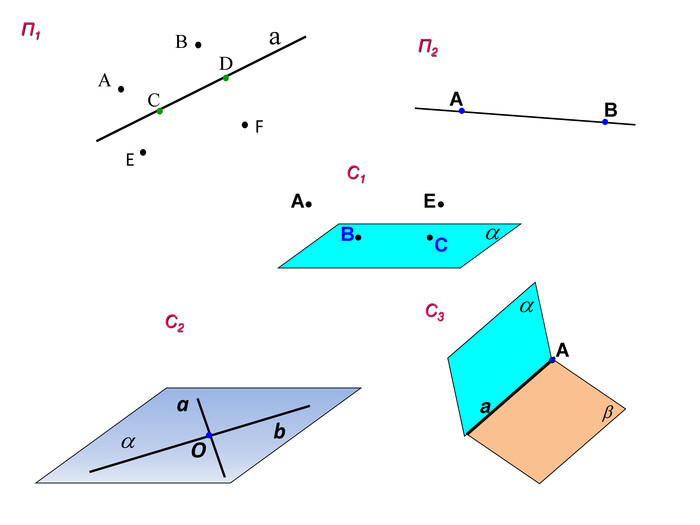
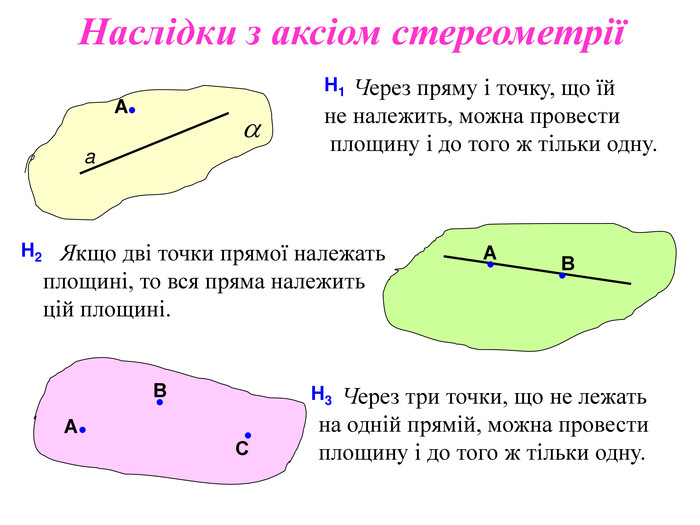
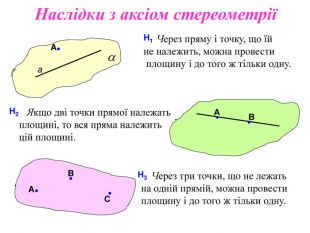
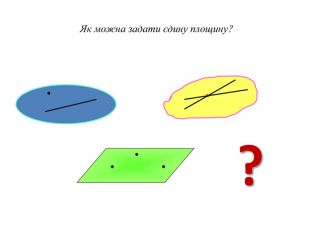
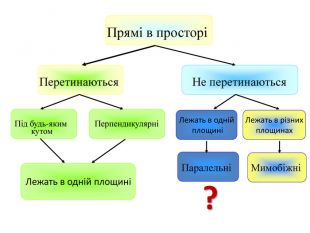
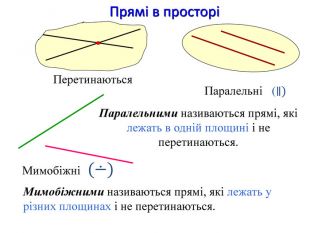
Презентація до першого заняття по стереометрії. При створенні презентації використано підручники: Математика, 10 клас (Бевз) та Геометрія, 10 клас (Біляніна).
Перегляд файлу
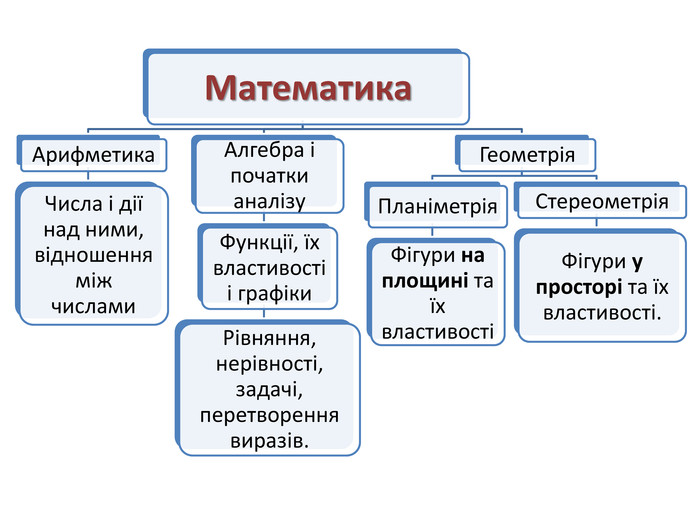
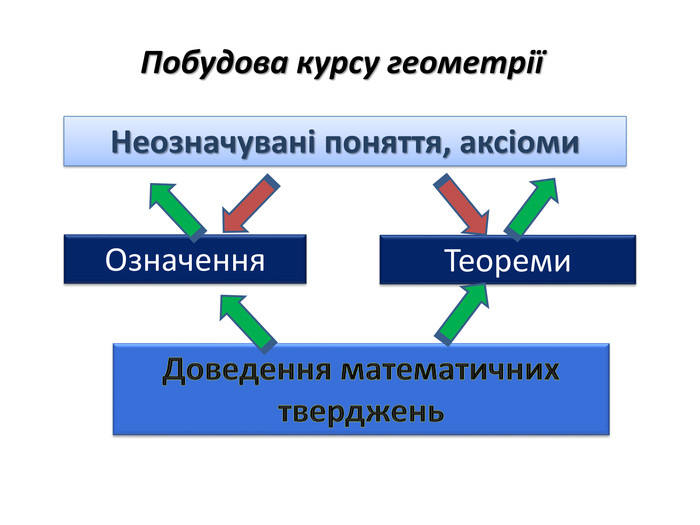
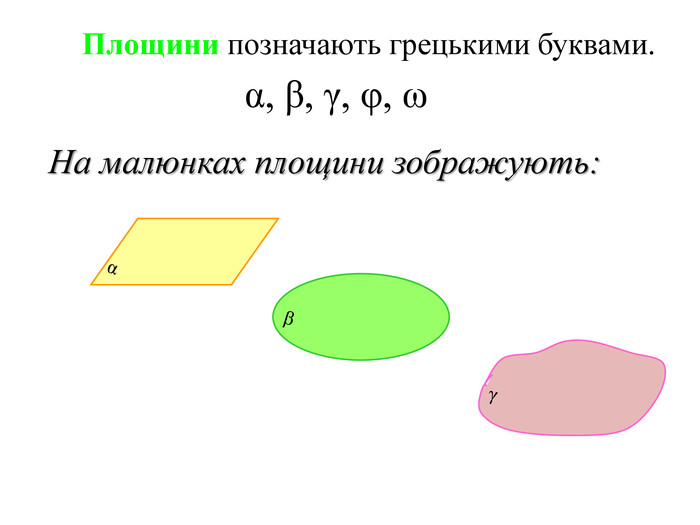
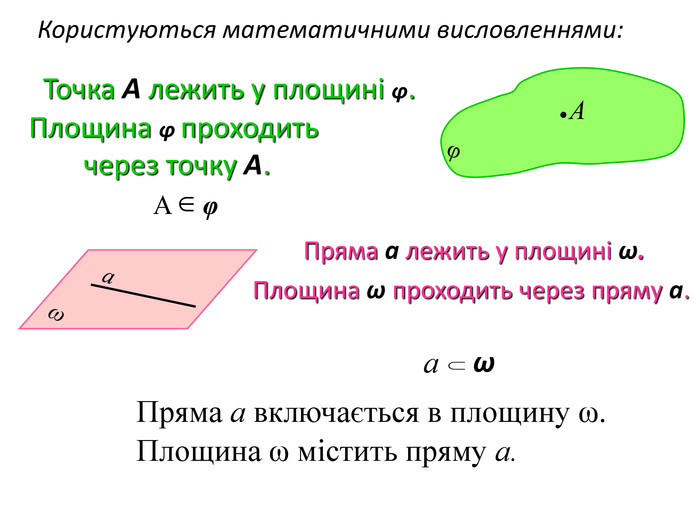
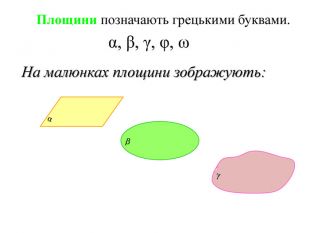
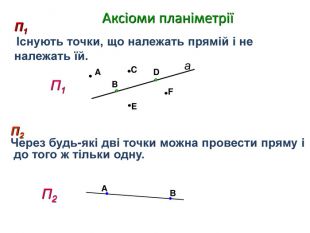
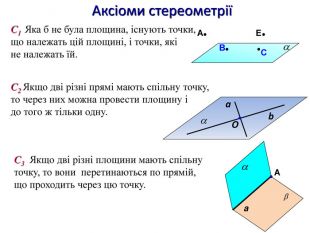
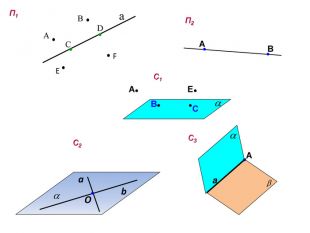
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
pptx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку


















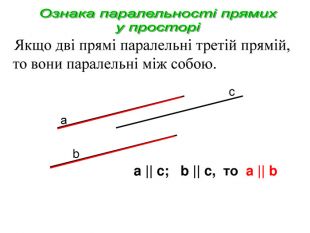
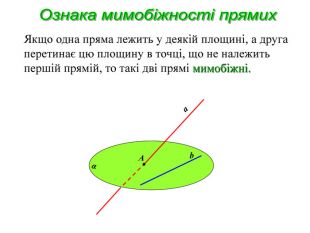
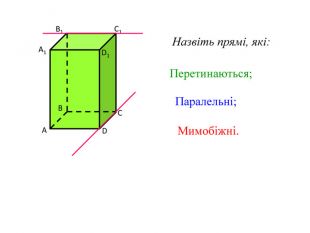


-

Приходько Наталія Михайлівна
13.09.2023 в 18:59
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Kлачик Альона Ярославівна
10.09.2023 в 08:58
Чітко, структуровано, гарно оформлено. Дуже змістовна презентація. Дякую за можливість скористатися.
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Константинова Олена Павлівна
22.09.2022 в 20:00
Загальна:
5.0
Структурованість
5.0
Оригінальність викладу
5.0
Відповідність темі
5.0
-

Нижборська Наталія
31.10.2020 в 20:00
Загальна:
3.3
Структурованість
3.0
Оригінальність викладу
3.0
Відповідність темі
4.0
-

Таранчук Оксана Григорівна
14.10.2020 в 23:27
Загальна:
4.0
Структурованість
4.0
Оригінальність викладу
4.0
Відповідність темі
4.0
-

Шкатула Лариса Павлівна
10.10.2020 в 09:07
Загальна:
3.0
Структурованість
3.0
Оригінальність викладу
3.0
Відповідність темі
3.0
Показати ще 3 відгука