Презентація "Основні задачі на розв'язування трикутників"
Про матеріал
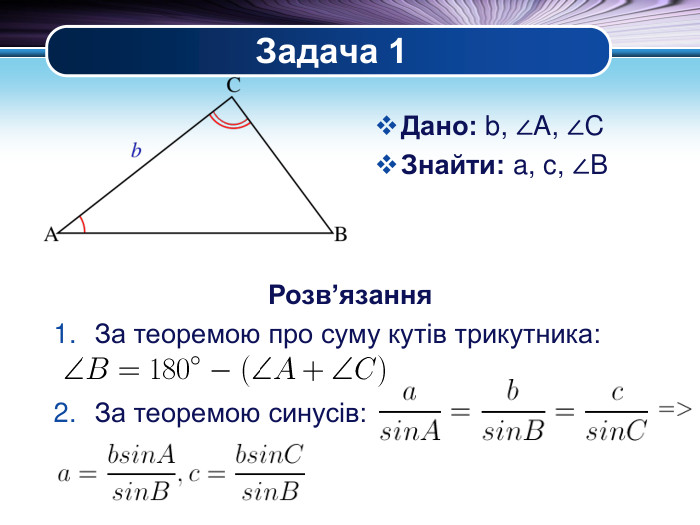
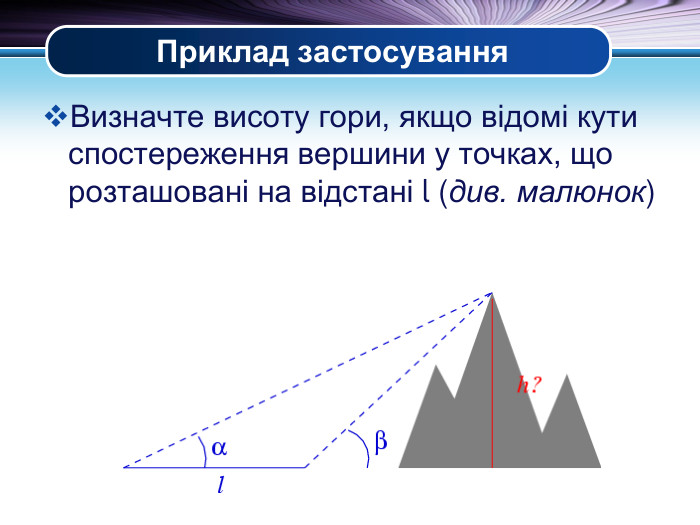
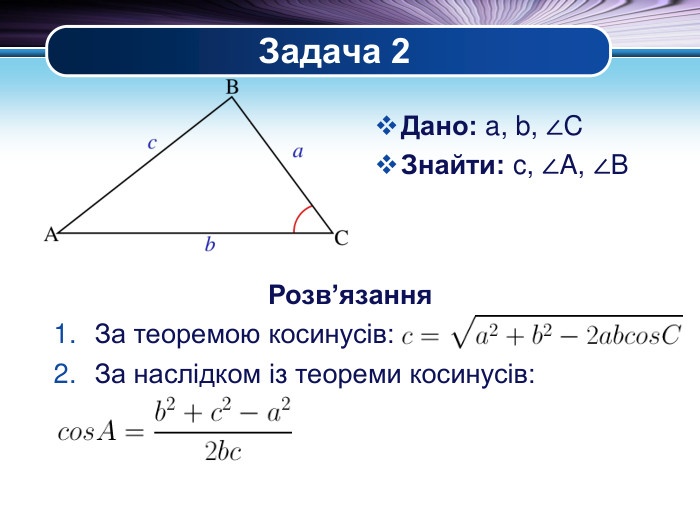
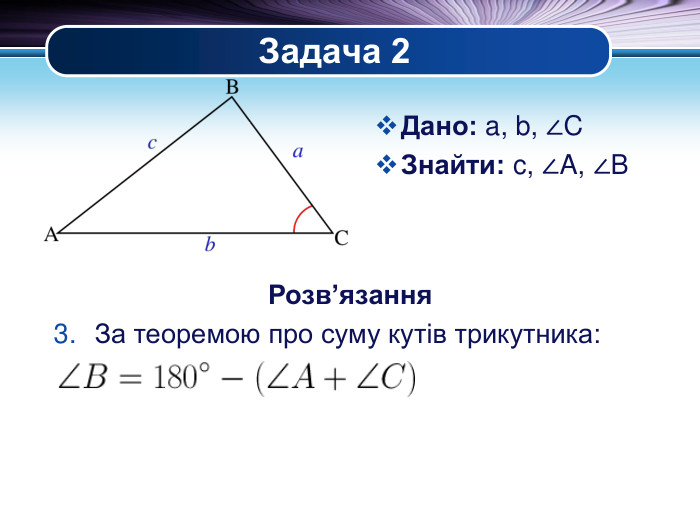
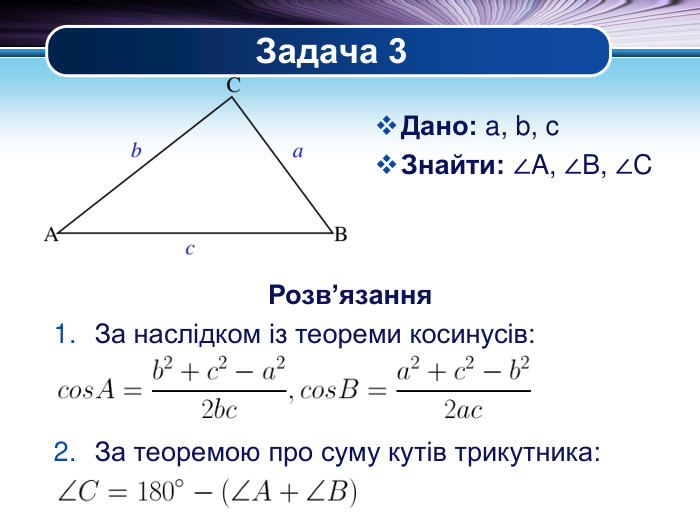
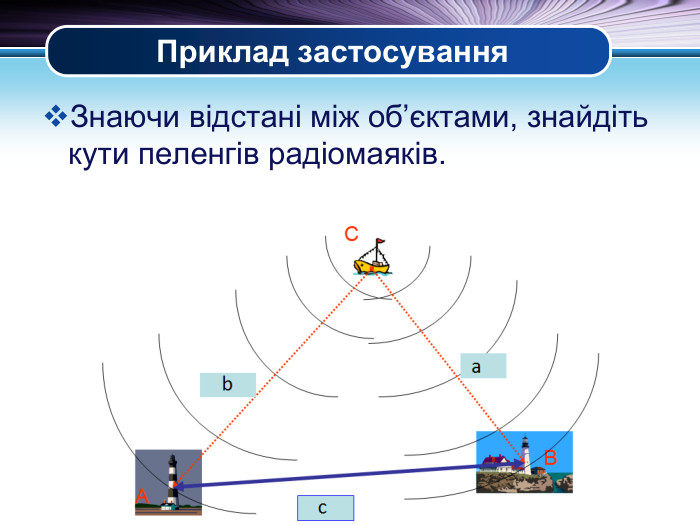
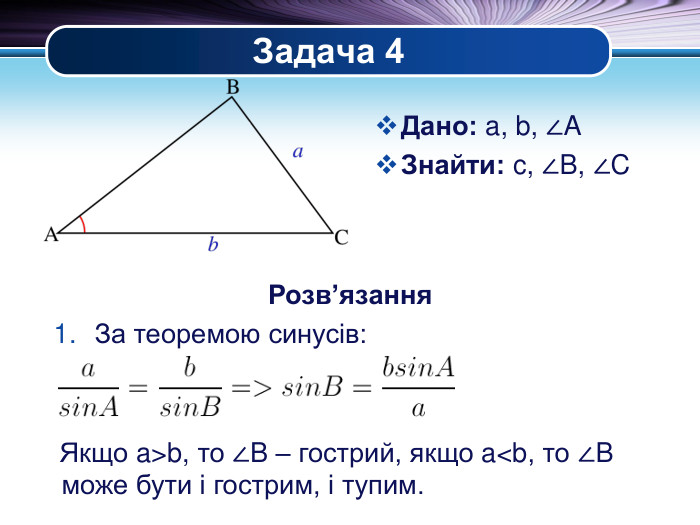
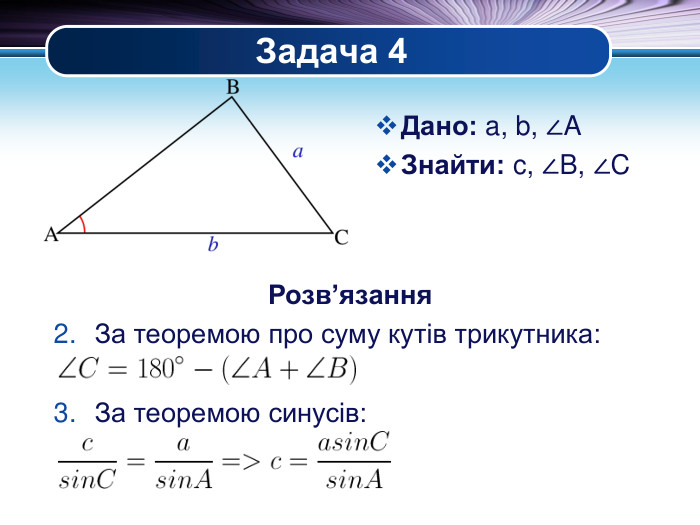
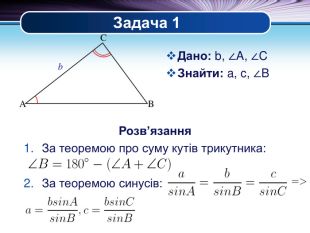
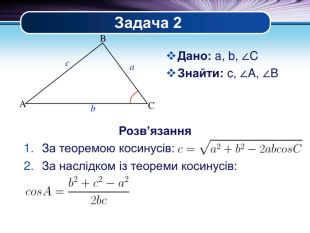
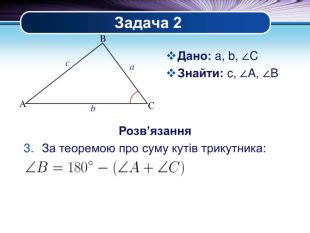
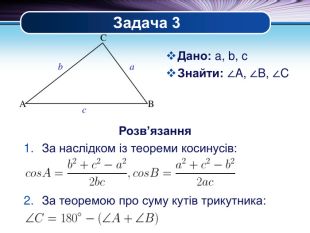
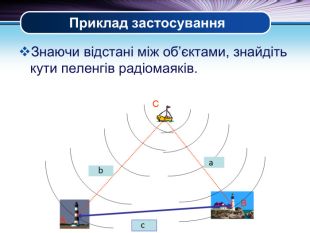
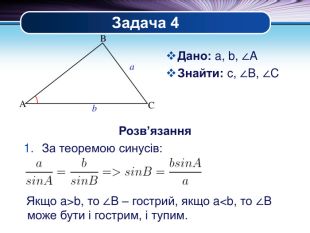
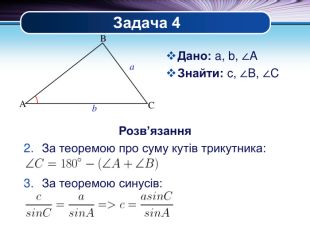
Презентація "Основні задачі на розв'язування трикутників" може бути корисною під час уроків повторення теми у 9 класі. В ній наведено теореми синусів та теореми косинусів для розв'язування трикутників, та зразки застосування цих теорем для задач практичного змісту Перегляд файлу
Зміст слайдів
Середня оцінка розробки
Оцінки та відгуки
ppt
До підручника
Геометрія 9 клас (Мерзляк А. Г., Полонський В. Б., Якір М. С)
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку